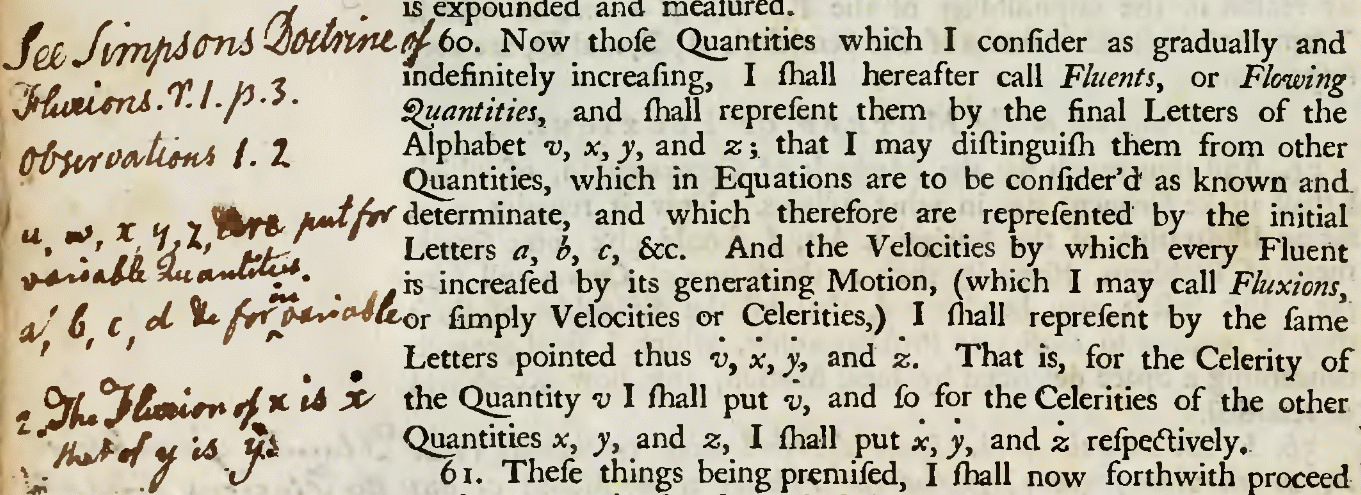|
Fluxion (mathematics)
A fluxion is the instantaneous rate of change, or gradient, of a fluent (mathematics), fluent (a time-varying quantity, or function (mathematics), function) at a given point. Fluxions were introduced by Isaac Newton to describe his form of a time derivative (a derivative with respect to time). Newton introduced the concept in 1665 and detailed them in his mathematics, mathematical treatise, ''Method of Fluxions''. Fluxions and fluents made up Newton's early calculus. History Fluxions were central to the Leibniz–Newton calculus controversy, when Newton sent a letter to Gottfried Wilhelm Leibniz explaining them, but concealing his words in code due to his suspicion. He wrote: The gibberish string was in fact a hash code (by denoting the frequency of each letter) of the Latin phrase ''Data æqvatione qvotcvnqve flventes qvantitates involvente, flvxiones invenire: et vice versa'', meaning: "Given an equation that consists of any number of flowing quantities, to find the fluxions: ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
The Method Of Fluxions And Infinite Series P
''The'' is a grammatical Article (grammar), article in English language, English, denoting nouns that are already or about to be mentioned, under discussion, implied or otherwise presumed familiar to listeners, readers, or speakers. It is the definite article in English. ''The'' is the Most common words in English, most frequently used word in the English language; studies and analyses of texts have found it to account for seven percent of all printed English-language words. It is derived from gendered articles in Old English which combined in Middle English and now has a single form used with nouns of any gender. The word can be used with both singular and plural nouns, and with a noun that starts with any letter. This is different from many other languages, which have different forms of the definite article for different genders or numbers. Pronunciation In most dialects, "the" is pronounced as (with the voiced dental fricative followed by a schwa) when followed by a con ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Infinitesimal
In mathematics, an infinitesimal number is a non-zero quantity that is closer to 0 than any non-zero real number is. The word ''infinitesimal'' comes from a 17th-century Modern Latin coinage ''infinitesimus'', which originally referred to the "infinity- th" item in a sequence. Infinitesimals do not exist in the standard real number system, but they do exist in other number systems, such as the surreal number system and the hyperreal number system, which can be thought of as the real numbers augmented with both infinitesimal and infinite quantities; the augmentations are the reciprocals of one another. Infinitesimal numbers were introduced in the development of calculus, in which the derivative was first conceived as a ratio of two infinitesimal quantities. This definition was not rigorously formalized. As calculus developed further, infinitesimals were replaced by limits, which can be calculated using the standard real numbers. In the 3rd century BC Archimedes used what ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Analysis
Analysis is the branch of mathematics dealing with continuous functions, limit (mathematics), limits, and related theories, such as Derivative, differentiation, Integral, integration, measure (mathematics), measure, infinite sequences, series (mathematics), series, and analytic functions. These theories are usually studied in the context of Real number, real and Complex number, complex numbers and Function (mathematics), functions. Analysis evolved from calculus, which involves the elementary concepts and techniques of analysis. Analysis may be distinguished from geometry; however, it can be applied to any Space (mathematics), space of mathematical objects that has a definition of nearness (a topological space) or specific distances between objects (a metric space). History Ancient Mathematical analysis formally developed in the 17th century during the Scientific Revolution, but many of its ideas can be traced back to earlier mathematicians. Early results in analysis were ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nonstandard Analysis
The history of calculus is fraught with philosophical debates about the meaning and logical validity of fluxions or infinitesimal numbers. The standard way to resolve these debates is to define the operations of calculus using (ε, δ)-definition of limit, limits rather than infinitesimals. Nonstandard analysis instead reformulates the calculus using a logically rigorous notion of infinitesimal numbers. Nonstandard analysis originated in the early 1960s by the mathematician Abraham Robinson. He wrote: ... the idea of infinitely small or ''infinitesimal'' quantities seems to appeal naturally to our intuition. At any rate, the use of infinitesimals was widespread during the formative stages of the Differential and Integral Calculus. As for the objection ... that the distance between two distinct real numbers cannot be infinitely small, Gottfried Wilhelm Leibniz argued that the theory of infinitesimals implies the introduction of ideal numbers which might be infinitely small or inf ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperreal Number
In mathematics, hyperreal numbers are an extension of the real numbers to include certain classes of infinite and infinitesimal numbers. A hyperreal number x is said to be finite if, and only if, , x, [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Newton's Notation
In differential calculus, there is no single standard notation for differentiation. Instead, several notations for the derivative of a function or a dependent variable have been proposed by various mathematicians, including Leibniz, Newton, Lagrange, and Arbogast. The usefulness of each notation depends on the context in which it is used, and it is sometimes advantageous to use more than one notation in a given context. For more specialized settings—such as partial derivatives in multivariable calculus, tensor analysis, or vector calculus—other notations, such as subscript notation or the ∇ operator are common. The most common notations for differentiation (and its opposite operation, antidifferentiation or indefinite integration) are listed below. Leibniz's notation The original notation employed by Gottfried Leibniz is used throughout mathematics. It is particularly common when the equation is regarded as a functional relationship between dependent and independe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
History Of Calculus
Calculus, originally called infinitesimal calculus, is a mathematical discipline focused on limits, continuity, derivatives, integrals, and infinite series. Many elements of calculus appeared in ancient Greece, then in China and the Middle East, and still later again in medieval Europe and in India. Infinitesimal calculus was developed in the late 17th century by Isaac Newton and Gottfried Wilhelm Leibniz independently of each other. An argument over priority led to the Leibniz–Newton calculus controversy which continued until the death of Leibniz in 1716. The development of calculus and its uses within the sciences have continued to the present. Etymology In mathematics education, ''calculus'' denotes courses of elementary mathematical analysis, which are mainly devoted to the study of functions and limits. The word ''calculus'' is Latin for "small pebble" (the diminutive of '' calx,'' meaning "stone"), a meaning which still persists in medicine. Because such pebbles were ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Leibniz's Notation
In calculus, Leibniz's notation, named in honor of the 17th-century German philosopher and mathematician Gottfried Wilhelm Leibniz, uses the symbols and to represent infinitely small (or infinitesimal) increments of and , respectively, just as and represent finite increments of and , respectively. Consider as a function of a variable , or = . If this is the case, then the derivative of with respect to , which later came to be viewed as the limit :\lim_\frac = \lim_\frac, was, according to Leibniz, the quotient of an infinitesimal increment of by an infinitesimal increment of , or :\frac=f'(x), where the right hand side is Joseph-Louis Lagrange's notation for the derivative of at . The infinitesimal increments are called . Related to this is the integral in which the infinitesimal increments are summed (e.g. to compute lengths, areas and volumes as sums of tiny pieces), for which Leibniz also supplied a closely related notation involving the same differentials ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Limit (mathematics)
In mathematics, a limit is the value that a function (or sequence) approaches as the argument (or index) approaches some value. Limits of functions are essential to calculus and mathematical analysis, and are used to define continuity, derivatives, and integrals. The concept of a limit of a sequence is further generalized to the concept of a limit of a topological net, and is closely related to limit and direct limit in category theory. The limit inferior and limit superior provide generalizations of the concept of a limit which are particularly relevant when the limit at a point may not exist. Notation In formulas, a limit of a function is usually written as : \lim_ f(x) = L, and is read as "the limit of of as approaches equals ". This means that the value of the function can be made arbitrarily close to , by choosing sufficiently close to . Alternatively, the fact that a function approaches the limit as approaches is sometimes denoted by a right arrow (→ or ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Zero
0 (zero) is a number representing an empty quantity. Adding (or subtracting) 0 to any number leaves that number unchanged; in mathematical terminology, 0 is the additive identity of the integers, rational numbers, real numbers, and complex numbers, as well as other algebraic structures. Multiplying any number by 0 results in 0, and consequently division by zero has no meaning in arithmetic. As a numerical digit, 0 plays a crucial role in decimal notation: it indicates that the power of ten corresponding to the place containing a 0 does not contribute to the total. For example, "205" in decimal means two hundreds, no tens, and five ones. The same principle applies in place-value notations that uses a base other than ten, such as binary and hexadecimal. The modern use of 0 in this manner derives from Indian mathematics that was transmitted to Europe via medieval Islamic mathematicians and popularized by Fibonacci. It was independently used by the Maya. Common name ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Division By Zero
In mathematics, division by zero, division (mathematics), division where the divisor (denominator) is 0, zero, is a unique and problematic special case. Using fraction notation, the general example can be written as \tfrac a0, where a is the dividend (numerator). The usual definition of the quotient in elementary arithmetic is the number which yields the dividend when multiplication, multiplied by the divisor. That is, c = \tfrac ab is equivalent to c \cdot b = a. By this definition, the quotient q = \tfrac is nonsensical, as the product q \cdot 0 is always 0 rather than some other number a. Following the ordinary rules of elementary algebra while allowing division by zero can create a mathematical fallacy, a subtle mistake leading to absurd results. To prevent this, the arithmetic of real numbers and more general numerical structures called field (mathematics), fields leaves division by zero undefined (mathematics), undefined, and situations where division by zero might occur m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
The Analyst
''The Analyst'' (subtitled ''A Discourse Addressed to an Infidel Mathematician: Wherein It Is Examined Whether the Object, Principles, and Inferences of the Modern Analysis Are More Distinctly Conceived, or More Evidently Deduced, Than Religious Mysteries and Points of Faith'') is a book by George Berkeley. It was first published in 1734, first by J. Tonson (London), then by S. Fuller (Dublin). The "infidel mathematician" is believed to have been Edmond Halley, though others have speculated Sir Isaac Newton was intended. The book contains a direct attack on the foundations of calculus, specifically on Isaac Newton's notion of Method of Fluxions, fluxions and on Gottfried Leibniz, Leibniz's notion of infinitesimal change. Background and purpose From his earliest days as a writer, Berkeley had taken up his satirical pen to attack what were then called 'free-thinkers' (secularists, sceptics, agnostics, atheists, etc.—in short, anyone who doubted the truths of received Christi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |