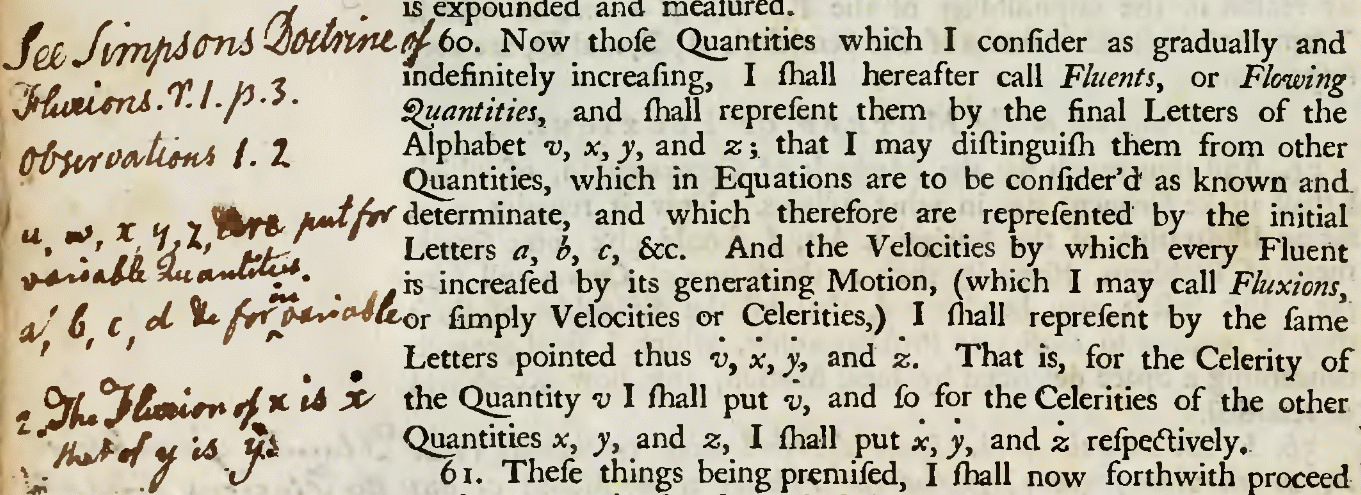 |
Fluent (mathematics)
A fluent is a time-varying quantity or variable. The term was used by Isaac Newton in his early calculus to describe his form of a function. The concept was introduced by Newton in 1665 and detailed in his mathematical treatise, ''Method of Fluxions''. Newton described any variable that changed its value as a fluent – for example, the velocity of a ball thrown in the air. The derivative of a fluent is known as a fluxion, the main focus of Newton's calculus. A fluent can be found from its corresponding fluxion through integration. See also *''Method of Fluxions'' *History of calculus *Leibniz–Newton calculus controversy *Derivative *Newton's notation *Fluxion A fluxion is the instantaneous rate of change, or gradient, of a fluent (a time-varying quantity, or function) at a given point. Fluxions were introduced by Isaac Newton to describe his form of a time derivative (a derivative with respect to t ... References {{Isaac Newton, state=collapsed Mathematical an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
The Method Of Fluxions And Infinite Series P
''The'' is a grammatical Article (grammar), article in English language, English, denoting nouns that are already or about to be mentioned, under discussion, implied or otherwise presumed familiar to listeners, readers, or speakers. It is the definite article in English. ''The'' is the Most common words in English, most frequently used word in the English language; studies and analyses of texts have found it to account for seven percent of all printed English-language words. It is derived from gendered articles in Old English which combined in Middle English and now has a single form used with nouns of any gender. The word can be used with both singular and plural nouns, and with a noun that starts with any letter. This is different from many other languages, which have different forms of the definite article for different genders or numbers. Pronunciation In most dialects, "the" is pronounced as (with the voiced dental fricative followed by a schwa) when followed by a con ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
 |
Variable (mathematics)
In mathematics, a variable (from Latin language, Latin ) is a Mathematical symbol, symbol, typically a letter, that refers to an unspecified mathematical object. One says colloquially that the variable ''represents'' or ''denotes'' the object, and that any valid candidate for the object is the value (mathematics), value of the variable. The values a variable can take are usually of the same kind, often numbers. More specifically, the values involved may form a Set (mathematics), set, such as the set of real numbers. The object may not always exist, or it might be uncertain whether any valid candidate exists or not. For example, one could represent two integers by the variables and and require that the value of the square of is twice the square of , which in algebraic notation can be written . A definitive proof that this relationship is impossible to satisfy when and are restricted to integer numbers isn't obvious, but it has been known since ancient times and has had a big ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
 |
Isaac Newton
Sir Isaac Newton () was an English polymath active as a mathematician, physicist, astronomer, alchemist, theologian, and author. Newton was a key figure in the Scientific Revolution and the Age of Enlightenment, Enlightenment that followed. His book (''Mathematical Principles of Natural Philosophy''), first published in 1687, achieved the Unification of theories in physics#Unification of gravity and astronomy, first great unification in physics and established classical mechanics. Newton also made seminal contributions to optics, and Leibniz–Newton calculus controversy, shares credit with German mathematician Gottfried Wilhelm Leibniz for formulating calculus, infinitesimal calculus, though he developed calculus years before Leibniz. Newton contributed to and refined the scientific method, and his work is considered the most influential in bringing forth modern science. In the , Newton formulated the Newton's laws of motion, laws of motion and Newton's law of universal g ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
Calculus
Calculus is the mathematics, mathematical study of continuous change, in the same way that geometry is the study of shape, and algebra is the study of generalizations of arithmetic operations. Originally called infinitesimal calculus or "the calculus of infinitesimals", it has two major branches, differential calculus and integral calculus. The former concerns instantaneous Rate of change (mathematics), rates of change, and the slopes of curves, while the latter concerns accumulation of quantities, and areas under or between curves. These two branches are related to each other by the fundamental theorem of calculus. They make use of the fundamental notions of convergence (mathematics), convergence of infinite sequences and Series (mathematics), infinite series to a well-defined limit (mathematics), limit. It is the "mathematical backbone" for dealing with problems where variables change with time or another reference variable. Infinitesimal calculus was formulated separately ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Function (mathematics)
In mathematics, a function from a set (mathematics), set to a set assigns to each element of exactly one element of .; the words ''map'', ''mapping'', ''transformation'', ''correspondence'', and ''operator'' are sometimes used synonymously. The set is called the Domain of a function, domain of the function and the set is called the codomain of the function. Functions were originally the idealization of how a varying quantity depends on another quantity. For example, the position of a planet is a ''function'' of time. History of the function concept, Historically, the concept was elaborated with the infinitesimal calculus at the end of the 17th century, and, until the 19th century, the functions that were considered were differentiable function, differentiable (that is, they had a high degree of regularity). The concept of a function was formalized at the end of the 19th century in terms of set theory, and this greatly increased the possible applications of the concept. A f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
 |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
Method Of Fluxions
''Method of Fluxions'' () is a mathematical treatise by Sir Isaac Newton which served as the earliest written formulation of modern calculus. The book was completed in 1671 and posthumously published in 1736. Background Fluxion is Newton's term for a derivative. He originally developed the method at Woolsthorpe Manor during the closing of Cambridge due to the Great Plague of London from 1665 to 1667. Newton did not choose to make his findings known (similarly, his findings which eventually became the '' Philosophiae Naturalis Principia Mathematica'' were developed at this time and hidden from the world in Newton's notes for many years). Gottfried Leibniz developed his form of calculus independently around 1673, seven years after Newton had developed the basis for differential calculus, as seen in surviving documents like “the method of fluxions and fluents..." from 1666. Leibniz, however, published his discovery of differential calculus in 1684, nine years before Newton forma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Fluxion
A fluxion is the instantaneous rate of change, or gradient, of a fluent (a time-varying quantity, or function) at a given point. Fluxions were introduced by Isaac Newton to describe his form of a time derivative (a derivative with respect to time). Newton introduced the concept in 1665 and detailed them in his mathematical treatise, '' Method of Fluxions''. Fluxions and fluents made up Newton's early calculus. History Fluxions were central to the Leibniz–Newton calculus controversy, when Newton sent a letter to Gottfried Wilhelm Leibniz explaining them, but concealing his words in code due to his suspicion. He wrote: The gibberish string was in fact a hash code (by denoting the frequency of each letter) of the Latin phrase ''Data æqvatione qvotcvnqve flventes qvantitates involvente, flvxiones invenire: et vice versa'', meaning: "Given an equation that consists of any number of flowing quantities, to find the fluxions: and vice versa". Example If the fluent is defined as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Integral
In mathematics, an integral is the continuous analog of a Summation, sum, which is used to calculate area, areas, volume, volumes, and their generalizations. Integration, the process of computing an integral, is one of the two fundamental operations of calculus,Integral calculus is a very well established mathematical discipline for which there are many sources. See and , for example. the other being Derivative, differentiation. Integration was initially used to solve problems in mathematics and physics, such as finding the area under a curve, or determining displacement from velocity. Usage of integration expanded to a wide variety of scientific fields thereafter. A definite integral computes the signed area of the region in the plane that is bounded by the Graph of a function, graph of a given Function (mathematics), function between two points in the real line. Conventionally, areas above the horizontal Coordinate axis, axis of the plane are positive while areas below are n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
 |
History Of Calculus
Calculus, originally called infinitesimal calculus, is a mathematical discipline focused on limits, continuity, derivatives, integrals, and infinite series. Many elements of calculus appeared in ancient Greece, then in China and the Middle East, and still later again in medieval Europe and in India. Infinitesimal calculus was developed in the late 17th century by Isaac Newton and Gottfried Wilhelm Leibniz independently of each other. An argument over priority led to the Leibniz–Newton calculus controversy which continued until the death of Leibniz in 1716. The development of calculus and its uses within the sciences have continued to the present. Etymology In mathematics education, ''calculus'' denotes courses of elementary mathematical analysis, which are mainly devoted to the study of functions and limits. The word ''calculus'' is Latin for "small pebble" (the diminutive of '' calx,'' meaning "stone"), a meaning which still persists in medicine. Because such pebbles were ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
 |
Leibniz–Newton Calculus Controversy
In the history of calculus, the calculus controversy () was an argument between mathematicians Isaac Newton and Gottfried Wilhelm Leibniz over who had first discovered calculus. The question was a major intellectual controversy, beginning in 1699 and reaching its peak in 1712. Leibniz had published his work on calculus first, but Newton's supporters accused Leibniz of plagiarizing Newton's unpublished ideas. The modern consensus is that the two men independently developed their ideas. Their creation of calculus has been called "the greatest advance in mathematics that had taken place since the time of Archimedes." Newton stated he had begun working on a form of calculus (which he called " The Method of Fluxions and Infinite Series") in 1666, at the age of 23, but did not publish it until 1737 as a minor annotation in the back of one of his works decades later (a relevant Newton manuscript of October 1666 is now published among his mathematical papers). Gottfried Leibniz began wo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
Derivative
In mathematics, the derivative is a fundamental tool that quantifies the sensitivity to change of a function's output with respect to its input. The derivative of a function of a single variable at a chosen input value, when it exists, is the slope of the tangent line to the graph of the function at that point. The tangent line is the best linear approximation of the function near that input value. For this reason, the derivative is often described as the instantaneous rate of change, the ratio of the instantaneous change in the dependent variable to that of the independent variable. The process of finding a derivative is called differentiation. There are multiple different notations for differentiation. '' Leibniz notation'', named after Gottfried Wilhelm Leibniz, is represented as the ratio of two differentials, whereas ''prime notation'' is written by adding a prime mark. Higher order notations represent repeated differentiation, and they are usually denoted in Leib ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |