Euclidean Traveling Salesman on:
[Wikipedia]
[Google]
[Amazon]

 In the theory of computational complexity, the travelling salesman problem (TSP) asks the following question: "Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city exactly once and returns to the origin city?" It is an
In the theory of computational complexity, the travelling salesman problem (TSP) asks the following question: "Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city exactly once and returns to the origin city?" It is an
 The TSP was mathematically formulated in the 19th century by the Irish mathematician
The TSP was mathematically formulated in the 19th century by the Irish mathematician
 TSP can be modeled as an undirected weighted graph, such that cities are the graph's vertices, paths are the graph's edges, and a path's distance is the edge's weight. It is a minimization problem starting and finishing at a specified vertex after having visited each other vertex exactly once. Often, the model is a
TSP can be modeled as an undirected weighted graph, such that cities are the graph's vertices, paths are the graph's edges, and a path's distance is the edge's weight. It is a minimization problem starting and finishing at a specified vertex after having visited each other vertex exactly once. Often, the model is a
 Improving these time bounds seems to be difficult. For example, it has not been determined whether a classical
Improving these time bounds seems to be difficult. For example, it has not been determined whether a classical 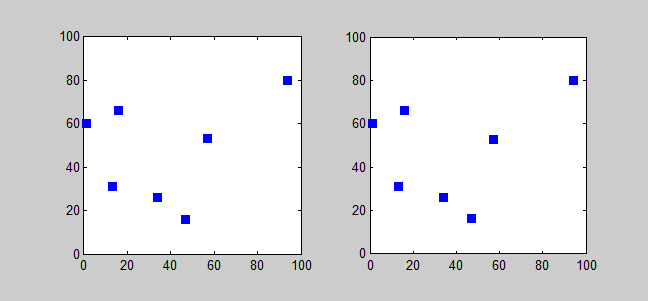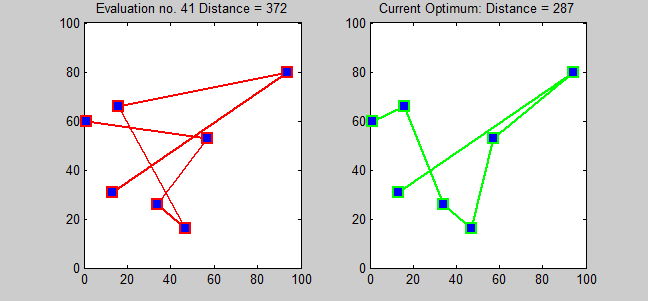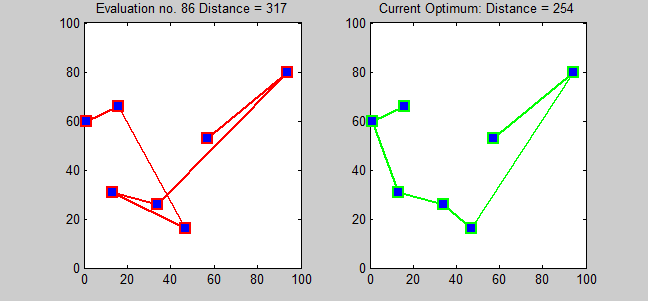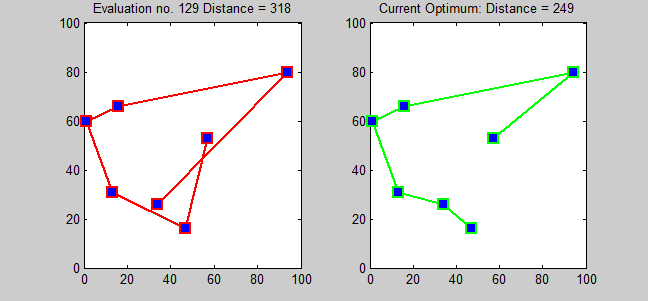 * Progressive improvement algorithms, which use techniques reminiscent of
* Progressive improvement algorithms, which use techniques reminiscent of
 The nearest neighbour (NN) algorithm (a
The nearest neighbour (NN) algorithm (a
 The algorithm of Christofides and Serdyukov follows a similar outline but combines the minimum spanning tree with a solution of another problem, minimum-weight
The algorithm of Christofides and Serdyukov follows a similar outline but combines the minimum spanning tree with a solution of another problem, minimum-weight
 The pairwise exchange or '' 2-opt'' technique involves iteratively removing two edges and replacing them with two different edges that reconnect the fragments created by edge removal into a new and shorter tour. Similarly, the 3-opt technique removes 3 edges and reconnects them to form a shorter tour. These are special cases of the ''k''-opt method. The label ''Lin–Kernighan'' is an often heard misnomer for 2-opt; Lin–Kernighan is actually the more general ''k''-opt method.
For Euclidean instances, 2-opt heuristics give on average solutions that are about 5% better than those yielded by Christofides' algorithm. If we start with an initial solution made with a
The pairwise exchange or '' 2-opt'' technique involves iteratively removing two edges and replacing them with two different edges that reconnect the fragments created by edge removal into a new and shorter tour. Similarly, the 3-opt technique removes 3 edges and reconnects them to form a shorter tour. These are special cases of the ''k''-opt method. The label ''Lin–Kernighan'' is an often heard misnomer for 2-opt; Lin–Kernighan is actually the more general ''k''-opt method.
For Euclidean instances, 2-opt heuristics give on average solutions that are about 5% better than those yielded by Christofides' algorithm. If we start with an initial solution made with a

NP-hard
In computational complexity theory, a computational problem ''H'' is called NP-hard if, for every problem ''L'' which can be solved in non-deterministic polynomial-time, there is a polynomial-time reduction from ''L'' to ''H''. That is, assumi ...
problem in combinatorial optimization
Combinatorial optimization is a subfield of mathematical optimization that consists of finding an optimal object from a finite set of objects, where the set of feasible solutions is discrete or can be reduced to a discrete set. Typical combina ...
, important in theoretical computer science
Theoretical computer science is a subfield of computer science and mathematics that focuses on the Abstraction, abstract and mathematical foundations of computation.
It is difficult to circumscribe the theoretical areas precisely. The Associati ...
and operations research
Operations research () (U.S. Air Force Specialty Code: Operations Analysis), often shortened to the initialism OR, is a branch of applied mathematics that deals with the development and application of analytical methods to improve management and ...
.
The travelling purchaser problem, the vehicle routing problem
The vehicle routing problem (VRP) is a combinatorial optimization and integer programming problem which asks "What is the optimal set of routes for a fleet of vehicles to traverse in order to deliver to a given set of customers?" It generalises ...
and the ring star problem are three generalizations of TSP.
The decision version of the TSP (where given a length ''L'', the task is to decide whether the graph has a tour whose length is at most ''L'') belongs to the class of NP-complete
In computational complexity theory, NP-complete problems are the hardest of the problems to which ''solutions'' can be verified ''quickly''.
Somewhat more precisely, a problem is NP-complete when:
# It is a decision problem, meaning that for any ...
problems. Thus, it is possible that the worst-case running time for any algorithm for the TSP increases superpolynomially (but no more than exponentially) with the number of cities.
The problem was first formulated in 1930 and is one of the most intensively studied problems in optimization. It is used as a benchmark for many optimization methods. Even though the problem is computationally difficult, many heuristic
A heuristic or heuristic technique (''problem solving'', '' mental shortcut'', ''rule of thumb'') is any approach to problem solving that employs a pragmatic method that is not fully optimized, perfected, or rationalized, but is nevertheless ...
s and exact algorithm In computer science and operations research, exact algorithms are algorithms that always solve an optimization problem to optimality.
Unless P = NP, an exact algorithm for an NP-hardness , NP-hard optimization problem cannot run in worst-case poly ...
s are known, so that some instances with tens of thousands of cities can be solved completely, and even problems with millions of cities can be approximated within a small fraction of 1%.
The TSP has several applications even in its purest formulation, such as planning
Planning is the process of thinking regarding the activities required to achieve a desired goal. Planning is based on foresight, the fundamental capacity for mental time travel. Some researchers regard the evolution of forethought - the cap ...
, logistics
Logistics is the part of supply chain management that deals with the efficient forward and reverse flow of goods, services, and related information from the point of origin to the Consumption (economics), point of consumption according to the ...
, and the manufacture of microchips
An integrated circuit (IC), also known as a microchip or simply chip, is a set of electronic circuits, consisting of various electronic components (such as transistors, resistors, and capacitors) and their interconnections. These components a ...
. Slightly modified, it appears as a sub-problem in many areas, such as DNA sequencing
DNA sequencing is the process of determining the nucleic acid sequence – the order of nucleotides in DNA. It includes any method or technology that is used to determine the order of the four bases: adenine, thymine, cytosine, and guanine. The ...
. In these applications, the concept ''city'' represents, for example, customers, soldering points, or DNA fragments, and the concept ''distance'' represents travelling times or cost, or a similarity measure
In statistics and related fields, a similarity measure or similarity function or similarity metric is a real-valued function that quantifies the similarity between two objects. Although no single definition of a similarity exists, usually such mea ...
between DNA fragments. The TSP also appears in astronomy, as astronomers observing many sources want to minimize the time spent moving the telescope between the sources; in such problems, the TSP can be embedded inside an optimal control problem. In many applications, additional constraints such as limited resources or time windows may be imposed.
History
The origins of the travelling salesman problem are unclear. A handbook for travelling salesmen from 1832 mentions the problem and includes example tours throughGermany
Germany, officially the Federal Republic of Germany, is a country in Central Europe. It lies between the Baltic Sea and the North Sea to the north and the Alps to the south. Its sixteen States of Germany, constituent states have a total popu ...
and Switzerland
Switzerland, officially the Swiss Confederation, is a landlocked country located in west-central Europe. It is bordered by Italy to the south, France to the west, Germany to the north, and Austria and Liechtenstein to the east. Switzerland ...
, but contains no mathematical treatment.
 The TSP was mathematically formulated in the 19th century by the Irish mathematician
The TSP was mathematically formulated in the 19th century by the Irish mathematician William Rowan Hamilton
Sir William Rowan Hamilton (4 August 1805 – 2 September 1865) was an Irish astronomer, mathematician, and physicist who made numerous major contributions to abstract algebra, classical mechanics, and optics. His theoretical works and mathema ...
and by the British mathematician Thomas Kirkman
Thomas Penyngton Kirkman FRS (31 March 1806 – 3 February 1895) was a British mathematician and ordained minister of the Church of England. Despite being primarily a churchman, he maintained an active interest in research-level mathematics, a ...
. Hamilton's icosian game
The icosian game is a mathematical game invented in 1856 by Irish mathematician William Rowan Hamilton. It involves finding a Hamiltonian cycle on a dodecahedron, a polygon using edges of the dodecahedron that passes through all its vertex (geo ...
was a recreational puzzle based on finding a Hamiltonian cycle
In the mathematics, mathematical field of graph theory, a Hamiltonian path (or traceable path) is a path (graph theory), path in an undirected or directed graph that visits each vertex (graph theory), vertex exactly once. A Hamiltonian cycle (or ...
. The general form of the TSP appears to have been first studied by mathematicians during the 1930s in Vienna and at Harvard
Harvard University is a private Ivy League research university in Cambridge, Massachusetts, United States. Founded in 1636 and named for its first benefactor, the Puritan clergyman John Harvard, it is the oldest institution of higher lear ...
, notably by Karl Menger
Karl Menger (; January 13, 1902 – October 5, 1985) was an Austrian-born American mathematician, the son of the economist Carl Menger. In mathematics, Menger studied the theory of algebra over a field, algebras and the dimension theory of low-r ...
, who defines the problem, considers the obvious brute-force algorithm, and observes the non-optimality of the nearest neighbour heuristic:
It was first considered mathematically in the 1930s by Merrill M. Flood, who was looking to solve a school bus routing problem. Hassler Whitney
Hassler Whitney (March 23, 1907 – May 10, 1989) was an American mathematician. He was one of the founders of singularity theory, and did foundational work in manifolds, embeddings, immersion (mathematics), immersions, characteristic classes and, ...
at Princeton University
Princeton University is a private university, private Ivy League research university in Princeton, New Jersey, United States. Founded in 1746 in Elizabeth, New Jersey, Elizabeth as the College of New Jersey, Princeton is the List of Colonial ...
generated interest in the problem, which he called the "48 states problem". The earliest publication using the phrase "travelling r travelingsalesman problem" was the 1949 RAND Corporation
The RAND Corporation, doing business as RAND, is an American nonprofit global policy think tank, research institute, and public sector consulting firm. RAND engages in research and development (R&D) in several fields and industries. Since the ...
report by Julia Robinson
Julia Hall Bowman Robinson (December 8, 1919July 30, 1985) was an American mathematician noted for her contributions to the fields of computability theory and computational complexity theory—most notably in decision problems. Her work on Hilber ...
, "On the Hamiltonian game (a traveling salesman problem)."A detailed treatment of the connection between Menger and Whitney as well as the growth in the study of TSP can be found in .
In the 1950s and 1960s, the problem became increasingly popular in scientific circles in Europe and the United States after the RAND Corporation
The RAND Corporation, doing business as RAND, is an American nonprofit global policy think tank, research institute, and public sector consulting firm. RAND engages in research and development (R&D) in several fields and industries. Since the ...
in Santa Monica
Santa Monica (; Spanish language, Spanish: ''Santa Mónica'') is a city in Los Angeles County, California, Los Angeles County, situated along Santa Monica Bay on California's South Coast (California), South Coast. Santa Monica's 2020 United Sta ...
offered prizes for steps in solving the problem. Notable contributions were made by George Dantzig, Delbert Ray Fulkerson, and Selmer M. Johnson from the RAND Corporation, who expressed the problem as an integer linear program and developed the cutting plane method for its solution. They wrote what is considered the seminal paper on the subject in which, with these new methods, they solved an instance with 49 cities to optimality by constructing a tour and proving that no other tour could be shorter. Dantzig, Fulkerson, and Johnson, however, speculated that, given a near-optimal solution, one may be able to find optimality or prove optimality by adding a small number of extra inequalities (cuts). They used this idea to solve their initial 49-city problem using a string model. They found they only needed 26 cuts to come to a solution for their 49 city problem. While this paper did not give an algorithmic approach to TSP problems, the ideas that lay within it were indispensable to later creating exact solution methods for the TSP, though it would take 15 years to find an algorithmic approach in creating these cuts. As well as cutting plane methods, Dantzig, Fulkerson, and Johnson used branch-and-bound
Branch and bound (BB, B&B, or BnB) is a method for solving optimization problems by breaking them down into smaller sub-problems and using a bounding function to eliminate sub-problems that cannot contain the optimal solution.
It is an algorithm ...
algorithms perhaps for the first time.
In 1959, Jillian Beardwood, J.H. Halton, and John Hammersley
John Michael Hammersley, (21 March 1920 – 2 May 2004) was a British mathematician best known for his foundational work in the theory of self-avoiding walks and percolation theory.
Early life and education
Hammersley was born in Helensburgh i ...
published an article entitled "The Shortest Path Through Many Points" in the journal of the Cambridge Philosophical Society
The Cambridge Philosophical Society (CPS) is a scientific society at the University of Cambridge. It was founded in 1819. The name derives from the medieval use of the word philosophy to denote any research undertaken outside the fields of law ...
. The Beardwood–Halton–Hammersley theorem provides a practical solution to the travelling salesman problem. The authors derived an asymptotic formula to determine the length of the shortest route for a salesman who starts at a home or office and visits a fixed number of locations before returning to the start.
In the following decades, the problem was studied by many researchers from mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ...
, computer science
Computer science is the study of computation, information, and automation. Computer science spans Theoretical computer science, theoretical disciplines (such as algorithms, theory of computation, and information theory) to Applied science, ...
, chemistry
Chemistry is the scientific study of the properties and behavior of matter. It is a physical science within the natural sciences that studies the chemical elements that make up matter and chemical compound, compounds made of atoms, molecules a ...
, physics
Physics is the scientific study of matter, its Elementary particle, fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge whi ...
, and other sciences. In the 1960s, however, a new approach was created that, instead of seeking optimal solutions, would produce a solution whose length is provably bounded by a multiple of the optimal length, and in doing so would create lower bounds for the problem; these lower bounds would then be used with branch-and-bound approaches. One method of doing this was to create a minimum spanning tree
A minimum spanning tree (MST) or minimum weight spanning tree is a subset of the edges of a connected, edge-weighted undirected graph that connects all the vertices together, without any cycles and with the minimum possible total edge weight. ...
of the graph and then double all its edges, which produces the bound that the length of an optimal tour is at most twice the weight of a minimum spanning tree.
In 1976, Christofides and Serdyukov (independently of each other) made a big advance in this direction: the Christofides–Serdyukov algorithm yields a solution that, in the worst case, is at most 1.5 times longer than the optimal solution. As the algorithm was simple and quick, many hoped it would give way to a near-optimal solution method. However, this hope for improvement did not immediately materialize, and the Christofides–Serdyukov algorithm remained the method with the best worst-case scenario until 2011, when a (very) slightly improved approximation algorithm was developed for the subset of "graphical" TSPs. In 2020, this tiny improvement was extended to the full (metric) TSP.
Richard M. Karp showed in 1972 that the Hamiltonian cycle
In the mathematics, mathematical field of graph theory, a Hamiltonian path (or traceable path) is a path (graph theory), path in an undirected or directed graph that visits each vertex (graph theory), vertex exactly once. A Hamiltonian cycle (or ...
problem was NP-complete
In computational complexity theory, NP-complete problems are the hardest of the problems to which ''solutions'' can be verified ''quickly''.
Somewhat more precisely, a problem is NP-complete when:
# It is a decision problem, meaning that for any ...
, which implies the NP-hard
In computational complexity theory, a computational problem ''H'' is called NP-hard if, for every problem ''L'' which can be solved in non-deterministic polynomial-time, there is a polynomial-time reduction from ''L'' to ''H''. That is, assumi ...
ness of TSP. This supplied a mathematical explanation for the apparent computational difficulty of finding optimal tours.
Great progress was made in the late 1970s and 1980, when Grötschel, Padberg, Rinaldi and others managed to exactly solve instances with up to 2,392 cities, using cutting planes and branch-and-bound
Branch and bound (BB, B&B, or BnB) is a method for solving optimization problems by breaking them down into smaller sub-problems and using a bounding function to eliminate sub-problems that cannot contain the optimal solution.
It is an algorithm ...
.
In the 1990s, Applegate, Bixby, Chvátal, and Cook
Cook or The Cook may refer to:
Food preparation
* Cooking, the preparation of food
* Cook (domestic worker), a household staff member who prepares food
* Cook (profession), an individual who prepares food for consumption in the food industry
* C ...
developed the program ''Concorde'' that has been used in many recent record solutions. Gerhard Reinelt published the TSPLIB in 1991, a collection of benchmark instances of varying difficulty, which has been used by many research groups for comparing results. In 2006, Cook and others computed an optimal tour through an 85,900-city instance given by a microchip layout problem, currently the largest solved TSPLIB instance. For many other instances with millions of cities, solutions can be found that are guaranteed to be within 2–3% of an optimal tour..
Description
As a graph problem
complete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge. A complete digraph is a directed graph in which every pair of distinct vertices i ...
(i.e., each pair of vertices is connected by an edge). If no path exists between two cities, then adding a sufficiently long edge will complete the graph without affecting the optimal tour.
Asymmetric and symmetric
In the ''symmetric TSP'', the distance between two cities is the same in each opposite direction, forming anundirected graph
In discrete mathematics, particularly in graph theory, a graph is a structure consisting of a set of objects where some pairs of the objects are in some sense "related". The objects are represented by abstractions called '' vertices'' (also call ...
. This symmetry halves the number of possible solutions. In the ''asymmetric TSP'', paths may not exist in both directions or the distances might be different, forming a directed graph. Traffic congestion, one-way streets, and airfares for cities with different departure and arrival fees are real-world considerations that could yield a TSP problem in asymmetric form.
Related problems
* An equivalent formulation in terms ofgraph theory
In mathematics and computer science, graph theory is the study of ''graph (discrete mathematics), graphs'', which are mathematical structures used to model pairwise relations between objects. A graph in this context is made up of ''Vertex (graph ...
is: Given a complete weighted graph (where the vertices would represent the cities, the edges would represent the roads, and the weights would be the cost or distance of that road), find a Hamiltonian cycle
In the mathematics, mathematical field of graph theory, a Hamiltonian path (or traceable path) is a path (graph theory), path in an undirected or directed graph that visits each vertex (graph theory), vertex exactly once. A Hamiltonian cycle (or ...
with the least weight. This is more general than the Hamiltonian path problem
The Hamiltonian path problem is a topic discussed in the fields of complexity theory and graph theory. It decides if a directed or undirected graph, ''G'', contains a Hamiltonian path, a path that visits every vertex in the graph exactly once. T ...
, which only asks if a Hamiltonian path (or cycle) exists in a non-complete unweighted graph.
* The requirement of returning to the starting city does not change the computational complexity
In computer science, the computational complexity or simply complexity of an algorithm is the amount of resources required to run it. Particular focus is given to computation time (generally measured by the number of needed elementary operations ...
of the problem; see Hamiltonian path problem
The Hamiltonian path problem is a topic discussed in the fields of complexity theory and graph theory. It decides if a directed or undirected graph, ''G'', contains a Hamiltonian path, a path that visits every vertex in the graph exactly once. T ...
.
* Another related problem is the bottleneck travelling salesman problem: Find a Hamiltonian cycle in a weighted graph
This is a glossary of graph theory. Graph theory is the study of graphs, systems of nodes or vertices connected in pairs by lines or edges.
Symbols
A
B
...
with the minimal weight of the weightiest edge
Edge or EDGE may refer to:
Technology Computing
* Edge computing, a network load-balancing system
* Edge device, an entry point to a computer network
* Adobe Edge, a graphical development application
* Microsoft Edge, a web browser developed by ...
. A real-world example is avoiding narrow streets with big buses. The problem is of considerable practical importance, apart from evident transportation and logistics areas. A classic example is in printed circuit
A printed circuit board (PCB), also called printed wiring board (PWB), is a laminated sandwich structure of conductive and insulating layers, each with a pattern of traces, planes and other features (similar to wires on a flat surface) ...
manufacturing: scheduling of a route of the drill
A drill is a tool used for making round holes or driving fasteners. It is fitted with a drill bit for making holes, or a screwdriver bit for securing fasteners. Historically, they were powered by hand, and later mains power, but cordless b ...
machine to drill holes in a PCB. In robotic machining or drilling applications, the "cities" are parts to machine or holes (of different sizes) to drill, and the "cost of travel" includes time for retooling the robot (single-machine job sequencing problem).
* The generalized travelling salesman problem, also known as the "travelling politician problem", deals with "states" that have (one or more) "cities", and the salesman must visit exactly one city from each state. One application is encountered in ordering a solution to the cutting stock problem
In operations research, the cutting-stock problem is the problem of cutting standard-sized pieces of Inventory, stock material, such as paper rolls or sheet metal, into pieces of specified sizes while minimizing material wasted. It is an optimizat ...
in order to minimize knife changes. Another is concerned with drilling in semiconductor
A semiconductor is a material with electrical conductivity between that of a conductor and an insulator. Its conductivity can be modified by adding impurities (" doping") to its crystal structure. When two regions with different doping level ...
manufacturing; see e.g., . Noon and Bean demonstrated that the generalized travelling salesman problem can be transformed into a standard TSP with the same number of cities, but a modified distance matrix
In mathematics, computer science and especially graph theory, a distance matrix is a square matrix (two-dimensional array) containing the distances, taken pairwise, between the elements of a set. Depending upon the application involved, the ''dist ...
.
* The sequential ordering problem deals with the problem of visiting a set of cities, where precedence relations between the cities exist.
* A common interview question at Google
Google LLC (, ) is an American multinational corporation and technology company focusing on online advertising, search engine technology, cloud computing, computer software, quantum computing, e-commerce, consumer electronics, and artificial ...
is how to route data among data processing nodes; routes vary by time to transfer the data, but nodes also differ by their computing power and storage, compounding the problem of where to send data.
* The travelling purchaser problem deals with a purchaser who is charged with purchasing a set of products. He can purchase these products in several cities, but at different prices, and not all cities offer the same products. The objective is to find a route between a subset of the cities that minimizes total cost (travel cost + purchasing cost) and enables the purchase of all required products.
Integer linear programming formulations
The TSP can be formulated as an integer linear program. Several formulations are known. Two notable formulations are the Miller–Tucker–Zemlin (MTZ) formulation and the Dantzig–Fulkerson–Johnson (DFJ) formulation. The DFJ formulation is stronger, though the MTZ formulation is still useful in certain settings. Common to both these formulations is that one labels the cities with the numbers and takes to be the cost (distance) from city to city . The main variables in the formulations are: : It is because these are 0/1 variables that the formulations become integer programs; all other constraints are purely linear. In particular, the objective in the program is to minimize the tour length : Without further constraints, the will effectively range over all subsets of the set of edges, which is very far from the sets of edges in a tour, and allows for a trivial minimum where all . Therefore, both formulations also have the constraints that, at each vertex, there is exactly one incoming edge and one outgoing edge, which may be expressed as the linear equations : for and for These ensure that the chosen set of edges locally looks like that of a tour, but still allow for solutions violating the global requirement that there is ''one'' tour which visits all vertices, as the edges chosen could make up several tours, each visiting only a subset of the vertices; arguably, it is this global requirement that makes TSP a hard problem. The MTZ and DFJ formulations differ in how they express this final requirement as linear constraints.Miller–Tucker–Zemlin formulation
In addition to the variables as above, there is for each a dummy variable that keeps track of the order in which the cities are visited, counting from city the interpretation is that implies city is visited before city For a given tour (as encoded into values of the variables), one may find satisfying values for the variables by making equal to the number of edges along that tour, when going from city to city Because linear programming favors non-strict inequalities () over strict we would like to impose constraints to the effect that : if Merely requiring would ''not'' achieve that, because this also requires when which is not correct. Instead MTZ use the linear constraints : for all distinct where the constant term provides sufficient slack that does not impose a relation between and The way that the variables then enforce that a single tour visits all cities is that they increase by at least for each step along a tour, with a decrease only allowed where the tour passes through city That constraint would be violated by every tour which does not pass through city so the only way to satisfy it is that the tour passing city also passes through all other cities. The MTZ formulation of TSP is thus the following integer linear programming problem: : The first set of equalities requires that each city is arrived at from exactly one other city, and the second set of equalities requires that from each city there is a departure to exactly one other city. The last constraint enforces that there is only a single tour covering all cities, and not two or more disjointed tours that only collectively cover all cities.Dantzig–Fulkerson–Johnson formulation
Label the cities with the numbers 1, ..., ''n'' and define: : Take to be the distance from city ''i'' to city ''j''. Then TSP can be written as the following integer linear programming problem: : The last constraint of the DFJ formulation—called a ''subtour elimination'' constraint—ensures that no proper subset Q can form a sub-tour, so the solution returned is a single tour and not the union of smaller tours. Intuitively, for each proper subset Q of the cities, the constraint requires that there be fewer edges than cities in Q: if there were to be as many edges in Q as cities in Q, that would represent a subtour of the cities of Q. Because this leads to an exponential number of possible constraints, in practice it is solved with row generation.Computing a solution
The traditional lines of attack for the NP-hard problems are the following: * Devisingexact algorithm In computer science and operations research, exact algorithms are algorithms that always solve an optimization problem to optimality.
Unless P = NP, an exact algorithm for an NP-hardness , NP-hard optimization problem cannot run in worst-case poly ...
s, which work reasonably fast only for small problem sizes.
* Devising "suboptimal" or heuristic algorithm
A heuristic or heuristic technique (''problem solving'', '' mental shortcut'', ''rule of thumb'') is any approach to problem solving that employs a pragmatic method that is not fully optimized, perfected, or rationalized, but is nevertheless ...
s, i.e., algorithms that deliver approximated solutions in a reasonable time.
* Finding special cases for the problem ("subproblems") for which either better or exact heuristics are possible.
Exact algorithms
The most direct solution would be to try allpermutation
In mathematics, a permutation of a set can mean one of two different things:
* an arrangement of its members in a sequence or linear order, or
* the act or process of changing the linear order of an ordered set.
An example of the first mean ...
s (ordered combinations) and see which one is cheapest (using brute-force search
In computer science, brute-force search or exhaustive search, also known as generate and test, is a very general problem-solving technique and algorithmic paradigm that consists of Iteration#Computing, systematically checking all possible candida ...
). The running time for this approach lies within a polynomial factor of , the factorial
In mathematics, the factorial of a non-negative denoted is the Product (mathematics), product of all positive integers less than or equal The factorial also equals the product of n with the next smaller factorial:
\begin
n! &= n \times ...
of the number of cities, so this solution becomes impractical even for only 20 cities.
One of the earliest applications of dynamic programming is the Held–Karp algorithm, which solves the problem in time . This bound has also been reached by Exclusion-Inclusion in an attempt preceding the dynamic programming approach.
 Improving these time bounds seems to be difficult. For example, it has not been determined whether a classical
Improving these time bounds seems to be difficult. For example, it has not been determined whether a classical exact algorithm In computer science and operations research, exact algorithms are algorithms that always solve an optimization problem to optimality.
Unless P = NP, an exact algorithm for an NP-hardness , NP-hard optimization problem cannot run in worst-case poly ...
for TSP that runs in time exists. The currently best quantum exact algorithm In computer science and operations research, exact algorithms are algorithms that always solve an optimization problem to optimality.
Unless P = NP, an exact algorithm for an NP-hardness , NP-hard optimization problem cannot run in worst-case poly ...
for TSP due to Ambainis et al. runs in time .
Other approaches include:
* Various branch-and-bound
Branch and bound (BB, B&B, or BnB) is a method for solving optimization problems by breaking them down into smaller sub-problems and using a bounding function to eliminate sub-problems that cannot contain the optimal solution.
It is an algorithm ...
algorithms, which can be used to process TSPs containing thousands of cities.
 * Progressive improvement algorithms, which use techniques reminiscent of
* Progressive improvement algorithms, which use techniques reminiscent of linear programming
Linear programming (LP), also called linear optimization, is a method to achieve the best outcome (such as maximum profit or lowest cost) in a mathematical model whose requirements and objective are represented by linear function#As a polynomia ...
. This works well for up to 200 cities.
* Implementations of branch-and-bound
Branch and bound (BB, B&B, or BnB) is a method for solving optimization problems by breaking them down into smaller sub-problems and using a bounding function to eliminate sub-problems that cannot contain the optimal solution.
It is an algorithm ...
and problem-specific cut generation ( branch-and-cut); this is the method of choice for solving large instances. This approach holds the current record, solving an instance with 85,900 cities, see .
An exact solution for 15,112 German towns from TSPLIB was found in 2001 using the cutting-plane method
In mathematical optimization, the cutting-plane method is any of a variety of optimization methods that iteratively refine a feasible set or objective function by means of linear inequalities, termed ''cuts''. Such procedures are commonly used ...
proposed by George Dantzig, Ray Fulkerson, and Selmer M. Johnson in 1954, based on linear programming
Linear programming (LP), also called linear optimization, is a method to achieve the best outcome (such as maximum profit or lowest cost) in a mathematical model whose requirements and objective are represented by linear function#As a polynomia ...
. The computations were performed on a network of 110 processors located at Rice University
William Marsh Rice University, commonly referred to as Rice University, is a Private university, private research university in Houston, Houston, Texas, United States. Established in 1912, the university spans 300 acres.
Rice University comp ...
and Princeton University
Princeton University is a private university, private Ivy League research university in Princeton, New Jersey, United States. Founded in 1746 in Elizabeth, New Jersey, Elizabeth as the College of New Jersey, Princeton is the List of Colonial ...
. The total computation time was equivalent to 22.6 years on a single 500 MHz Alpha processor. In May 2004, the travelling salesman problem of visiting all 24,978 towns in Sweden was solved: a tour of length approximately 72,500 kilometres was found, and it was proven that no shorter tour exists. In March 2005, the travelling salesman problem of visiting all 33,810 points in a circuit board was solved using '' Concorde TSP Solver'': a tour of length 66,048,945 units was found, and it was proven that no shorter tour exists. The computation took approximately 15.7 CPU-years (Cook et al. 2006). In April 2006 an instance with 85,900 points was solved using ''Concorde TSP Solver'', taking over 136 CPU-years; see .
Heuristic and approximation algorithms
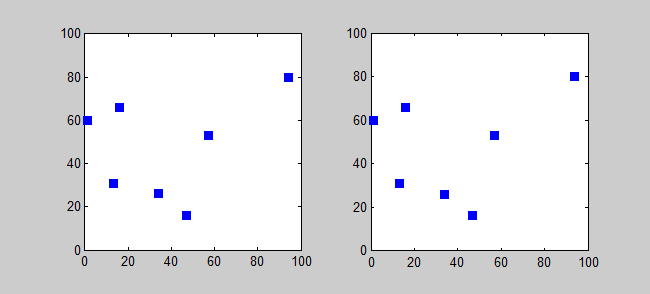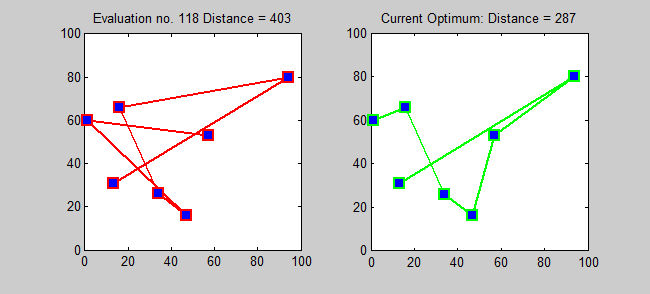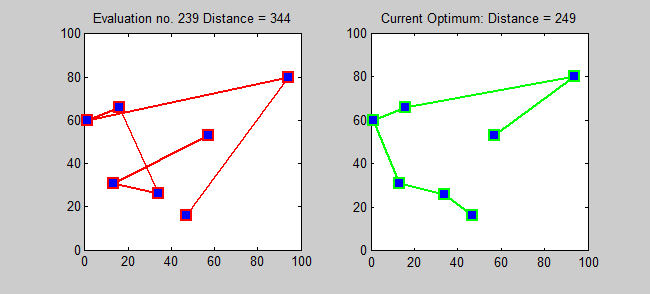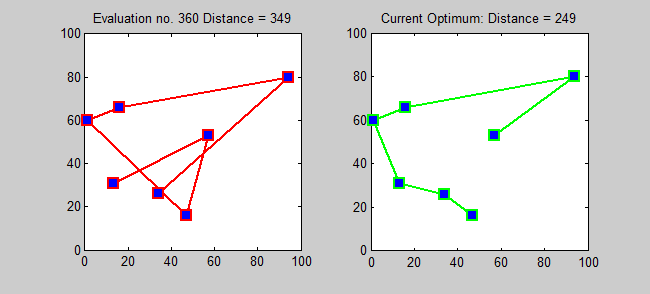
Variousheuristics
A heuristic or heuristic technique (''problem solving'', '' mental shortcut'', ''rule of thumb'') is any approach to problem solving that employs a pragmatic method that is not fully optimized, perfected, or rationalized, but is nevertheless ...
and approximation algorithm
In computer science and operations research, approximation algorithms are efficient algorithms that find approximate solutions to optimization problems (in particular NP-hard problems) with provable guarantees on the distance of the returned sol ...
s, which quickly yield good solutions, have been devised. These include the multi-fragment algorithm. Modern methods can find solutions for extremely large problems (millions of cities) within a reasonable time which are, with a high probability, just 2–3% away from the optimal solution.
Several categories of heuristics are recognized.
Constructive heuristics
 The nearest neighbour (NN) algorithm (a
The nearest neighbour (NN) algorithm (a greedy algorithm
A greedy algorithm is any algorithm that follows the problem-solving heuristic of making the locally optimal choice at each stage. In many problems, a greedy strategy does not produce an optimal solution, but a greedy heuristic can yield locally ...
) lets the salesman choose the nearest unvisited city as his next move. This algorithm quickly yields an effectively short route. For ''N'' cities randomly distributed on a plane, the algorithm on average yields a path 25% longer than the shortest possible path; however, there exist many specially-arranged city distributions which make the NN algorithm give the worst route. This is true for both asymmetric and symmetric TSPs. Rosenkrantz et al. showed that the NN algorithm has the approximation factor for instances satisfying the triangle inequality. A variation of the NN algorithm, called nearest fragment (NF) operator, which connects a group (fragment) of nearest unvisited cities, can find shorter routes with successive iterations. The NF operator can also be applied on an initial solution obtained by the NN algorithm for further improvement in an elitist model, where only better solutions are accepted.
The bitonic tour
In computational geometry, a bitonic tour of a set of point sites in the Euclidean plane is a closed polygonal chain that has each site as one of its vertices, such that any vertical line crosses the chain at most twice.
Optimal bitonic tours
...
of a set of points is the minimum-perimeter monotone polygon
In geometry, a polygon in the plane is called monotone with respect to a straight line , if every line orthogonal to intersects the boundary of at most twice.
Similarly, a polygonal chain is called monotone with respect to a straight line ...
that has the points as its vertices; it can be computed efficiently with dynamic programming.
Another constructive heuristic, Match Twice and Stitch (MTS), performs two sequential matchings, where the second matching is executed after deleting all the edges of the first matching, to yield a set of cycles. The cycles are then stitched to produce the final tour.
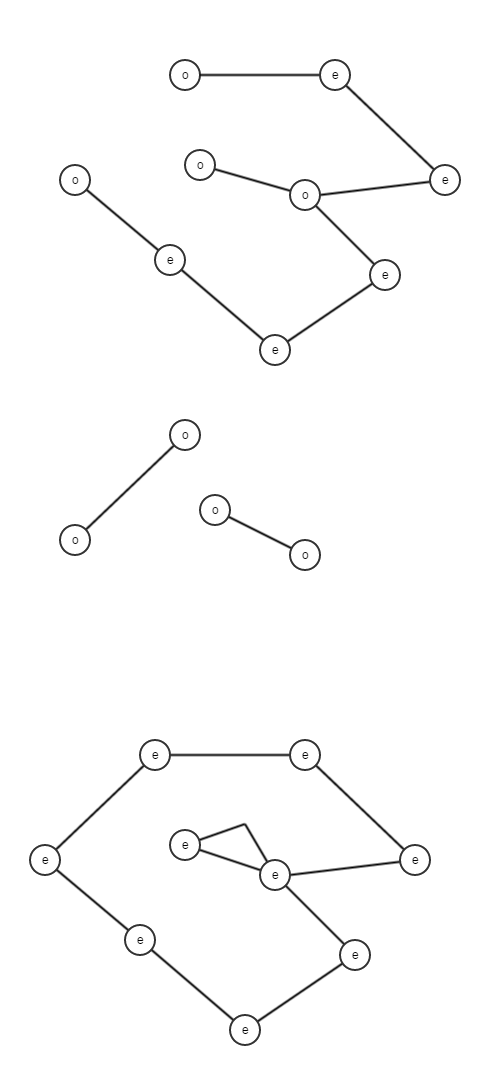
The Algorithm of Christofides and Serdyukov

 The algorithm of Christofides and Serdyukov follows a similar outline but combines the minimum spanning tree with a solution of another problem, minimum-weight
The algorithm of Christofides and Serdyukov follows a similar outline but combines the minimum spanning tree with a solution of another problem, minimum-weight perfect matching
In graph theory, a perfect matching in a graph is a matching that covers every vertex of the graph. More formally, given a graph with edges and vertices , a perfect matching in is a subset of , such that every vertex in is adjacent to exact ...
. This gives a TSP tour which is at most 1.5 times the optimal. It was one of the first approximation algorithm
In computer science and operations research, approximation algorithms are efficient algorithms that find approximate solutions to optimization problems (in particular NP-hard problems) with provable guarantees on the distance of the returned sol ...
s, and was in part responsible for drawing attention to approximation algorithms as a practical approach to intractable problems. As a matter of fact, the term "algorithm" was not commonly extended to approximation algorithms until later; the Christofides algorithm was initially referred to as the Christofides heuristic.
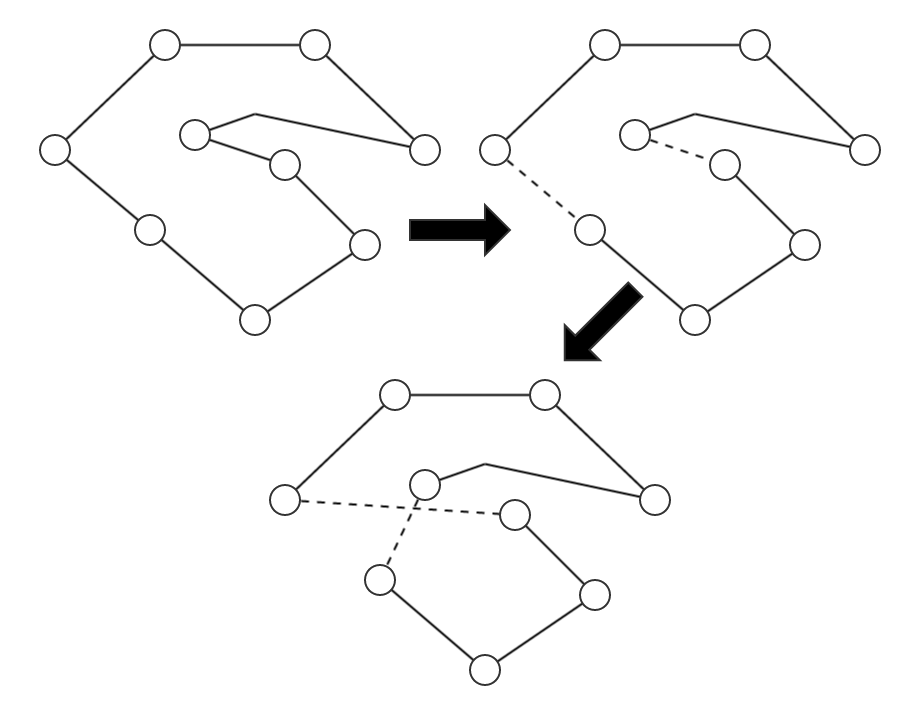
This algorithm looks at things differently by using a result from graph theory which helps improve on the lower bound of the TSP which originated from doubling the cost of the minimum spanning tree. Given an Eulerian graph, we can find an Eulerian tour in time, so if we had an Eulerian graph with cities from a TSP as vertices, then we can easily see that we could use such a method for finding an Eulerian tour to find a TSP solution. By the triangle inequality
In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side.
This statement permits the inclusion of Degeneracy (mathematics)#T ...
, we know that the TSP tour can be no longer than the Eulerian tour, and we therefore have a lower bound for the TSP. Such a method is described below.
# Find a minimum spanning tree for the problem.
# Create duplicates for every edge to create an Eulerian graph.
# Find an Eulerian tour for this graph.
# Convert to TSP: if a city is visited twice, then create a shortcut from the city before this in the tour to the one after this.
To improve the lower bound, a better way of creating an Eulerian graph is needed. By the triangle inequality, the best Eulerian graph must have the same cost as the best travelling salesman tour; hence, finding optimal Eulerian graphs is at least as hard as TSP. One way of doing this is by minimum weight matching using algorithms with a complexity of .
Making a graph into an Eulerian graph starts with the minimum spanning tree; all the vertices of odd order must then be made even, so a matching for the odd-degree vertices must be added, which increases the order of every odd-degree vertex by 1. This leaves us with a graph where every vertex is of even order, which is thus Eulerian. Adapting the above method gives the algorithm of Christofides and Serdyukov:
# Find a minimum spanning tree for the problem.
# Create a matching for the problem with the set of cities of odd order.
# Find an Eulerian tour for this graph.
# Convert to TSP using shortcuts.
Pairwise exchange
 The pairwise exchange or '' 2-opt'' technique involves iteratively removing two edges and replacing them with two different edges that reconnect the fragments created by edge removal into a new and shorter tour. Similarly, the 3-opt technique removes 3 edges and reconnects them to form a shorter tour. These are special cases of the ''k''-opt method. The label ''Lin–Kernighan'' is an often heard misnomer for 2-opt; Lin–Kernighan is actually the more general ''k''-opt method.
For Euclidean instances, 2-opt heuristics give on average solutions that are about 5% better than those yielded by Christofides' algorithm. If we start with an initial solution made with a
The pairwise exchange or '' 2-opt'' technique involves iteratively removing two edges and replacing them with two different edges that reconnect the fragments created by edge removal into a new and shorter tour. Similarly, the 3-opt technique removes 3 edges and reconnects them to form a shorter tour. These are special cases of the ''k''-opt method. The label ''Lin–Kernighan'' is an often heard misnomer for 2-opt; Lin–Kernighan is actually the more general ''k''-opt method.
For Euclidean instances, 2-opt heuristics give on average solutions that are about 5% better than those yielded by Christofides' algorithm. If we start with an initial solution made with a greedy algorithm
A greedy algorithm is any algorithm that follows the problem-solving heuristic of making the locally optimal choice at each stage. In many problems, a greedy strategy does not produce an optimal solution, but a greedy heuristic can yield locally ...
, then the average number of moves greatly decreases again and is ; however, for random starts, the average number of moves is . While this is a small increase in size, the initial number of moves for small problems is 10 times as big for a random start compared to one made from a greedy heuristic. This is because such 2-opt heuristics exploit 'bad' parts of a solution such as crossings. These types of heuristics are often used within vehicle routing problem
The vehicle routing problem (VRP) is a combinatorial optimization and integer programming problem which asks "What is the optimal set of routes for a fleet of vehicles to traverse in order to deliver to a given set of customers?" It generalises ...
heuristics to re-optimize route solutions.
''k''-opt heuristic, or Lin–Kernighan heuristics
The Lin–Kernighan heuristic is a special case of the ''V''-opt or variable-opt technique. It involves the following steps: # Given a tour, delete ''k'' mutually disjoint edges. # Reassemble the remaining fragments into a tour, leaving no disjoint subtours (that is, do not connect a fragment's endpoints together). This in effect simplifies the TSP under consideration into a much simpler problem. # Each fragment endpoint can be connected to other possibilities: of 2''k'' total fragment endpoints available, the two endpoints of the fragment under consideration are disallowed. Such a constrained 2''k''-city TSP can then be solved with brute-force methods to find the least-cost recombination of the original fragments. The most popular of the ''k''-opt methods are 3-opt, as introduced by Shen Lin ofBell Labs
Nokia Bell Labs, commonly referred to as ''Bell Labs'', is an American industrial research and development company owned by Finnish technology company Nokia. With headquarters located in Murray Hill, New Jersey, Murray Hill, New Jersey, the compa ...
in 1965. A special case of 3-opt is where the edges are not disjoint (two of the edges are adjacent to one another). In practice, it is often possible to achieve substantial improvement over 2-opt without the combinatorial cost of the general 3-opt by restricting the 3-changes to this special subset where two of the removed edges are adjacent. This so-called two-and-a-half-opt typically falls roughly midway between 2-opt and 3-opt, both in terms of the quality of tours achieved and the time required to achieve those tours.
''V''-opt heuristic
The variable-opt method is related to, and a generalization of, the ''k''-opt method. Whereas the ''k''-opt methods remove a fixed number (''k'') of edges from the original tour, the variable-opt methods do not fix the size of the edge set to remove. Instead, they grow the set as the search process continues. The best-known method in this family is the Lin–Kernighan method (mentioned above as a misnomer for 2-opt). Shen Lin andBrian Kernighan
Brian Wilson Kernighan (; born January 30, 1942) is a Canadian computer scientist.
He worked at Bell Labs and contributed to the development of Unix alongside Unix creators Ken Thompson and Dennis Ritchie. Kernighan's name became widely known ...
first published their method in 1972, and it was the most reliable heuristic for solving travelling salesman problems for nearly two decades. More advanced variable-opt methods were developed at Bell Labs in the late 1980s by David Johnson and his research team. These methods (sometimes called Lin–Kernighan–Johnson) build on the Lin–Kernighan method, adding ideas from tabu search Tabu search (TS) is a metaheuristic search method employing local search methods used for mathematical optimization. It was created by Fred W. Glover in 1986
and formalized in 1989.
Local (neighborhood) searches take a potential solution to a ...
and evolutionary computing. The basic Lin–Kernighan technique gives results that are guaranteed to be at least 3-opt. The Lin–Kernighan–Johnson methods compute a Lin–Kernighan tour, and then perturb the tour by what has been described as a mutation that removes at least four edges and reconnects the tour in a different way, then ''V''-opting the new tour. The mutation is often enough to move the tour from the local minimum
In mathematical analysis, the maximum and minimum of a function are, respectively, the greatest and least value taken by the function. Known generically as extremum, they may be defined either within a given range (the ''local'' or ''relative ...
identified by Lin–Kernighan. ''V''-opt methods are widely considered the most powerful heuristics for the problem, and are able to address special cases, such as the Hamilton Cycle Problem and other non-metric TSPs that other heuristics fail on. For many years, Lin–Kernighan–Johnson had identified optimal solutions for all TSPs where an optimal solution was known and had identified the best-known solutions for all other TSPs on which the method had been tried.
Randomized improvement
OptimizedMarkov chain
In probability theory and statistics, a Markov chain or Markov process is a stochastic process describing a sequence of possible events in which the probability of each event depends only on the state attained in the previous event. Informally ...
algorithms which use local searching heuristic sub-algorithms can find a route extremely close to the optimal route for 700 to 800 cities.
TSP is a touchstone for many general heuristics devised for combinatorial optimization such as genetic algorithm
In computer science and operations research, a genetic algorithm (GA) is a metaheuristic inspired by the process of natural selection that belongs to the larger class of evolutionary algorithms (EA). Genetic algorithms are commonly used to g ...
s, simulated annealing
Simulated annealing (SA) is a probabilistic technique for approximating the global optimum of a given function. Specifically, it is a metaheuristic to approximate global optimization in a large search space for an optimization problem. ...
, tabu search Tabu search (TS) is a metaheuristic search method employing local search methods used for mathematical optimization. It was created by Fred W. Glover in 1986
and formalized in 1989.
Local (neighborhood) searches take a potential solution to a ...
, ant colony optimization
In computer science and operations research, the ant colony optimization algorithm (ACO) is a probabilistic technique for solving computational problems that can be reduced to finding good paths through graphs. Artificial ants represent multi ...
, river formation dynamics (see swarm intelligence
Swarm intelligence (SI) is the collective behavior of decentralized, self-organized systems, natural or artificial. The concept is employed in work on artificial intelligence. The expression was introduced by Gerardo Beni and Jing Wang in 198 ...
), and the cross entropy method.
Constricting Insertion Heuristic
This starts with a sub-tour such as theconvex hull
In geometry, the convex hull, convex envelope or convex closure of a shape is the smallest convex set that contains it. The convex hull may be defined either as the intersection of all convex sets containing a given subset of a Euclidean space, ...
and then inserts other vertices.
Ant colony optimization
Artificial intelligence
Artificial intelligence (AI) is the capability of computer, computational systems to perform tasks typically associated with human intelligence, such as learning, reasoning, problem-solving, perception, and decision-making. It is a field of re ...
researcher Marco Dorigo described in 1993 a method of heuristically generating "good solutions" to the TSP using a simulation of an ant colony called ''ACS'' (''ant colony system''). It models behavior observed in real ants to find short paths between food sources and their nest, an emergent behavior resulting from each ant's preference to follow trail pheromones deposited by other ants.
ACS sends out a large number of virtual ant agents to explore many possible routes on the map. Each ant probabilistically chooses the next city to visit based on a heuristic combining the distance to the city and the amount of virtual pheromone deposited on the edge to the city. The ants explore, depositing pheromone on each edge that they cross, until they have all completed a tour. At this point the ant which completed the shortest tour deposits virtual pheromone along its complete tour route (''global trail updating''). The amount of pheromone deposited is inversely proportional to the tour length: the shorter the tour, the more it deposits.
Special cases
Metric
In the ''metric TSP'', also known as ''delta-TSP'' or Δ-TSP, the intercity distances satisfy thetriangle inequality
In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side.
This statement permits the inclusion of Degeneracy (mathematics)#T ...
.
A very natural restriction of the TSP is to require that the distances between cities form a metric
Metric or metrical may refer to:
Measuring
* Metric system, an internationally adopted decimal system of measurement
* An adjective indicating relation to measurement in general, or a noun describing a specific type of measurement
Mathematics
...
to satisfy the triangle inequality
In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side.
This statement permits the inclusion of Degeneracy (mathematics)#T ...
; that is, the direct connection from ''A'' to ''B'' is never farther than the route via intermediate ''C'':
:.
The edges then build a metric
Metric or metrical may refer to:
Measuring
* Metric system, an internationally adopted decimal system of measurement
* An adjective indicating relation to measurement in general, or a noun describing a specific type of measurement
Mathematics
...
on the set of vertices. When the cities are viewed as points in the plane, many natural distance function
In mathematics, a metric space is a set together with a notion of ''distance'' between its elements, usually called points. The distance is measured by a function called a metric or distance function. Metric spaces are a general setting fo ...
s are metrics, and so many natural instances of TSP satisfy this constraint.
The following are some examples of metric TSPs for various metrics.
*In the Euclidean TSP (see below), the distance between two cities is the Euclidean distance
In mathematics, the Euclidean distance between two points in Euclidean space is the length of the line segment between them. It can be calculated from the Cartesian coordinates of the points using the Pythagorean theorem, and therefore is o ...
between the corresponding points.
*In the rectilinear TSP, the distance between two cities is the sum of the absolute values of the differences of their ''x''- and ''y''-coordinates. This metric is often called the Manhattan distance
Taxicab geometry or Manhattan geometry is geometry where the familiar Euclidean distance is ignored, and the distance between two point (geometry), points is instead defined to be the sum of the absolute differences of their respective Cartesian ...
or city-block metric.
*In the maximum metric, the distance between two points is the maximum of the absolute values of differences of their ''x''- and ''y''-coordinates.
The last two metrics appear, for example, in routing a machine that drills a given set of holes in a printed circuit board
A printed circuit board (PCB), also called printed wiring board (PWB), is a Lamination, laminated sandwich structure of electrical conduction, conductive and Insulator (electricity), insulating layers, each with a pattern of traces, planes ...
. The Manhattan metric corresponds to a machine that adjusts first one coordinate, and then the other, so the time to move to a new point is the sum of both movements. The maximum metric corresponds to a machine that adjusts both coordinates simultaneously, so the time to move to a new point is the slower of the two movements.
In its definition, the TSP does not allow cities to be visited twice, but many applications do not need this constraint. In such cases, a symmetric, non-metric instance can be reduced to a metric one. This replaces the original graph with a complete graph in which the inter-city distance is replaced by the shortest path
In graph theory, the shortest path problem is the problem of finding a path between two vertices (or nodes) in a graph such that the sum of the weights of its constituent edges is minimized.
The problem of finding the shortest path between two ...
length between ''A'' and ''B'' in the original graph.
Euclidean
For points in theEuclidean plane
In mathematics, a Euclidean plane is a Euclidean space of Two-dimensional space, dimension two, denoted \textbf^2 or \mathbb^2. It is a geometric space in which two real numbers are required to determine the position (geometry), position of eac ...
, the optimal solution to the travelling salesman problem forms a simple polygon
In geometry, a simple polygon is a polygon that does not Intersection (Euclidean geometry), intersect itself and has no holes. That is, it is a Piecewise linear curve, piecewise-linear Jordan curve consisting of finitely many line segments. The ...
through all of the points, a polygonalization of the points. Any non-optimal solution with crossings can be made into a shorter solution without crossings by local optimizations. The Euclidean distance
In mathematics, the Euclidean distance between two points in Euclidean space is the length of the line segment between them. It can be calculated from the Cartesian coordinates of the points using the Pythagorean theorem, and therefore is o ...
obeys the triangle inequality, so the Euclidean TSP forms a special case of metric TSP. However, even when the input points have integer coordinates, their distances generally take the form of square root
In mathematics, a square root of a number is a number such that y^2 = x; in other words, a number whose ''square'' (the result of multiplying the number by itself, or y \cdot y) is . For example, 4 and −4 are square roots of 16 because 4 ...
s, and the length of a tour is a sum of radicals In mathematics, a sum of radicals is defined as a finite linear combination of th roots:
:\sum_^n k_i\sqrt _i
where n, r_i are natural numbers and k_i, x_i are real numbers.
A particular special case arising in computational complexity theory is ...
, making it difficult to perform the symbolic computation
In mathematics and computer science, computer algebra, also called symbolic computation or algebraic computation, is a scientific area that refers to the study and development of algorithms and software for manipulating mathematical expressions ...
needed to perform exact comparisons of the lengths of different tours.
Like the general TSP, the exact Euclidean TSP is NP-hard, but the issue with sums of radicals is an obstacle to proving that its decision version is in NP, and therefore NP-complete. A discretized version of the problem with distances rounded to integers is NP-complete. With rational coordinates and the actual Euclidean metric, Euclidean TSP is known to be in the Counting Hierarchy, a subclass of PSPACE. With arbitrary real coordinates, Euclidean TSP cannot be in such classes, since there are uncountably many possible inputs. Despite these complications, Euclidean TSP is much easier than the general metric case for approximation. For example, the minimum spanning tree of the graph associated with an instance of the Euclidean TSP is a Euclidean minimum spanning tree, and so can be computed in expected ''O''(''n'' log ''n'') time for ''n'' points (considerably less than the number of edges). This enables the simple 2-approximation algorithm for TSP with triangle inequality above to operate more quickly.
In general, for any ''c'' > 0, where ''d'' is the number of dimensions in the Euclidean space, there is a polynomial-time algorithm that finds a tour of length at most (1 + 1/''c'') times the optimal for geometric instances of TSP in
:
time; this is called a polynomial-time approximation scheme
In computer science (particularly algorithmics), a polynomial-time approximation scheme (PTAS) is a type of approximation algorithm for optimization problems (most often, NP-hard optimization problems).
A PTAS is an algorithm which takes an inst ...
(PTAS). Sanjeev Arora and Joseph S. B. Mitchell were awarded the Gödel Prize
The Gödel Prize is an annual prize for outstanding papers in the area of theoretical computer science, given jointly by the European Association for Theoretical Computer Science (EATCS) and the Association for Computing Machinery Special Inter ...
in 2010 for their concurrent discovery of a PTAS for the Euclidean TSP.
In practice, simpler heuristics with weaker guarantees continue to be used.
Asymmetric
In most cases, the distance between two nodes in the TSP network is the same in both directions. The case where the distance from ''A'' to ''B'' is not equal to the distance from ''B'' to ''A'' is called asymmetric TSP. A practical application of an asymmetric TSP is route optimization using street-level routing (which is made asymmetric by one-way streets, slip-roads, motorways, etc.). The stacker crane problem can be viewed as a special case of the asymmetric TSP. In this problem, the input consists of ordered pairs of points in a metric space, which must be visited consecutively in order by the tour. These pairs of points can be viewed as the nodes of an asymmetric TSP, with asymmetric distances reflecting the combined cost of traveling from the first point of a pair to its second and then from the second point of a pair to the first point of the next pair.Conversion to symmetric
Solving an asymmetric TSP graph can be somewhat complex. The following is a 3×3 matrix containing all possible path weights between the nodes ''A'', ''B'' and ''C''. One option is to turn an asymmetric matrix of size ''N'' into a symmetric matrix of size 2''N''. : To double the size, each of the nodes in the graph is duplicated, creating a second ''ghost node'', linked to the original node with a "ghost" edge of very low (possibly negative) weight, here denoted −''w''. (Alternatively, the ghost edges have weight 0, and weight w is added to all other edges.) The original 3×3 matrix shown above is visible in the bottom left and the transpose of the original in the top-right. Both copies of the matrix have had their diagonals replaced by the low-cost hop paths, represented by −''w''. In the new graph, no edge directly links original nodes and no edge directly links ghost nodes. : The weight −''w'' of the "ghost" edges linking the ghost nodes to the corresponding original nodes must be low enough to ensure that all ghost edges must belong to any optimal symmetric TSP solution on the new graph (''w'' = 0 is not always low enough). As a consequence, in the optimal symmetric tour, each original node appears next to its ghost node (e.g. a possible path is ), and by merging the original and ghost nodes again we get an (optimal) solution of the original asymmetric problem (in our example, ).Analyst's problem
There is an analogous problem ingeometric measure theory
In mathematics, geometric measure theory (GMT) is the study of geometric properties of sets (typically in Euclidean space) through measure theory. It allows mathematicians to extend tools from differential geometry to a much larger class of surfac ...
which asks the following: under what conditions may a subset ''E'' of Euclidean space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are ''Euclidean spaces ...
be contained in a rectifiable curve
Arc length is the distance between two points along a section of a curve. Development of a formulation of arc length suitable for applications to mathematics and the sciences is a problem in vector calculus and in differential geometry. In the ...
(that is, when is there a curve with finite length that visits every point in ''E'')? This problem is known as the analyst's travelling salesman problem.
Path length for random sets of points in a square
Suppose are independent random variables with uniform distribution in the square , and let be the shortest path length (i.e. TSP solution) for this set of points, according to the usualEuclidean distance
In mathematics, the Euclidean distance between two points in Euclidean space is the length of the line segment between them. It can be calculated from the Cartesian coordinates of the points using the Pythagorean theorem, and therefore is o ...
. It is known that, almost surely,
::
where is a positive constant that is not known explicitly. Since (see below), it follows from bounded convergence theorem that , hence lower and upper bounds on follow from bounds on