Eisenstein Integer

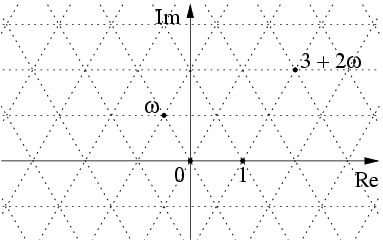In mathematics, the Eisenstein integers (named after Gotthold Eisenstein), occasionally also known as Eulerian integers (after Leonhard Euler), are the complex numbers of the form
: $z = a + b\omega ,$
where and are integers and
: $\omega = \frac = e^$
is a primitive (hence non-real) cube root of unity.

The Eisenstein integers form a triangular lattice in the complex plane, in contrast with the Gaussian integers, which form a square lattice in the complex plane. The Eisenstein integers are a countably infinite set.

Properties

The Eisenstein integers form a commutative ring of algebraic integers in the algebraic number field – the third cyclotomic field. To see that the Eisenstein integers are algebraic integers note that each is a root of the monic polynomial
: $z^2 - (2a - b)\;\!z + \left(a^2 - ab + b^2\right)~.$
In particular, satisfies the equation
: $\omega^2 + \omega + 1 = 0~.$

The product of two Eisenstein integers and is given explicitly by
: $(a + b\;\!\omega) \;\! (c + d\;\!\omega)=(ac - bd) + (bc + ad - bd)\;\!\omega~.$

The 2-norm of an Eisenstein integer is just its squared modulus, and is given by
: $^2 \,= \, ^2 + \tfrac b^2 \, = \, a^2 - ab + b^2~,$
which is clearly a positive ordinary (rational) integer.

Also, the complex conjugate of satisfies
: $\bar\omega = \omega^2~.$

The group of units in this ring is the cyclic group formed by the sixth roots of unity in the complex plane: , the Eisenstein integers of norm .

Euclidean domain

The ring of Eisenstein integers forms a Euclidean domain whose norm is given by the square modulus, as above:
: $N(a+b\,\omega) = a^2 - a b + b^2.$

A division algorithm, applied to any dividend and divisor , gives a quotient and a remainder smaller than the divisor, satisfying:
: $\alpha = \kappa \beta +\rho \ \ \text\ \ N(\rho) < N(\beta).$

Here, , , , are all Eisenstein integers. This algorithm implies the Euclidean algorithm, which proves Euclid's lemma and the unique factorization of Eisenstein integers into Eisenstein primes.

One division algorithm is as follows. First perform the division in the field of complex numbers, and write the quotient in terms of :
: $\frac\ =\ \tfrac\alpha\overline \ =\ a+bi \ =\ a+\tfracb+\tfracb\omega,$
for rational . Then obtain the Eisenstein integer quotient by rounding the rational coefficients to the nearest integer:
: $\kappa = \left\lfloor a+\tfracb\right\rceil + \left\lfloor \tfracb\right\rceil\omega \ \ \text\ \ \rho = - \kappa\beta.$
Here $\lfloor x\rceil$ may denote any of the standard rounding-to-integer functions.

The reason this satisfies , while the analogous procedure fails for most other quadratic integer rings, is as follows. A fundamental domain for the ideal , acting by translations on the complex plane, is the 60°–120° rhombus with vertices , , , . Any Eisenstein integer lies inside one of the translates of this parallelogram, and the quotient is one of its vertices. The remainder is the square distance from to this vertex, but the maximum possible distance in our algorithm is only $\tfrac2 , \beta,$, so $, \rho, \leq \tfrac2 , \beta, < , \beta,$. (The size of could be slightly decreased by taking to be the closest corner.)

Eisenstein primes

If and are Eisenstein integers, we say that divides if there is some Eisenstein integer such that . A non-unit Eisenstein integer is said to be an Eisenstein prime if its only non-unit divisors are of the form , where is any of the six units. They are the corresponding concept to the Gaussian primes in the Gaussian integers.

There are two types of Eisenstein prime.
* an ordinary prime number (or ''rational prime'') which is congruent to is also an Eisenstein prime.
* and each rational prime congruent to are equal to the norm of an Eisenstein integer . Thus, such a prime may be factored as , and these factors are Eisenstein primes: they are precisely the Eisenstein integers whose norm is a rational prime.

In the second type, factors of , $1-\omega$ and $1-\omega^2$ are associates: $1-\omega=(-\omega)(1-\omega^2)$, so it is regarded as a special type in some books.

The first few Eisenstein primes of the form are:
: 2, 5, 11, 17, 23, 29, 41, 47, 53, 59, 71, 83, 89, 101, ... .

Natural primes that are congruent to or modulo are ''not'' Eisenstein primes: they admit nontrivial factorizations in . For example:
:
: .

In general, if a natural prime is modulo and can therefore be written as , then it factorizes over as
: .

Some non-real Eisenstein primes are
: , , , , , , .

Up to conjugacy and unit multiples, the primes listed above, together with and , are all the Eisenstein primes of absolute value not exceeding .

, the largest known real Eisenstein prime is the tenth-largest known prime , discovered by Péter Szabolcs and PrimeGrid. With one exception, all larger known primes are Mersenne primes, discovered by GIMPS. Real Eisenstein primes are congruent to , and all Mersenne primes greater than are congruent to ; thus no Mersenne prime is an Eisenstein prime.

Eisenstein series

The sum of the reciprocals of all Eisenstein integers excluding raised to the fourth power is :
$\sum_\frac=G_4\left(e^\right)=0$
so $e^$ is a root of j-invariant.
In general $G_k\left(e^\right)=0$ if and only if $k\not\equiv 0 \pmod 6$.

The sum of the reciprocals of all Eisenstein integers excluding raised to the sixth power can be expressed in terms of the gamma function:
$\sum_\frac=G_6\left(e^\right)=\frac$
where are the Eisenstein integers and is the Eisenstein series of weight 6.

Quotient of by the Eisenstein integers

The quotient of the complex plane by the lattice containing all Eisenstein integers is a complex torus of real dimension . This is one of two tori with maximal symmetry among all such complex tori. This torus can be obtained by identifying each of the three pairs of opposite edges of a regular hexagon.

The other maximally symmetric torus is the quotient of the complex plane by the additive lattice of Gaussian integers, and can be obtained by identifying each of the two pairs of opposite sides of a square fundamental domain, such as .

See also

* Gaussian integer
* Cyclotomic field
* Systolic geometry
* Hermite constant
* Cubic reciprocity
* Loewner's torus inequality
* Hurwitz quaternion
* Quadratic integer
* Dixon elliptic functions
* Equianharmonic

Notes

External links

Eisenstein Integer--from MathWorld

{{Systolic geometry navbox

Algebraic numbers
Quadratic irrational numbers
Cyclotomic fields
Lattice points
Systolic geometry
Integers