|
Gotthold Eisenstein
Ferdinand Gotthold Max Eisenstein (16 April 1823 – 11 October 1852) was a German mathematician who made significant contributions to number theory and mathematical analysis, analysis. Born in Berlin, Prussia, to Jewish parents who converted to Protestantism before his birth, Eisenstein displayed exceptional mathematical talent from a young age. Early life and education Despite suffering from health problems, including meningitis, Eisenstein excelled academically. At 14, he attended Friedrich Werder Gymnasium (school), Gymnasium. By age 15, he had mastered the mathematics curriculum. His teachers recognized his mathematical abilities, one quoted as saying: He then turned to the works of Leonhard Euler and Joseph-Louis Lagrange to study differential calculus. While still a student, Eisenstein began attending lectures by Peter Gustav Lejeune Dirichlet and others at the University of Berlin. In 1843, he met William Rowan Hamilton in Dublin, who introduced him to Niels Henrik A ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kingdom Of Prussia
The Kingdom of Prussia (, ) was a German state that existed from 1701 to 1918.Marriott, J. A. R., and Charles Grant Robertson. ''The Evolution of Prussia, the Making of an Empire''. Rev. ed. Oxford: Clarendon Press, 1946. It played a significant role in the unification of Germany in 1871 and was a major constituent of the German Empire until its German Revolution of 1918–1919, dissolution in 1918. Although it took its name from the Prussia (region), region called Prussia, it was based in the Margraviate of Brandenburg. Its capital was Berlin. The list of monarchs of Prussia, kings of Prussia were from the House of Hohenzollern. The polity of Brandenburg-Prussia, predecessor of the kingdom, became a military power under Frederick William, Elector of Brandenburg, known as "The Great Elector". As a kingdom, Prussia continued its rise to power, especially during the reign of Frederick the Great, Frederick II "the Great".Horn, D. B. "The Youth of Frederick the Great 1712–30." ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quartic Reciprocity
Quartic or biquadratic reciprocity is a collection of theorems in elementary and algebraic number theory that state conditions under which the congruence ''x''4 ≡ ''p'' (mod ''q'') is solvable; the word "reciprocity" comes from the form of some of these theorems, in that they relate the solvability of the congruence ''x''4 ≡ ''p'' (mod ''q'') to that of ''x''4 ≡ ''q'' (mod ''p''). History Euler made the first conjectures about biquadratic reciprocity. Gauss published two monographs on biquadratic reciprocity. In the first one (1828) he proved Euler's conjecture about the biquadratic character of 2. In the second one (1832) he stated the biquadratic reciprocity law for the Gaussian integers and proved the supplementary formulas. He saidGauss, BQ, § 67 that a third monograph would be forthcoming with the proof of the general theorem, but it never appeared. Jacobi presented proofs in his Königsberg lectures of 1836–37. The first published proofs were by Ei ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
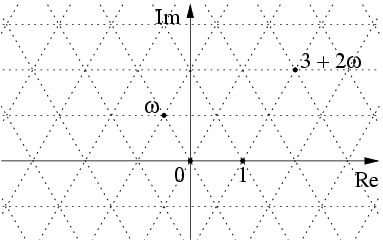
Eisenstein Prime
In mathematics, the Eisenstein integers (named after Gotthold Eisenstein), occasionally also known as Eulerian integers (after Leonhard Euler), are the complex numbers of the form : z = a + b\omega , where and are integers and : \omega = \frac = e^ is a primitive (hence non-real) cube root of unity. The Eisenstein integers form a triangular lattice in the complex plane, in contrast with the Gaussian integers, which form a square lattice in the complex plane. The Eisenstein integers are a countably infinite set. Properties The Eisenstein integers form a commutative ring of algebraic integers in the algebraic number field – the third cyclotomic field. To see that the Eisenstein integers are algebraic integers note that each is a root of the monic polynomial : z^2 - (2a - b)\;\!z + \left(a^2 - ab + b^2\right)~. In particular, satisfies the equation : \omega^2 + \omega + 1 = 0~. The product of two Eisenstein integers and is given explicitly by : (a + b\;\!\omega) \;\ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eisenstein Ideal
In mathematics, the Eisenstein ideal is an ideal in the endomorphism ring of the Jacobian variety of a modular curve, consisting roughly of elements of the Hecke algebra of Hecke operators that annihilate the Eisenstein series. It was introduced by , in studying the rational points of modular curves. An Eisenstein prime is a prime in the support of the Eisenstein ideal (this has nothing to do with primes in the Eisenstein integers). Definition Let ''N'' be a rational prime, and define :''J''0(''N'') = ''J'' as the Jacobian variety of the modular curve :''X''0(''N'') = ''X''. There are endomorphisms ''T''''l'' of ''J'' for each prime number ''l'' not dividing ''N''. These come from the Hecke operator, considered first as an algebraic correspondence on ''X'', and from there as acting on divisor classes, which gives the action on ''J''. There is also a Fricke involution ''w'' (and Atkin–Lehner involutions if ''N'' is composite). The Eisenstein ideal, in the (unital) subring ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eisenstein's Criterion
In mathematics, Eisenstein's criterion gives a sufficient condition for a polynomial with integer coefficients to be irreducible over the rational numbers – that is, for it to not be factorizable into the product of non-constant polynomials with rational coefficients. This criterion is not applicable to all polynomials with integer coefficients that are irreducible over the rational numbers, but it does allow in certain important cases for irreducibility to be proved with very little effort. It may apply either directly or after transformation of the original polynomial. This criterion is named after Gotthold Eisenstein. In the early 20th century, it was also known as the Schönemann–Eisenstein theorem because Theodor Schönemann was the first to publish it. Criterion Suppose we have the following polynomial with integer coefficients: Q(x) = a_n x^n + a_ x^ + \cdots + a_1 x + a_0. If there exists a prime number such that the following three conditions all apply: * divid ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tuberculosis
Tuberculosis (TB), also known colloquially as the "white death", or historically as consumption, is a contagious disease usually caused by ''Mycobacterium tuberculosis'' (MTB) bacteria. Tuberculosis generally affects the lungs, but it can also affect other parts of the body. Most infections show no symptoms, in which case it is known as inactive or latent tuberculosis. A small proportion of latent infections progress to active disease that, if left untreated, can be fatal. Typical symptoms of active TB are chronic cough with hemoptysis, blood-containing sputum, mucus, fever, night sweats, and weight loss. Infection of other organs can cause a wide range of symptoms. Tuberculosis is Human-to-human transmission, spread from one person to the next Airborne disease, through the air when people who have active TB in their lungs cough, spit, speak, or sneeze. People with latent TB do not spread the disease. A latent infection is more likely to become active in those with weakened I ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
German Academy Of Sciences At Berlin
The German Academy of Sciences at Berlin, , in 1972 renamed the Academy of Sciences of the GDR (''Akademie der Wissenschaften der DDR (AdW)''), was the most eminent Research institute, research institution of East Germany (German Democratic Republic, GDR). The academy was established in 1946 in an attempt to continue the tradition of the Prussian Academy of Sciences and the Brandenburg Society of Sciences, founded in 1700 by Gottfried Wilhelm Leibniz. The academy was a learned society (scholarship society), in which awarded membership via election constituted scientific recognition. Unlike other academies of science, the DAW was also the host organization of a scientific community of non-academic research institutes. Upon German reunification, the Academy's learned society was dissociated from its research institutes and any other affiliates and eventually dissolved in 1992. Since 1993, activities of the AdW's members and college have been continued by the newly established Leib ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Göttingen Academy Of Sciences And Humanities
The Göttingen Academy of Sciences (name since 2023 : )Note that the German ''Wissenschaft'' has a wider meaning than the English "Science", and includes Social sciences and Humanities. is the oldest continuously existing institution among the eight scientific academies in Germany, which are united under the umbrella of the Union of German Academies of Sciences and Humanities. It has the task of promoting research under its own auspices and in collaboration with academics in and outside Germany. It has its seat in the university town of Göttingen. Its meeting room is located in the auditorium of the University of Göttingen. History The ''Königliche Gesellschaft der Wissenschaften'' (''Royal Society of Sciences'') was founded in 1751 by King George II of Great Britain, who was also Prince-Elector of the Holy Roman Empire and Duke of Brunswick-Lüneburg (House of Hanover), the German state in which Göttingen was located. The first president was the Swiss natural historian and p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reciprocity Law
In mathematics, a reciprocity law is a generalization of the law of quadratic reciprocity to arbitrary monic irreducible polynomials f(x) with integer coefficients. Recall that first reciprocity law, quadratic reciprocity, determines when an irreducible polynomial f(x) = x^2 + ax + b splits into linear terms when reduced mod p. That is, it determines for which prime numbers the relationf(x) \equiv f_p(x) = (x-n_p)(x-m_p) \text (\text p)holds. For a general reciprocity lawpg 3, it is defined as the rule determining which primes p the polynomial f_p splits into linear factors, denoted \text\. There are several different ways to express reciprocity laws. The early reciprocity laws found in the 19th century were usually expressed in terms of a power residue symbol (''p''/''q'') generalizing the quadratic reciprocity symbol, that describes when a prime number is an ''n''th power residue modulo another prime, and gave a relation between (''p''/''q'') and (''q''/''p''). Hilbert ref ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prime Number
A prime number (or a prime) is a natural number greater than 1 that is not a Product (mathematics), product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways of writing it as a product, or , involve 5 itself. However, 4 is composite because it is a product (2 × 2) in which both numbers are smaller than 4. Primes are central in number theory because of the fundamental theorem of arithmetic: every natural number greater than 1 is either a prime itself or can be factorization, factorized as a product of primes that is unique up to their order. The property of being prime is called primality. A simple but slow primality test, method of checking the primality of a given number , called trial division, tests whether is a multiple of any integer between 2 and . Faster algorithms include the Miller–Rabin primality test, which is fast but has a small chance of error ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
University Of Breslau
A university () is an educational institution, institution of tertiary education and research which awards academic degrees in several Discipline (academia), academic disciplines. ''University'' is derived from the Latin phrase , which roughly means "community of teachers and scholars". Universities typically offer both undergraduate education, undergraduate and postgraduate education, postgraduate programs. The first universities in Europe were established by Catholic Church, Catholic monks. The University of Bologna (), Italy, which was founded in 1088, is the first university in the sense of: *being a high degree-awarding institute. *using the word (which was coined at its foundation). *having independence from the ecclesiastic schools and issuing secular as well as non-secular degrees (with teaching conducted by both clergy and non-clergy): grammar, rhetoric, logic, theology, canon law and notarial law.Hunt Janin: "The university in medieval life, 1179–1499", McFarland, 2 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |