|
Hermite Constant
In mathematics, the Hermite constant, named after Charles Hermite, determines how long a shortest element of a lattice in Euclidean space can be. The constant ''γn'' for integers ''n'' > 0 is defined as follows. For a lattice ''L'' in Euclidean space R''n'' with unit covolume, i.e. vol(R''n''/''L'') = 1, let ''λ''1(''L'') denote the least length of a nonzero element of ''L''. Then is the maximum of ''λ''1(''L'') over all such lattices ''L''. The square root in the definition of the Hermite constant is a matter of historical convention. Alternatively, the Hermite constant ''γn'' can be defined as the square of the maximal systole of a flat ''n''-dimensional torus of unit volume. Example The Hermite constant is known in dimensions 1–8 and 24. For ''n'' = 2, one has ''γ''2 = . This value is attained by the hexagonal lattice of the Eisenstein integers, scaled to have a fundamental parallelogram with unit area. The constants for the missing values are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
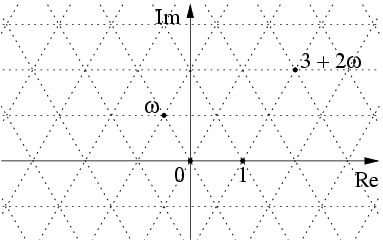
Eisenstein Integers
In mathematics, the Eisenstein integers (named after Gotthold Eisenstein), occasionally also known as Eulerian integers (after Leonhard Euler), are the complex numbers of the form : z = a + b\omega , where and are integers and : \omega = \frac = e^ is a primitive (hence non-real) cube root of unity. The Eisenstein integers form a triangular lattice in the complex plane, in contrast with the Gaussian integers, which form a square lattice in the complex plane. The Eisenstein integers are a countably infinite set. Properties The Eisenstein integers form a commutative ring of algebraic integers in the algebraic number field – the third cyclotomic field. To see that the Eisenstein integers are algebraic integers note that each is a root of the monic polynomial : z^2 - (2a - b)\;\!z + \left(a^2 - ab + b^2\right)~. In particular, satisfies the equation : \omega^2 + \omega + 1 = 0~. The product of two Eisenstein integers and is given explicitly by : (a + b\;\!\omega) \; ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Systolic Geometry
In mathematics, systolic geometry is the study of systolic invariants of manifolds and polyhedra, as initially conceived by Charles Loewner and developed by Mikhail Gromov, Michael Freedman, Peter Sarnak, Mikhail Katz, Larry Guth, and others, in its arithmetical, ergodic, and topological manifestations. See also Introduction to systolic geometry. The notion of systole The ''systole'' of a compact metric space ''X'' is a metric invariant of ''X'', defined to be the least length of a noncontractible loop in ''X'' (i.e. a loop that cannot be contracted to a point in the ambient space ''X''). In more technical language, we minimize length over free loops representing nontrivial conjugacy classes in the fundamental group of ''X''. When ''X'' is a graph, the invariant is usually referred to as the girth, ever since the 1947 article on girth by W. T. Tutte. Possibly inspired by Tutte's article, Loewner started thinking about systolic questions on surfaces in the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Springer-Verlag
Springer Science+Business Media, commonly known as Springer, is a German multinational publishing company of books, e-books and peer-reviewed journals in science, humanities, technical and medical (STM) publishing. Originally founded in 1842 in Berlin, it expanded internationally in the 1960s, and through mergers in the 1990s and a sale to venture capitalists it fused with Wolters Kluwer and eventually became part of Springer Nature in 2015. Springer has major offices in Berlin, Heidelberg, Dordrecht, and New York City. History Julius Springer founded Springer-Verlag in Berlin in 1842 and his son Ferdinand Springer grew it from a small firm of 4 employees into Germany's then second-largest academic publisher with 65 staff in 1872.Chronology ". Springer Science+Business Media. In 1964, Springer expanded its business internationally, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Loewner's Torus Inequality
In differential geometry, Loewner's torus inequality is an inequality due to Charles Loewner. It relates the systole and the area of an arbitrary Riemannian metric on the 2-torus. Statement In 1949 Charles Loewner proved that every metric on the 2-torus \mathbb T^2 satisfies the optimal inequality : \operatorname^2 \leq \frac \operatorname(\mathbb T^2), where "sys" is its systole, i.e. least length of a noncontractible loop. The constant appearing on the right hand side is the Hermite constant \gamma_2 in dimension 2, so that Loewner's torus inequality can be rewritten as : \operatorname^2 \leq \gamma_2\;\operatorname(\mathbb T^2). The inequality was first mentioned in the literature in . Case of equality The boundary case of equality is attained if and only if the metric is flat and homothetic to the so-called ''equilateral torus'', i.e. torus whose group of deck transformations is precisely the hexagonal lattice spanned by the cube roots of unity in \mathbb C. Geometric ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gamma Function
In mathematics, the gamma function (represented by Γ, capital Greek alphabet, Greek letter gamma) is the most common extension of the factorial function to complex numbers. Derived by Daniel Bernoulli, the gamma function \Gamma(z) is defined for all complex numbers z except non-positive integers, and for every positive integer z=n, \Gamma(n) = (n-1)!\,.The gamma function can be defined via a convergent improper integral for complex numbers with positive real part: \Gamma(z) = \int_0^\infty t^ e^\textt, \ \qquad \Re(z) > 0\,.The gamma function then is defined in the complex plane as the analytic continuation of this integral function: it is a meromorphic function which is holomorphic function, holomorphic except at zero and the negative integers, where it has simple Zeros and poles, poles. The gamma function has no zeros, so the reciprocal gamma function is an entire function. In fact, the gamma function corresponds to the Mellin transform of the negative exponential functi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hans Frederick Blichfeldt
Hans Frederick Blichfeldt (1873–1945) was a Danish-American mathematician at Stanford University, known for his contributions to group theory, the representation theory of finite groups, the geometry of numbers, sphere packing, and quadratic forms. He is the namesake of Blichfeldt's theorem. Life Blichfeldt was one of five children of a Danish farming couple, Erhard Christoffer Laurentius Blichfeldt and Nielsine Maria Schlaper; many of his father's ancestors were ministers. He was born on January 9, 1873, in Iller, a village in the Sønderborg Municipality of Denmark. In 1881, the family moved to Copenhagen. In 1888, he passed with high honors the entrance examinations for the University of Copenhagen, but his family was unable to afford sending him to the university. Instead, later the same year, they moved again to the US. He worked for several years as a lumberman, a railway worker, a traveling surveyor, and then as a government draftsman in Bellingham, Washington. In 1894 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fundamental Pair Of Periods
In mathematics, a fundamental pair of periods is an ordered pair of complex numbers that defines a lattice in the complex plane. This type of lattice is the underlying object with which elliptic functions and modular forms are defined. Definition A fundamental pair of periods is a pair of complex numbers \omega_1,\omega_2 \in \Complex such that their ratio \omega_2 / \omega_1 is not real. If considered as vectors in \R^2, the two are linearly independent. The lattice generated by \omega_1 and \omega_2 is :\Lambda = \left\. This lattice is also sometimes denoted as \Lambda(\omega_1, \omega_2) to make clear that it depends on \omega_1 and \omega_2. It is also sometimes denoted by \Omega\vphantom or \Omega(\omega_1, \omega_2), or simply by (\omega_1, \omega_2). The two generators \omega_1 and \omega_2 are called the ''lattice basis''. The parallelogram with vertices (0, \omega_1, \omega_1+\omega_2, \omega_2) is called the ''fundamental parallelogram''. While a fundamental pair gen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hexagonal Lattice
The hexagonal lattice (sometimes called triangular lattice) is one of the five two-dimensional Bravais lattice types. The symmetry category of the lattice is wallpaper group p6m. The primitive translation vectors of the hexagonal lattice form an angle of 120° and are of equal lengths, : , \mathbf a_1, = , \mathbf a_2, = a. The reciprocal lattice of the hexagonal lattice is a hexagonal lattice in reciprocal space with orientation changed by 90° and primitive lattice vectors of length : g=\frac. Honeycomb point set The honeycomb point set is a special case of the hexagonal lattice with a two-atom basis. The centers of the hexagons of a honeycomb form a hexagonal lattice, and the honeycomb point set can be seen as the union of two offset hexagonal lattices. In nature, carbon atoms of the two-dimensional material graphene are arranged in a honeycomb point set. Crystal classes The ''hexagonal lattice'' class names, Schönflies notation, Hermann-Mauguin notation, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Charles Hermite
Charles Hermite () FRS FRSE MIAS (24 December 1822 – 14 January 1901) was a French mathematician who did research concerning number theory, quadratic forms, invariant theory, orthogonal polynomials, elliptic functions, and algebra. Hermite polynomials, Hermite interpolation, Hermite normal form, Hermitian operators, and cubic Hermite splines are named in his honor. One of his students was Henri Poincaré. He was the first to prove that '' e'', the base of natural logarithms, is a transcendental number. His methods were used later by Ferdinand von Lindemann to prove that is transcendental. Life Hermite was born in Dieuze, Moselle, on 24 December 1822, with a deformity in his right foot that would impair his gait throughout his life. He was the sixth of seven children of Ferdinand Hermite and his wife, Madeleine née Lallemand. Ferdinand worked in the drapery business of Madeleine's family while also pursuing a career as an artist. The drapery business relocated to Nan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hexagonal Lattice
The hexagonal lattice (sometimes called triangular lattice) is one of the five two-dimensional Bravais lattice types. The symmetry category of the lattice is wallpaper group p6m. The primitive translation vectors of the hexagonal lattice form an angle of 120° and are of equal lengths, : , \mathbf a_1, = , \mathbf a_2, = a. The reciprocal lattice of the hexagonal lattice is a hexagonal lattice in reciprocal space with orientation changed by 90° and primitive lattice vectors of length : g=\frac. Honeycomb point set The honeycomb point set is a special case of the hexagonal lattice with a two-atom basis. The centers of the hexagons of a honeycomb form a hexagonal lattice, and the honeycomb point set can be seen as the union of two offset hexagonal lattices. In nature, carbon atoms of the two-dimensional material graphene are arranged in a honeycomb point set. Crystal classes The ''hexagonal lattice'' class names, Schönflies notation, Hermann-Mauguin notation, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Torus
In geometry, a torus (: tori or toruses) is a surface of revolution generated by revolving a circle in three-dimensional space one full revolution about an axis that is coplanarity, coplanar with the circle. The main types of toruses include ring toruses, horn toruses, and spindle toruses. A ring torus is sometimes colloquially referred to as a donut or doughnut. If the axis of revolution does not touch the circle, the surface has a ring shape and is called a torus of revolution, also known as a ring torus. If the axis of revolution is tangent to the circle, the surface is a horn torus. If the axis of revolution passes twice through the circle, the surface is a Lemon (geometry), spindle torus (or ''self-crossing torus'' or ''self-intersecting torus''). If the axis of revolution passes through the center of the circle, the surface is a degenerate torus, a double-covered sphere. If the revolved curve is not a circle, the surface is called a ''toroid'', as in a square toroid. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |