Cube (arithmetic) on:
[Wikipedia]
[Google]
[Amazon]
In
 Proofs.
gives a particularly simple derivation, by expanding each cube in the sum into a set of consecutive odd numbers. He begins by giving the identity
:
That identity is related to triangular numbers in the following way:
:
and thus the summands forming start off just after those forming all previous values up to .
Applying this property, along with another well-known identity:
:
we obtain the following derivation:
:
Proofs.
gives a particularly simple derivation, by expanding each cube in the sum into a set of consecutive odd numbers. He begins by giving the identity
:
That identity is related to triangular numbers in the following way:
:
and thus the summands forming start off just after those forming all previous values up to .
Applying this property, along with another well-known identity:
:
we obtain the following derivation:
:
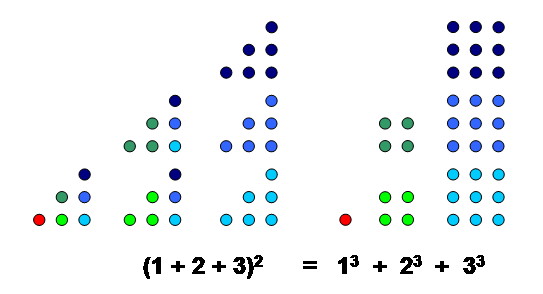 In the more recent mathematical literature, uses the rectangle-counting interpretation of these numbers to form a geometric proof of the identity (see also ); he observes that it may also be proved easily (but uninformatively) by induction, and states that provides "an interesting old Arabic proof". provides a purely visual proof, provide two additional proofs, and gives seven geometric proofs.
For example, the sum of the first 5 cubes is the square of the 5th triangular number,
:
A similar result can be given for the sum of the first odd cubes,
:
but , must satisfy the negative Pell equation . For example, for and , then,
:
:
and so on. Also, every even
In the more recent mathematical literature, uses the rectangle-counting interpretation of these numbers to form a geometric proof of the identity (see also ); he observes that it may also be proved easily (but uninformatively) by induction, and states that provides "an interesting old Arabic proof". provides a purely visual proof, provide two additional proofs, and gives seven geometric proofs.
For example, the sum of the first 5 cubes is the square of the 5th triangular number,
:
A similar result can be given for the sum of the first odd cubes,
:
but , must satisfy the negative Pell equation . For example, for and , then,
:
:
and so on. Also, every even
 There are examples of cubes of numbers in
There are examples of cubes of numbers in
arithmetic
Arithmetic is an elementary branch of mathematics that deals with numerical operations like addition, subtraction, multiplication, and division. In a wider sense, it also includes exponentiation, extraction of roots, and taking logarithms.
...
and algebra
Algebra is a branch of mathematics that deals with abstract systems, known as algebraic structures, and the manipulation of expressions within those systems. It is a generalization of arithmetic that introduces variables and algebraic ope ...
, the cube of a number is its third power, that is, the result of multiplying three instances of together.
The cube of a number is denoted , using a superscript
A subscript or superscript is a character (such as a number or letter) that is set slightly below or above the normal line of type, respectively. It is usually smaller than the rest of the text. Subscripts appear at or below the baseline, wh ...
3, for example . The cube operation can also be defined for any other mathematical expression
In mathematics, an expression is a written arrangement of symbols following the context-dependent, syntactic conventions of mathematical notation. Symbols can denote numbers, variables, operations, and functions. Other symbols include punct ...
, for example .
The cube is also the number multiplied by its square
In geometry, a square is a regular polygon, regular quadrilateral. It has four straight sides of equal length and four equal angles. Squares are special cases of rectangles, which have four equal angles, and of rhombuses, which have four equal si ...
:
:.
The ''cube function'' is the function (often denoted ) that maps a number to its cube. It is an odd function, as
:.
The volume
Volume is a measure of regions in three-dimensional space. It is often quantified numerically using SI derived units (such as the cubic metre and litre) or by various imperial or US customary units (such as the gallon, quart, cubic inch) ...
of a geometric cube is the cube of its side length, giving rise to the name. The inverse operation that consists of finding a number whose cube is is called extracting the cube root
In mathematics, a cube root of a number is a number that has the given number as its third power; that is y^3=x. The number of cube roots of a number depends on the number system that is considered.
Every real number has exactly one real cub ...
of . It determines the side of the cube of a given volume. It is also raised to the one-third power.
The graph of the cube function is known as the cubic parabola. Because the cube function is an odd function, this curve has a center of symmetry at the origin, but no axis of symmetry.
In integers
A cube number, or a perfect cube, or sometimes just a cube, is a number which is the cube of aninteger
An integer is the number zero (0), a positive natural number (1, 2, 3, ...), or the negation of a positive natural number (−1, −2, −3, ...). The negations or additive inverses of the positive natural numbers are referred to as negative in ...
.
The non-negative perfect cubes up to 603 are :
Geometrically speaking, a positive integer is a perfect cube if and only if
In logic and related fields such as mathematics and philosophy, "if and only if" (often shortened as "iff") is paraphrased by the biconditional, a logical connective between statements. The biconditional is true in two cases, where either bo ...
one can arrange solid unit cubes into a larger, solid cube. For example, 27 small cubes can be arranged into one larger one with the appearance of a Rubik's Cube, since .
The difference between the cubes of consecutive integers can be expressed as follows:
:.
or
:.
There is no minimum perfect cube, since the cube of a negative integer is negative. For example, .
Base ten
Unlike perfect squares, perfect cubes do not have a small number of possibilities for the last two digits. Except for cubes divisible by 5, where only 25, 75 and 00 can be the last two digits, ''any'' pair of digits with the last digit odd can occur as the last digits of a perfect cube. With even cubes, there is considerable restriction, for only 00, 2, 4, 6 and 8 can be the last two digits of a perfect cube (where stands for any odd digit and for any even digit). Some cube numbers are also square numbers; for example, 64 is a square number and a cube number . This happens if and only if the number is a perfect sixth power (in this case 2). The last digits of each 3rd power are: It is, however, easy to show that most numbers are not perfect cubes because ''all'' perfect cubes must have digital root 1, 8 or 9. That is their valuesmodulo
In computing and mathematics, the modulo operation returns the remainder or signed remainder of a division, after one number is divided by another, the latter being called the '' modulus'' of the operation.
Given two positive numbers and , mo ...
9 may be only 0, 1, and 8. Moreover, the digital root of any number's cube can be determined by the remainder the number gives when divided by 3:
* If the number ''x'' is divisible by 3, its cube has digital root 9; that is,
*:
* If it has a remainder of 1 when divided by 3, its cube has digital root 1; that is,
*:
* If it has a remainder of 2 when divided by 3, its cube has digital root 8; that is,
*:
Sums of two cubes
Sums of three cubes
It is conjectured that every integer (positive or negative) not congruent to modulo can be written as a sum of three (positive or negative) cubes with infinitely many ways. For example, . Integers congruent to modulo are excluded because they cannot be written as the sum of three cubes. The smallest such integer for which such a sum is not known is 114. In September 2019, the previous smallest such integer with no known 3-cube sum, 42, was found to satisfy this equation: : One solution to is given in the table below for , and not congruent to or modulo . The selected solution is the one that is primitive (), is not of the form or (since they are infinite families of solutions), satisfies , and has minimal values for and (tested in this order). Only primitive solutions are selected since the non-primitive ones can be trivially deduced from solutions for a smaller value of . For example, for , the solution results from the solution by multiplying everything by Therefore, this is another solution that is selected. Similarly, for , the solution is excluded, and this is the solution that is selected.Fermat's Last Theorem for cubes
The equation has no non-trivial (i.e. ) solutions in integers. In fact, it has none in Eisenstein integers. Both of these statements are also true for the equation .Sum of first ''n'' cubes
The sum of the first cubes is the th triangle number squared: :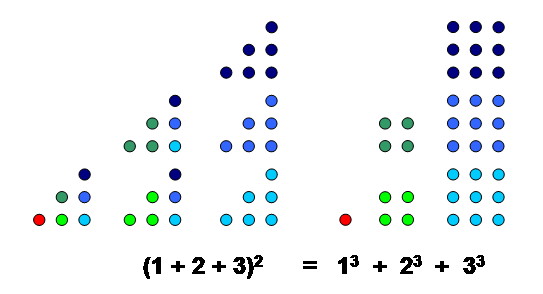 In the more recent mathematical literature, uses the rectangle-counting interpretation of these numbers to form a geometric proof of the identity (see also ); he observes that it may also be proved easily (but uninformatively) by induction, and states that provides "an interesting old Arabic proof". provides a purely visual proof, provide two additional proofs, and gives seven geometric proofs.
For example, the sum of the first 5 cubes is the square of the 5th triangular number,
:
A similar result can be given for the sum of the first odd cubes,
:
but , must satisfy the negative Pell equation . For example, for and , then,
:
:
and so on. Also, every even
In the more recent mathematical literature, uses the rectangle-counting interpretation of these numbers to form a geometric proof of the identity (see also ); he observes that it may also be proved easily (but uninformatively) by induction, and states that provides "an interesting old Arabic proof". provides a purely visual proof, provide two additional proofs, and gives seven geometric proofs.
For example, the sum of the first 5 cubes is the square of the 5th triangular number,
:
A similar result can be given for the sum of the first odd cubes,
:
but , must satisfy the negative Pell equation . For example, for and , then,
:
:
and so on. Also, every even perfect number
In number theory, a perfect number is a positive integer that is equal to the sum of its positive proper divisors, that is, divisors excluding the number itself. For instance, 6 has proper divisors 1, 2 and 3, and 1 + 2 + 3 = 6, so 6 is a perfec ...
, except the lowest, is the sum of the first odd cubes (''p'' = 3, 5, 7, ...):
:
:
:
Sum of cubes of numbers in arithmetic progression
arithmetic progression
An arithmetic progression or arithmetic sequence is a sequence of numbers such that the difference from any succeeding term to its preceding term remains constant throughout the sequence. The constant difference is called common difference of that ...
whose sum is a cube:
:
:
:
with the first one sometimes identified as the mysterious Plato's number. The formula for finding the sum of
cubes of numbers in arithmetic progression with common difference and initial cube ,
:
is given by
:
A parametric solution to
:
is known for the special case of , or consecutive cubes, as found by Pagliani in 1829.
Cubes as sums of successive odd integers
In the sequence of odd integers 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, ..., the first ''one'' is a cube (); the sum of the next ''two'' is the next cube (); the sum of the next ''three'' is the next cube (); and so forth.Waring's problem for cubes
Every positive integer can be written as the sum of nine (or fewer) positive cubes. This upper limit of nine cubes cannot be reduced because, for example, 23 cannot be written as the sum of fewer than nine positive cubes: :23 = 23 + 23 + 13 + 13 + 13 + 13 + 13 + 13 + 13.In rational numbers
Every positiverational number
In mathematics, a rational number is a number that can be expressed as the quotient or fraction of two integers, a numerator and a non-zero denominator . For example, is a rational number, as is every integer (for example,
The set of all ...
is the sum of three positive rational cubes, and there are rationals that are not the sum of two rational cubes.
In real numbers, other fields, and rings
Inreal number
In mathematics, a real number is a number that can be used to measure a continuous one- dimensional quantity such as a duration or temperature. Here, ''continuous'' means that pairs of values can have arbitrarily small differences. Every re ...
s, the cube function preserves the order: larger numbers have larger cubes. In other words, cubes (strictly) monotonically increase. Also, its codomain
In mathematics, a codomain, counter-domain, or set of destination of a function is a set into which all of the output of the function is constrained to fall. It is the set in the notation . The term '' range'' is sometimes ambiguously used to ...
is the entire real line
A number line is a graphical representation of a straight line that serves as spatial representation of numbers, usually graduated like a ruler with a particular origin (geometry), origin point representing the number zero and evenly spaced mark ...
: the function is a surjection
In mathematics, a surjective function (also known as surjection, or onto function ) is a function such that, for every element of the function's codomain, there exists one element in the function's domain such that . In other words, for a f ...
(takes all possible values). Only three numbers are equal to their own cubes: , , and . If or , then . If or , then . All aforementioned properties pertain also to any higher odd power (, , ...) of real numbers. Equalities and inequalities are also true in any ordered ring
In abstract algebra, an ordered ring is a (usually commutative) ring ''R'' with a total order ≤ such that for all ''a'', ''b'', and ''c'' in ''R'':
* if ''a'' ≤ ''b'' then ''a'' + ''c'' ≤ ''b'' + ''c''.
* if 0 ≤ ''a'' and 0 ≤ ''b'' th ...
.
Volumes of similar Euclidean solids are related as cubes of their linear sizes.
In complex number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the for ...
s, the cube of a purely imaginary number is also purely imaginary. For example, .
The derivative
In mathematics, the derivative is a fundamental tool that quantifies the sensitivity to change of a function's output with respect to its input. The derivative of a function of a single variable at a chosen input value, when it exists, is t ...
of equals .
Cubes ''occasionally'' have the surjective property in other fields, such as in for such prime that , but not necessarily: see the counterexample with rationals above. Also in only three elements 0, ±1 are perfect cubes, of seven total. −1, 0, and 1 are perfect cubes ''anywhere'' and the only elements of a field equal to their own cubes: .
History
Determination of the cubes of large numbers was very common in many ancient civilizations. Mesopotamian mathematicians created cuneiform tablets with tables for calculating cubes and cube roots by the Old Babylonian period (20th to 16th centuries BC). Cubic equations were known to theancient Greek
Ancient Greek (, ; ) includes the forms of the Greek language used in ancient Greece and the classical antiquity, ancient world from around 1500 BC to 300 BC. It is often roughly divided into the following periods: Mycenaean Greek (), Greek ...
mathematician Diophantus
Diophantus of Alexandria () (; ) was a Greek mathematician who was the author of the '' Arithmetica'' in thirteen books, ten of which are still extant, made up of arithmetical problems that are solved through algebraic equations.
Although Jose ...
. Hero of Alexandria
Hero of Alexandria (; , , also known as Heron of Alexandria ; probably 1st or 2nd century AD) was a Greek mathematician and engineer who was active in Alexandria in Egypt during the Roman era. He has been described as the greatest experimental ...
devised a method for calculating cube roots in the 1st century CE. Methods for solving cubic equations and extracting cube roots appear in ''The Nine Chapters on the Mathematical Art
''The Nine Chapters on the Mathematical Art'' is a Chinese mathematics book, composed by several generations of scholars from the 10th–2nd century BCE, its latest stage being from the 1st century CE. This book is one of the earliest surviving ...
'', a Chinese mathematical text compiled around the 2nd century BCE and commented on by Liu Hui
Liu Hui () was a Chinese mathematician who published a commentary in 263 CE on ''Jiu Zhang Suan Shu ( The Nine Chapters on the Mathematical Art).'' He was a descendant of the Marquis of Zixiang of the Eastern Han dynasty and lived in the state ...
in the 3rd century CE.
See also
* Cabtaxi number *Cubic equation
In algebra, a cubic equation in one variable is an equation of the form
ax^3+bx^2+cx+d=0
in which is not zero.
The solutions of this equation are called roots of the cubic function defined by the left-hand side of the equation. If all of th ...
* Doubling the cube
Doubling the cube, also known as the Delian problem, is an ancient geometry, geometric problem. Given the Edge (geometry), edge of a cube, the problem requires the construction of the edge of a second cube whose volume is double that of the first ...
* Eighth power
* Euler's sum of powers conjecture
* Fifth power
* Fourth power
* Kepler's laws of planetary motion#Third law
* Monkey saddle
* Perfect power
* Seventh power
* Sixth power
* Square
In geometry, a square is a regular polygon, regular quadrilateral. It has four straight sides of equal length and four equal angles. Squares are special cases of rectangles, which have four equal angles, and of rhombuses, which have four equal si ...
* Taxicab number
Notes
References
Sources
* * * * * * * * {{Series_(mathematics) Elementary arithmetic Figurate numbers Integer sequences Integers Number theory Unary operations