|
Fifth Power (algebra)
In arithmetic and algebra, the fifth power or sursolid of a number ''n'' is the result of multiplying five instances of ''n'' together: :. Fifth powers are also formed by multiplying a number by its fourth power, or the square of a number by its cube. The sequence of fifth powers of integers is: :0, 1, 32, 243, 1024, 3125, 7776, 16807, 32768, 59049, 100000, 161051, 248832, 371293, 537824, 759375, 1048576, 1419857, 1889568, 2476099, 3200000, 4084101, 5153632, 6436343, 7962624, 9765625, ... Properties For any integer ''n'', the last decimal digit of ''n''5 is the same as the last (decimal) digit of ''n'', i.e. : n \equiv n^5\pmod By the Abel–Ruffini theorem, there is no general algebraic formula (formula expressed in terms of radical expressions) for the solution of polynomial equations containing a fifth power of the unknown as their highest power. This is the lowest power for which this is true. See quintic equation, sextic equation, and septic equation. Along with the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arithmetic
Arithmetic is an elementary branch of mathematics that deals with numerical operations like addition, subtraction, multiplication, and division. In a wider sense, it also includes exponentiation, extraction of roots, and taking logarithms. Arithmetic systems can be distinguished based on the type of numbers they operate on. Integer arithmetic is about calculations with positive and negative integers. Rational number arithmetic involves operations on fractions of integers. Real number arithmetic is about calculations with real numbers, which include both rational and irrational numbers. Another distinction is based on the numeral system employed to perform calculations. Decimal arithmetic is the most common. It uses the basic numerals from 0 to 9 and their combinations to express numbers. Binary arithmetic, by contrast, is used by most computers and represents numbers as combinations of the basic numerals 0 and 1. Computer arithmetic deals with the specificities of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Septic Equation
In algebra, a septic equation is an equation of the form :ax^7+bx^6+cx^5+dx^4+ex^3+fx^2+gx+h=0,\, where . A septic function is a function of the form :f(x)=ax^7+bx^6+cx^5+dx^4+ex^3+fx^2+gx+h\, where . In other words, it is a polynomial of degree seven. If , then ''f'' is a sextic function (), quintic function (), etc. The equation may be obtained from the function by setting . The ''coefficients'' may be either integers, rational numbers, real numbers, complex numbers or, more generally, members of any field. Because they have an odd degree, septic functions appear similar to quintic and cubic functions when graphed, except they may possess additional local maxima and local minima (up to three maxima and three minima). The derivative of a septic function is a sextic function. Solvable septics Some seventh degree equations can be solved by factorizing into radicals, but other septics cannot. Évariste Galois developed techniques for determining whether a given equ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integer Sequences
In mathematics, an integer sequence is a sequence (i.e., an ordered list) of integers. An integer sequence may be specified ''explicitly'' by giving a formula for its ''n''th term, or ''implicitly'' by giving a relationship between its terms. For example, the sequence 0, 1, 1, 2, 3, 5, 8, 13, ... (the Fibonacci sequence) is formed by starting with 0 and 1 and then adding any two consecutive terms to obtain the next one: an implicit description . The sequence 0, 3, 8, 15, ... is formed according to the formula ''n''2 − 1 for the ''n''th term: an explicit definition. Alternatively, an integer sequence may be defined by a property which members of the sequence possess and other integers do not possess. For example, we can determine whether a given integer is a perfect number, , even though we do not have a formula for the ''n''th perfect number. Computable and definable sequences An integer sequence is computable if there exists an algorithm that, given '' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elementary Arithmetic
Elementary arithmetic is a branch of mathematics involving addition, subtraction, multiplication, and Division (mathematics), division. Due to its low level of abstraction, broad range of application, and position as the foundation of all mathematics, elementary arithmetic is generally the first branch of mathematics taught in schools. Numeral systems In numeral system, numeral systems, Numerical digit, digits are characters used to represent the value of numbers. An example of a numeral system is the predominantly used Hindu–Arabic numeral system, Indo-Arabic numeral system (0 to 9), which uses a Base 10, decimal positional notation. Other numeral systems include the Kaktovik numerals, Kaktovik system (often used in the Eskimo-Aleut languages of Alaska, Canada, and Greenland), and is a vigesimal positional notation system. Regardless of the numeral system used, the results of arithmetic operations are unaffected. Successor function and ordering In elementary arithmetic, the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Number Theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers and arithmetic functions. Number theorists study prime numbers as well as the properties of mathematical objects constructed from integers (for example, rational numbers), or defined as generalizations of the integers (for example, algebraic integers). Integers can be considered either in themselves or as solutions to equations (Diophantine geometry). Questions in number theory can often be understood through the study of Complex analysis, analytical objects, such as the Riemann zeta function, that encode properties of the integers, primes or other number-theoretic objects in some fashion (analytic number theory). One may also study real numbers in relation to rational numbers, as for instance how irrational numbers can be approximated by fractions (Diophantine approximation). Number theory is one of the oldest branches of mathematics alongside geometry. One quirk of number theory is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integers
An integer is the number zero (0), a positive natural number (1, 2, 3, ...), or the negation of a positive natural number (−1, −2, −3, ...). The negations or additive inverses of the positive natural numbers are referred to as negative integers. The set (mathematics), set of all integers is often denoted by the boldface or blackboard bold The set of natural numbers \mathbb is a subset of \mathbb, which in turn is a subset of the set of all rational numbers \mathbb, itself a subset of the real numbers \mathbb. Like the set of natural numbers, the set of integers \mathbb is Countable set, countably infinite. An integer may be regarded as a real number that can be written without a fraction, fractional component. For example, 21, 4, 0, and −2048 are integers, while 9.75, , 5/4, and Square root of 2, are not. The integers form the smallest Group (mathematics), group and the smallest ring (mathematics), ring containing the natural numbers. In algebraic number theory, the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
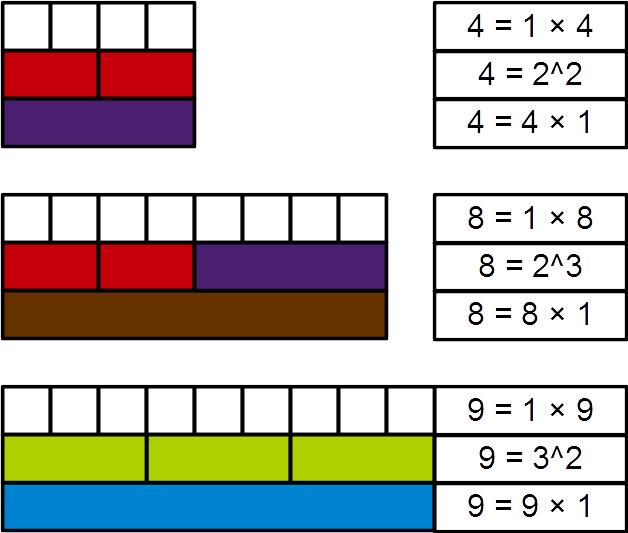
Perfect Power
In mathematics, a perfect power is a natural number that is a product of equal natural factors, or, in other words, an integer that can be expressed as a square or a higher integer power of another integer greater than one. More formally, ''n'' is a perfect power if there exist natural numbers ''m'' > 1, and ''k'' > 1 such that ''mk'' = ''n''. In this case, ''n'' may be called a perfect ''k''th power. If ''k'' = 2 or ''k'' = 3, then ''n'' is called a perfect square or perfect cube, respectively. Sometimes 0 and 1 are also considered perfect powers (0''k'' = 0 for any ''k'' > 0, 1''k'' = 1 for any ''k''). Examples and sums A sequence of perfect powers can be generated by iterating through the possible values for ''m'' and ''k''. The first few ascending perfect powers in numerical order (showing duplicate powers) are : : 2^2 = 4,\ 2^3 = 8,\ 3^2 = 9,\ 2^4 = 16,\ 4^2 = 16,\ 5^2 = 25,\ 3^3 = 27, 2^5 = 32,\ 6^2 = 36,\ 7^2 = 49,\ 2^6 = 64,\ 4^3 = 64,\ 8^2 = 64, \dots The sum o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square (algebra)
In mathematics, a square is the result of multiplying a number by itself. The verb "to square" is used to denote this operation. Squaring is the same as raising to the power 2, and is denoted by a superscript 2; for instance, the square of 3 may be written as 32, which is the number 9. In some cases when superscripts are not available, as for instance in programming languages or plain text files, the notations ''x''^2 ( caret) or ''x''**2 may be used in place of ''x''2. The adjective which corresponds to squaring is '' quadratic''. The square of an integer may also be called a '' square number'' or a ''perfect square''. In algebra, the operation of squaring is often generalized to polynomials, other expressions, or values in systems of mathematical values other than the numbers. For instance, the square of the linear polynomial is the quadratic polynomial . One of the important properties of squaring, for numbers as well as in many other mathematical systems, is that ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cube (algebra)
In arithmetic and algebra, the cube of a number is its third exponentiation, power, that is, the result of multiplying three instances of together. The cube of a number is denoted , using a superscript 3, for example . The cube Mathematical operation, operation can also be defined for any other expression (mathematics), mathematical expression, for example . The cube is also the number multiplied by its square (algebra), square: :. The ''cube function'' is the function (mathematics), function (often denoted ) that maps a number to its cube. It is an odd function, as :. The volume of a Cube (geometry), geometric cube is the cube of its side length, giving rise to the name. The Inverse function, inverse operation that consists of finding a number whose cube is is called extracting the cube root of . It determines the side of the cube of a given volume. It is also raised to the one-third power. The graph of a function, graph of the cube function is known as the cubic para ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fourth Power
In arithmetic and algebra, the fourth power of a number ''n'' is the result of multiplying four instances of ''n'' together. So: :''n''4 = ''n'' × ''n'' × ''n'' × ''n'' Fourth powers are also formed by multiplying a number by its cube. Furthermore, they are squares of squares. Some people refer to ''n''4 as n '' tesseracted'', '' hypercubed'', '' zenzizenzic'', '' biquadrate'' or ''supercubed'' instead of “to the power of 4”. The sequence of fourth powers of integers, known as biquadrates or tesseractic numbers, is: :0, 1, 16, 81, 256, 625, 1296, 2401, 4096, 6561, 10000, 14641, 20736, 28561, 38416, 50625, 65536, 83521, 104976, 130321, 160000, 194481, 234256, 279841, 331776, 390625, 456976, 531441, 614656, 707281, 810000, ... . Properties The last digit of a fourth power in decimal can only be 0, 1, 5, or 6. In hexadecimal the last nonzero digit of a fourth power is always 1.An odd fourth power is the square of an odd square number. All odd squares are congruent to 1 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sixth Power
In arithmetic and algebra the sixth power of a number ''n'' is the result of multiplying six instances of ''n'' together. So: :. Sixth powers can be formed by multiplying a number by its fifth power, multiplying the square of a number by its fourth power, by cubing a square, or by squaring a cube. The sequence of sixth powers of integers are: :0, 1, 64, 729, 4096, 15625, 46656, 117649, 262144, 531441, 1000000, 1771561, 2985984, 4826809, 7529536, 11390625, 16777216, 24137569, 34012224, 47045881, 64000000, 85766121, 113379904, 148035889, 191102976, 244140625, 308915776, 387420489, 481890304, ... They include the significant decimal numbers 106 (a million), 1006 (a short-scale trillion and long-scale billion), 10006 (a quintillion and a long-scale trillion) and so on. Squares and cubes The sixth powers of integers can be characterized as the numbers that are simultaneously squares and cubes. In this way, they are analogous to two other classes of figurate numbers: the square t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Seventh Power
Seventh is the ordinal form of the number seven. Seventh may refer to: * Seventh Amendment to the United States Constitution * A fraction (mathematics), , equal to one of seven equal parts Film and television *"The Seventh", a second-season episode of ''Star Trek: Enterprise'' Music * A seventh (interval), the difference between two pitches ** Diminished seventh, a chromatically reduced minor seventh interval ** Major seventh, the larger of two commonly occurring musical intervals that span seven diatonic scale degrees ** Minor seventh, the smaller of two commonly occurring musical intervals that span seven diatonic scale degrees ** Harmonic seventh, the interval of exactly 4:7, whose approximation to the minor seventh in equal temperament explains the "sweetness" of the dominant seventh chord in a major key ** Augmented seventh, an interval * Leading-tone or subtonic, the seventh degree and the chord built on the seventh degree * Seventh chord, a chord consisting of a triad plu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |