Condensed Matter Physicist

Condensed matter physics is the field of physics that deals with the macroscopic and microscopic physical properties of matter, especially the solid and liquid phases, that arise from electromagnetic forces between atoms and electrons. More generally, the subject deals with condensed phases of matter: systems of many constituents with strong interactions among them. More exotic condensed phases include the superconducting phase exhibited by certain materials at extremely low cryogenic temperatures, the ferromagnetic and antiferromagnetic phases of spins on crystal lattices of atoms, the Bose–Einstein condensates found in ultracold atomic systems, and liquid crystals. Condensed matter physicists seek to understand the behavior of these phases by experiments to measure various material properties, and by applying the physical laws of quantum mechanics, electromagnetism, statistical mechanics, and other physics theories to develop mathematical models and predict the properties of extremely large groups of atoms.

The diversity of systems and phenomena available for study makes condensed matter physics the most active field of contemporary physics: one third of all American physicists self-identify as condensed matter physicists, and the Division of Condensed Matter Physics is the largest division of the American Physical Society. These include solid state and soft matter physicists, who study quantum and non-quantum physical properties of matter respectively. Both types study a great range of materials, providing many research, funding and employment opportunities. The field overlaps with chemistry, materials science, engineering and nanotechnology, and relates closely to atomic physics and biophysics. The theoretical physics of condensed matter shares important concepts and methods with that of particle physics and nuclear physics.

A variety of topics in physics such as crystallography, metallurgy, elasticity, magnetism, etc., were treated as distinct areas until the 1940s, when they were grouped together as ''solid-state physics''. Around the 1960s, the study of physical properties of liquids was added to this list, forming the basis for the more comprehensive specialty of condensed matter physics. The Bell Telephone Laboratories was one of the first institutes to conduct a research program in condensed matter physics. According to the founding director of the Max Planck Institute for Solid State Research, physics professor Manuel Cardona, it was Albert Einstein who created the modern field of condensed matter physics starting with his seminal 1905 article on the photoelectric effect and photoluminescence which opened the fields of photoelectron spectroscopy and photoluminescence spectroscopy, and later his 1907 article on the specific heat of solids which introduced, for the first time, the effect of lattice vibrations on the thermodynamic properties of crystals, in particular the specific heat. Deputy Director of the Yale Quantum Institute A. Douglas Stone makes a similar priority case for Einstein in his work on the synthetic history of quantum mechanics.

Etymology

According to physicist Philip Warren Anderson, the use of the term "condensed matter" to designate a field of study was coined by him and Volker Heine, when they changed the name of their group at the Cavendish Laboratories, Cambridge, from ''Solid state theory'' to ''Theory of Condensed Matter'' in 1967, as they felt it better included their interest in liquids, nuclear matter, and so on. Although Anderson and Heine helped popularize the name "condensed matter", it had been used in Europe for some years, most prominently in the Springer-Verlag journal ''Physics of Condensed Matter'', launched in 1963. The name "condensed matter physics" emphasized the commonality of scientific problems encountered by physicists working on solids, liquids, plasmas, and other complex matter, whereas "solid state physics" was often associated with restricted industrial applications of metals and semiconductors. In the 1960s and 70s, some physicists felt the more comprehensive name better fit the funding environment and Cold War politics of the time.

References to "condensed" states can be traced to earlier sources. For example, in the introduction to his 1947 book ''Kinetic Theory of Liquids'', Yakov Frenkel proposed that "The kinetic theory of liquids must accordingly be developed as a generalization and extension of the kinetic theory of solid bodies. As a matter of fact, it would be more correct to unify them under the title of 'condensed bodies.

History

Classical physics

One of the first studies of condensed states of matter was by English chemist Humphry Davy, in the first decades of the nineteenth century. Davy observed that of the forty chemical elements known at the time, twenty-six had metallic properties such as lustre, ductility and high electrical and thermal conductivity. This indicated that the atoms in John Dalton's atomic theory were not indivisible as Dalton claimed, but had inner structure. Davy further claimed that elements that were then believed to be gases, such as nitrogen and hydrogen could be liquefied under the right conditions and would then behave as metals.

In 1823, Michael Faraday, then an assistant in Davy's lab, successfully liquefied chlorine and went on to liquefy all known gaseous elements, except for nitrogen, hydrogen, and oxygen. Shortly after, in 1869, Irish chemist Thomas Andrews studied the phase transition from a liquid to a gas and coined the term critical point to describe the condition where a gas and a liquid were indistinguishable as phases, and Dutch physicist Johannes van der Waals supplied the theoretical framework which allowed the prediction of critical behavior based on measurements at much higher temperatures. By 1908, James Dewar and Heike Kamerlingh Onnes were successfully able to liquefy hydrogen and the then newly discovered helium respectively.

Paul Drude in 1900 proposed the first theoretical model for a classical electron moving through a metallic solid. Drude's model described properties of metals in terms of a gas of free electrons, and was the first microscopic model to explain empirical observations such as the Wiedemann–Franz law. However, despite the success of Drude's model, it had one notable problem: it was unable to correctly explain the electronic contribution to the specific heat and magnetic properties of metals, and the temperature dependence of resistivity at low temperatures.

In 1911, three years after helium was first liquefied, Onnes working at University of Leiden discovered superconductivity in mercury, when he observed the electrical resistivity of mercury to vanish at temperatures below a certain value. The phenomenon completely surprised the best theoretical physicists of the time, and it remained unexplained for several decades. Albert Einstein, in 1922, said regarding contemporary theories of superconductivity that "with our far-reaching ignorance of the quantum mechanics of composite systems we are very far from being able to compose a theory out of these vague ideas."

Advent of quantum mechanics

Drude's classical model was augmented by Wolfgang Pauli, Arnold Sommerfeld, Felix Bloch and other physicists. Pauli realized that the free electrons in metal must obey the Fermi–Dirac statistics. Using this idea, he developed the theory of paramagnetism in 1926. Shortly after, Sommerfeld incorporated the Fermi–Dirac statistics into the free electron model and made it better to explain the heat capacity. Two years later, Bloch used quantum mechanics to describe the motion of an electron in a periodic lattice.

The mathematics of crystal structures developed by Auguste Bravais, Yevgraf Fyodorov and others was used to classify crystals by their symmetry group, and tables of crystal structures were the basis for the series ''International Tables of Crystallography'', first published in 1935. Band structure calculations were first used in 1930 to predict the properties of new materials, and in 1947 John Bardeen, Walter Brattain and William Shockley developed the first semiconductor-based transistor, heralding a revolution in electronics.

In 1879, Edwin Herbert Hall working at the Johns Hopkins University discovered that a voltage developed across conductors which was transverse to both an electric current in the conductor and a magnetic field applied perpendicular to the current. This phenomenon, arising due to the nature of charge carriers in the conductor, came to be termed the Hall effect, but it was not properly explained at the time because the electron was not experimentally discovered until 18 years later. After the advent of quantum mechanics, Lev Landau in 1930 developed the theory of Landau quantization and laid the foundation for a theoretical explanation of the quantum Hall effect which was discovered half a century later.

Magnetism as a property of matter has been known in China since 4000 BC. However, the first modern studies of magnetism only started with the development of electrodynamics by Faraday, Maxwell and others in the nineteenth century, which included classifying materials as ferromagnetic, paramagnetic and diamagnetic based on their response to magnetization. Pierre Curie studied the dependence of magnetization on temperature and discovered the Curie point phase transition in ferromagnetic materials. In 1906, Pierre Weiss introduced the concept of magnetic domains to explain the main properties of ferromagnets. The first attempt at a microscopic description of magnetism was by Wilhelm Lenz and Ernst Ising through the Ising model that described magnetic materials as consisting of a periodic lattice of spins that collectively acquired magnetization. The Ising model was solved exactly to show that spontaneous magnetization can occur in one dimension and it is possible in higher-dimensional lattices. Further research such as by Bloch on spin waves and Néel on antiferromagnetism led to developing new magnetic materials with applications to magnetic storage devices.

Modern many-body physics

The Sommerfeld model and spin models for ferromagnetism illustrated the successful application of quantum mechanics to condensed matter problems in the 1930s. However, there still were several unsolved problems, most notably the description of superconductivity and the Kondo effect. After World War II, several ideas from quantum field theory were applied to condensed matter problems. These included recognition of collective excitation modes of solids and the important notion of a quasiparticle. Soviet physicist Lev Landau used the idea for the Fermi liquid theory wherein low energy properties of interacting fermion systems were given in terms of what are now termed Landau-quasiparticles. Landau also developed a mean-field theory for continuous phase transitions, which described ordered phases as spontaneous breakdown of symmetry. The theory also introduced the notion of an order parameter to distinguish between ordered phases. Eventually in 1956, John Bardeen, Leon Cooper and Robert Schrieffer developed the so-called BCS theory of superconductivity, based on the discovery that arbitrarily small attraction between two electrons of opposite spin mediated by phonons in the lattice can give rise to a bound state called a Cooper pair.

The study of phase transitions and the critical behavior of observables, termed critical phenomena, was a major field of interest in the 1960s. Leo Kadanoff, Benjamin Widom and Michael Fisher developed the ideas of critical exponents and widom scaling. These ideas were unified by Kenneth G. Wilson in 1972, under the formalism of the renormalization group in the context of quantum field theory.

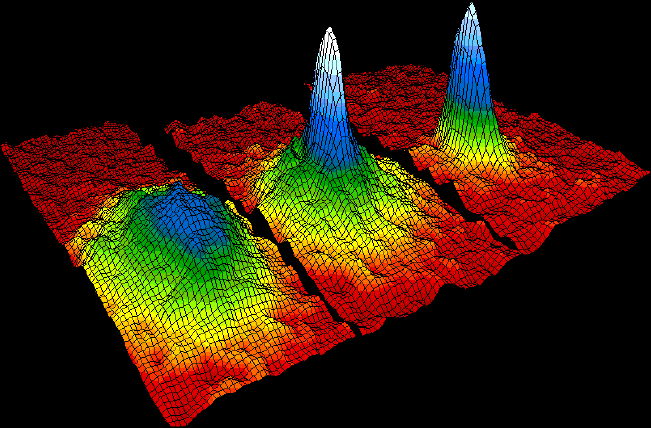
The quantum Hall effect was discovered by Klaus von Klitzing, Dorda and Pepper in 1980 when they observed the Hall conductance to be integer multiples of a fundamental constant $e^2/h$.(see figure) The effect was observed to be independent of parameters such as system size and impurities. In 1981, theorist Robert Laughlin proposed a theory explaining the unanticipated precision of the integral plateau. It also implied that the Hall conductance is proportional to a topological invariant, called Chern number, whose relevance for the band structure of solids was formulated by David J. Thouless and collaborators. Shortly after, in 1982, Horst Störmer and Daniel Tsui observed the fractional quantum Hall effect where the conductance was now a rational multiple of the constant $e^2/h$. Laughlin, in 1983, realized that this was a consequence of quasiparticle interaction in the Hall states and formulated a variational method solution, named the Laughlin wavefunction. The study of topological properties of the fractional Hall effect remains an active field of research. Decades later, the aforementioned topological band theory advanced by David J. Thouless and collaborators was further expanded leading to the discovery of topological insulators.

In 1986, Karl Müller and Johannes Bednorz discovered the first high temperature superconductor, La_2-xBa_xCuO₄, which is superconducting at temperatures as high as 39 kelvin. It was realized that the high temperature superconductors are examples of strongly correlated materials where the electron–electron interactions play an important role. A satisfactory theoretical description of high-temperature superconductors is still not known and the field of strongly correlated materials continues to be an active research topic.

In 2012, several groups released preprints which suggest that samarium hexaboride has the properties of a topological insulator in accord with the earlier theoretical predictions. Since samarium hexaboride is an established Kondo insulator, i.e. a strongly correlated electron material, it is expected that the existence of a topological Dirac surface state in this material would lead to a topological insulator with strong electronic correlations.

Theoretical

Theoretical condensed matter physics involves the use of theoretical models to understand properties of states of matter. These include models to study the electronic properties of solids, such as the Drude model, the band structure and the density functional theory. Theoretical models have also been developed to study the physics of phase transitions, such as the Ginzburg–Landau theory, critical exponents and the use of mathematical methods of quantum field theory and the renormalization group. Modern theoretical studies involve the use of numerical computation of electronic structure and mathematical tools to understand phenomena such as high-temperature superconductivity, topological phases, and gauge symmetries.

Emergence

Theoretical understanding of condensed matter physics is closely related to the notion of emergence, wherein complex assemblies of particles behave in ways dramatically different from their individual constituents. For example, a range of phenomena related to high temperature superconductivity are understood poorly, although the microscopic physics of individual electrons and lattices is well known. Similarly, models of condensed matter systems have been studied where collective excitations behave like photons and electrons, thereby describing electromagnetism as an emergent phenomenon. Emergent properties can also occur at the interface between materials: one example is the lanthanum aluminate-strontium titanate interface, where two band-insulators are joined to create conductivity and superconductivity.

Electronic theory of solids

The metallic state has historically been an important building block for studying properties of solids. The first theoretical description of metals was given by Paul Drude in 1900 with the Drude model, which explained electrical and thermal properties by describing a metal as an ideal gas of then-newly discovered electrons. He was able to derive the empirical Wiedemann-Franz law and get results in close agreement with the experiments. This classical model was then improved by Arnold Sommerfeld who incorporated the Fermi–Dirac statistics of electrons and was able to explain the anomalous behavior of the specific heat of metals in the Wiedemann–Franz law. In 1912, The structure of crystalline solids was studied by Max von Laue and Paul Knipping, when they observed the X-ray diffraction pattern of crystals, and concluded that crystals get their structure from periodic lattices of atoms. In 1928, Swiss physicist Felix Bloch provided a wave function solution to the Schrödinger equation with a periodic potential, known as Bloch's theorem.

Calculating electronic properties of metals by solving the many-body wavefunction is often computationally hard, and hence, approximation methods are needed to obtain meaningful predictions. The Thomas–Fermi theory, developed in the 1920s, was used to estimate system energy and electronic density by treating the local electron density as a variational parameter. Later in the 1930s, Douglas Hartree, Vladimir Fock and John Slater developed the so-called Hartree–Fock wavefunction as an improvement over the Thomas–Fermi model. The Hartree–Fock method accounted for exchange statistics of single particle electron wavefunctions. In general, it is very difficult to solve the Hartree–Fock equation. Only the free electron gas case can be solved exactly. Finally in 1964–65, Walter Kohn, Pierre Hohenberg and Lu Jeu Sham proposed the density functional theory (DFT) which gave realistic descriptions for bulk and surface properties of metals. The density functional theory has been widely used since the 1970s for band structure calculations of variety of solids.

Symmetry breaking

Some states of matter exhibit ''symmetry breaking'', where the relevant laws of physics possess some form of symmetry that is broken. A common example is crystalline solids, which break continuous translational symmetry. Other examples include magnetized ferromagnets, which break rotational symmetry, and more exotic states such as the ground state of a BCS superconductor, that breaks U(1) phase rotational symmetry.

Goldstone's theorem in quantum field theory states that in a system with broken continuous symmetry, there may exist excitations with arbitrarily low energy, called the Goldstone bosons. For example, in crystalline solids, these correspond to phonons, which are quantized versions of lattice vibrations.

Phase transition

Phase transition refers to the change of phase of a system, which is brought about by change in an external parameter such as temperature, pressure, or molar composition. In a single-component system, a classical phase transition occurs at a temperature (at a specific pressure) where there is an abrupt change in the order of the system. For example, when ice melts and becomes water, the ordered hexagonal crystal structure of ice is modified to a hydrogen bonded, mobile arrangement of water molecules.

In quantum phase transitions, the temperature is set to absolute zero, and the non-thermal control parameter, such as pressure or magnetic field, causes the phase transitions when order is destroyed by quantum fluctuations originating from the Heisenberg uncertainty principle. Here, the different quantum phases of the system refer to distinct ground states of the Hamiltonian matrix. Understanding the behavior of quantum phase transition is important in the difficult tasks of explaining the properties of rare-earth magnetic insulators, high-temperature superconductors, and other substances.

Two classes of phase transitions occur: ''first-order transitions'' and ''second-order'' or ''continuous transitions''. For the latter, the two phases involved do not co-exist at the transition temperature, also called the critical point. Near the critical point, systems undergo critical behavior, wherein several of their properties such as correlation length, specific heat, and magnetic susceptibility diverge exponentially. These critical phenomena present serious challenges to physicists because normal macroscopic laws are no longer valid in the region, and novel ideas and methods must be invented to find the new laws that can describe the system.

The simplest theory that can describe continuous phase transitions is the Ginzburg–Landau theory, which works in the so-called mean-field approximation. However, it can only roughly explain continuous phase transition for ferroelectrics and type I superconductors which involves long range microscopic interactions. For other types of systems that involves short range interactions near the critical point, a better theory is needed.

Near the critical point, the fluctuations happen over broad range of size scales while the feature of the whole system is scale invariant. Renormalization group methods successively average out the shortest wavelength fluctuations in stages while retaining their effects into the next stage. Thus, the changes of a physical system as viewed at different size scales can be investigated systematically. The methods, together with powerful computer simulation, contribute greatly to the explanation of the critical phenomena associated with continuous phase transition.

Experimental

Experimental condensed matter physics involves the use of experimental probes to try to discover new properties of materials. Such probes include effects of electric and magnetic fields, measuring response functions, transport properties and thermometry. Commonly used experimental methods include spectroscopy, with probes such as X-rays, infrared light and inelastic neutron scattering; study of thermal response, such as specific heat and measuring transport via thermal and heat conduction.

Scattering

Several condensed matter experiments involve scattering of an experimental probe, such as X-ray, optical photons, neutrons, etc., on constituents of a material. The choice of scattering probe depends on the observation energy scale of interest. Visible light has energy on the scale of 1 electron volt (eV) and is used as a scattering probe to measure variations in material properties such as the dielectric constant and refractive index. X-rays have energies of the order of 10 keV and hence are able to probe atomic length scales, and are used to measure variations in electron charge density and crystal structure.

Neutrons can also probe atomic length scales and are used to study the scattering off nuclei and electron spins and magnetization (as neutrons have spin but no charge). Coulomb and Mott scattering measurements can be made by using electron beams as scattering probes. Similarly, positron annihilation can be used as an indirect measurement of local electron density. Laser spectroscopy is an excellent tool for studying the microscopic properties of a medium, for example, to study forbidden transitions in media with nonlinear optical spectroscopy.

External magnetic fields

In experimental condensed matter physics, external magnetic fields act as thermodynamic variables that control the state, phase transitions and properties of material systems. Nuclear magnetic resonance (NMR) is a method by which external magnetic fields are used to find resonance modes of individual nuclei, thus giving information about the atomic, molecular, and bond structure of their environment. NMR experiments can be made in magnetic fields with strengths up to 60 tesla. Higher magnetic fields can improve the quality of NMR measurement data. Quantum oscillations is another experimental method where high magnetic fields are used to study material properties such as the geometry of the Fermi surface. High magnetic fields will be useful in experimental testing of the various theoretical predictions such as the quantized magnetoelectric effect, image magnetic monopole, and the half-integer quantum Hall effect.

Magnetic resonance spectroscopy

The local structure, as well as the structure of the nearest neighbour atoms, can be investigated in condensed matter with magnetic resonance methods, such as electron paramagnetic resonance (EPR) and nuclear magnetic resonance (NMR), which are very sensitive to the details of the surrounding of nuclei and electrons by means of the hyperfine coupling. Both localized electrons and specific stable or unstable isotopes of the nuclei become the probe of these hyperfine interactions), which couple the electron or nuclear spin to the local electric and magnetic fields. These methods are suitable to study defects, diffusion, phase transitions and magnetic order. Common experimental methods include NMR, nuclear quadrupole resonance (NQR), implanted radioactive probes as in the case of muon spin spectroscopy ($\mu$SR), Mössbauer spectroscopy, $\beta$NMR and perturbed angular correlation (PAC). PAC is especially ideal for the study of phase changes at extreme temperatures above 2000 °C due to the temperature independence of the method.

Cold atomic gases

Ultracold atom trapping in optical lattices is an experimental tool commonly used in condensed matter physics, and in atomic, molecular, and optical physics. The method involves using optical lasers to form an interference pattern, which acts as a ''lattice'', in which ions or atoms can be placed at very low temperatures. Cold atoms in optical lattices are used as ''quantum simulators'', that is, they act as controllable systems that can model behavior of more complicated systems, such as frustrated magnets. In particular, they are used to engineer one-, two- and three-dimensional lattices for a Hubbard model with pre-specified parameters, and to study phase transitions for antiferromagnetic and spin liquid ordering.

In 1995, a gas of rubidium atoms cooled down to a temperature of 170 nK was used to experimentally realize the Bose–Einstein condensate, a novel state of matter originally predicted by S. N. Bose and Albert Einstein, wherein a large number of atoms occupy one quantum state.

Applications

Research in condensed matter physics has given rise to several device applications, such as the development of the semiconductor transistor, laser technology, magnetic storage, liquid crystals, optical fibres and several phenomena studied in the context of nanotechnology. Methods such as scanning-tunneling microscopy can be used to control processes at the nanometer scale, and have given rise to the study of nanofabrication. Such molecular machines were developed for example by Nobel laureates in chemistry Ben Feringa, Jean-Pierre Sauvage and Fraser Stoddart. Feringa and his team developed multiple molecular machines such as the molecular car, molecular windmill and many more.

In quantum computation, information is represented by quantum bits, or qubits. The qubits may decohere quickly before useful computation is completed. This serious problem must be solved before quantum computing may be realized. To solve this problem, several promising approaches are proposed in condensed matter physics, including Josephson junction qubits, spintronic qubits using the spin orientation of magnetic materials, and the topological non-Abelian anyons from fractional quantum Hall effect states.

Condensed matter physics also has important uses for biomedicine. For example, magnetic resonance imaging is widely used in medical imaging of soft tissue and other physiological features which cannot be viewed with traditional x-ray imaging.

See also

*
*
*
*
*
*
*
*
*
*

Notes

References

Further reading

* Anderson, Philip W. (2018-03-09). ''Basic Notions Of Condensed Matter Physics''. CRC Press. .
*Girvin, Steven M.; Yang, Kun (2019-02-28). ''Modern Condensed Matter Physics''. Cambridge University Press. .
*Coleman, Piers (2015). '' Introduction to Many-Body Physics'', Cambridge University Press, .
*P. M. Chaikin and T. C. Lubensky (2000). ''Principles of Condensed Matter Physics'', Cambridge University Press; 1st edition,
* Alexander Altland and Ben Simons (2006). ''Condensed Matter Field Theory'', Cambridge University Press, .
* Michael P. Marder (2010). ''Condensed Matter Physics, second edition'', John Wiley and Sons, .
*Lillian Hoddeson, Ernest Braun, Jürgen Teichmann and Spencer Weart, eds. (1992). ''Out of the Crystal Maze: Chapters from the History of Solid State Physics'', Oxford University Press, .

External links

*

{{DEFAULTSORT:Condensed Matter Physics

Materials science