 |
Landau Quantization
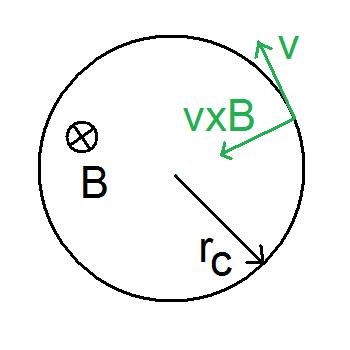
In quantum mechanics, the energies of Cyclotron motion#Cyclotron resonance, cyclotron orbits of charged particles in a uniform magnetic field are quantized to discrete values, thus known as Landau levels. These levels are Degenerate energy level, degenerate, with the number of electrons per level directly proportional to the strength of the applied magnetic field. It is named after the Soviet physicist Lev Landau. Landau quantization contributes towards magnetic susceptibility of metals, known as Landau diamagnetism. Under strong magnetic fields, Landau quantization leads to oscillations in electronic properties of materials as a function of the applied magnetic field known as the De Haas–Van Alphen effect, De Haas–Van Alphen and Shubnikov–de Haas effects. Landau quantization is a key ingredient in explanation of the Quantum Hall effect, integer quantum Hall effect. Derivation Consider a system of non-interacting particles with charge and spin confined to an area in th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
 |
Quantum Mechanics
Quantum mechanics is the fundamental physical Scientific theory, theory that describes the behavior of matter and of light; its unusual characteristics typically occur at and below the scale of atoms. Reprinted, Addison-Wesley, 1989, It is the foundation of all quantum physics, which includes quantum chemistry, quantum field theory, quantum technology, and quantum information science. Quantum mechanics can describe many systems that classical physics cannot. Classical physics can describe many aspects of nature at an ordinary (macroscopic and Microscopic scale, (optical) microscopic) scale, but is not sufficient for describing them at very small submicroscopic (atomic and subatomic) scales. Classical mechanics can be derived from quantum mechanics as an approximation that is valid at ordinary scales. Quantum systems have Bound state, bound states that are Quantization (physics), quantized to Discrete mathematics, discrete values of energy, momentum, angular momentum, and ot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
Gauge Invariance
In physics, a gauge theory is a type of field theory in which the Lagrangian, and hence the dynamics of the system itself, does not change under local transformations according to certain smooth families of operations (Lie groups). Formally, the Lagrangian is invariant under these transformations. The term "gauge" refers to any specific mathematical formalism to regulate redundant degrees of freedom in the Lagrangian of a physical system. The transformations between possible gauges, called gauge transformations, form a Lie group—referred to as the '' symmetry group'' or the gauge group of the theory. Associated with any Lie group is the Lie algebra of group generators. For each group generator there necessarily arises a corresponding field (usually a vector field) called the gauge field. Gauge fields are included in the Lagrangian to ensure its invariance under the local group transformations (called gauge invariance). When such a theory is quantized, the quanta of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
 |
Dirac Cone
In physics, Dirac cones are features that occur in some electronic band structures that describe unusual electron transport properties of materials like graphene and topological insulators. In these materials, at energies near the Fermi level, the valence band and conduction band take the shape of the upper and lower halves of a conical surface, meeting at what are called Dirac points. Typical examples include graphene, topological insulators, bismuth antimony thin films and some other novel nanomaterials, in which the electronic energy and momentum have a linear dispersion relation such that the electronic band structure near the Fermi level takes the shape of an upper conical surface for the electrons and a lower conical surface for the holes. The two conical surfaces touch each other and form a zero-band gap semimetal. The name of Dirac cone comes from the Dirac equation that can describe relativistic particles in quantum mechanics, proposed by Paul Dirac. Isotropic Dira ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
 |
Graphene
Graphene () is a carbon allotrope consisting of a Single-layer materials, single layer of atoms arranged in a hexagonal lattice, honeycomb planar nanostructure. The name "graphene" is derived from "graphite" and the suffix -ene, indicating the presence of double bonds within the carbon structure. Graphene is known for its exceptionally high Ultimate tensile strength, tensile strength, Electrical resistivity and conductivity, electrical conductivity, Transparency and translucency, transparency, and being the thinnest two-dimensional material in the world. Despite the nearly transparent nature of a single graphene sheet, graphite (formed from stacked layers of graphene) appears black because it absorbs all visible light wavelengths. On a microscopic scale, graphene is the strongest material ever measured. The existence of graphene was first theorized in 1947 by P. R. Wallace, Philip R. Wallace during his research on graphite's electronic properties, while the term ''graphen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
 |
Single-layer Materials
In materials science, the term single-layer materials or 2D materials refers to crystalline solids consisting of a single layer of atoms. These materials are promising for some applications but remain the focus of research. Single-layer materials derived from single elements generally carry the -ene suffix in their names, e.g. graphene. Single-layer materials that are compounds of two or more elements have -ane or -ide suffixes. 2D materials can generally be categorized as either 2D allotropes of various elements or as compounds (consisting of two or more covalently bonding elements). It is predicted that there are hundreds of stable single-layer materials. The atomic structure and calculated basic properties of these and many other potentially synthesisable single-layer materials, can be found in computational databases. 2D materials can be produced using mainly two approaches: top-down exfoliation and bottom-up synthesis. The exfoliation methods include sonication, mechanical, h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
Dirac Equation
In particle physics, the Dirac equation is a relativistic wave equation derived by British physicist Paul Dirac in 1928. In its free form, or including electromagnetic interactions, it describes all spin-1/2 massive particles, called "Dirac particles", such as electrons and quarks for which parity is a symmetry. It is consistent with both the principles of quantum mechanics and the theory of special relativity, and was the first theory to account fully for special relativity in the context of quantum mechanics. The equation is validated by its rigorous accounting of the observed fine structure of the hydrogen spectrum and has become vital in the building of the Standard Model. The equation also implied the existence of a new form of matter, '' antimatter'', previously unsuspected and unobserved and which was experimentally confirmed several years later. It also provided a ''theoretical'' justification for the introduction of several component wave functions in Pauli' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
 |
Graphene - Geim - Landau Levels
Graphene () is a carbon allotrope consisting of a Single-layer materials, single layer of atoms arranged in a hexagonal lattice, honeycomb planar nanostructure. The name "graphene" is derived from "graphite" and the suffix -ene, indicating the presence of double bonds within the carbon structure. Graphene is known for its exceptionally high Ultimate tensile strength, tensile strength, Electrical resistivity and conductivity, electrical conductivity, Transparency and translucency, transparency, and being the thinnest two-dimensional material in the world. Despite the nearly transparent nature of a single graphene sheet, graphite (formed from stacked layers of graphene) appears black because it absorbs all visible light wavelengths. On a microscopic scale, graphene is the strongest material ever measured. The existence of graphene was first theorized in 1947 by P. R. Wallace, Philip R. Wallace during his research on graphite's electronic properties, while the term ''graphen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
 |
Zeeman Effect
The Zeeman effect () is the splitting of a spectral line into several components in the presence of a static magnetic field. It is caused by the interaction of the magnetic field with the magnetic moment of the atomic electron associated with its Angular momentum, orbital motion and Spin (physics), spin; this interaction shifts some orbital energies more than others, resulting in the split spectrum. The effect is named after the Netherlands, Dutch physicist Pieter Zeeman, who discovered it in 1896 and received a Nobel Prize in Physics for this discovery. It is analogous to the Stark effect, the splitting of a spectral line into several components in the presence of an electric field. Also, similar to the Stark effect, transitions between different components have, in general, different intensities, with some being entirely forbidden (in the dipole approximation), as governed by the selection rules. Since the distance between the Zeeman sub-levels is a function of magnetic field ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
Magnetic Flux Quantum
The magnetic flux, represented by the symbol , threading some contour or loop is defined as the magnetic field multiplied by the loop area , i.e. . Both and can be arbitrary, meaning that the flux can be as well but increments of flux can be quantized. The wave function can be multivalued as it happens in the Aharonov–Bohm effect or quantized as in superconductors. The unit of quantization is therefore called magnetic flux quantum. Dirac magnetic flux quantum The first to realize the importance of the flux quantum was Dirac in his publication on monopoles The phenomenon of flux quantization was predicted first by Fritz London then within the Aharonov–Bohm effect and later discovered experimentally in superconductors (see ' below). Superconducting magnetic flux quantum If one deals with a superconducting ring (i.e. a closed loop path in a superconductor) or a hole in a bulk superconductor, the magnetic flux threading such a hole/loop is quantized. The (superco ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Magnetic Flux
In physics, specifically electromagnetism, the magnetic flux through a surface is the surface integral of the normal component of the magnetic field B over that surface. It is usually denoted or . The SI unit of magnetic flux is the weber (Wb; in derived units, volt–seconds or V⋅s), and the CGS unit is the maxwell. Magnetic flux is usually measured with a fluxmeter, which contains measuring coils, and it calculates the magnetic flux from the change of voltage on the coils. Description The magnetic interaction is described in terms of a vector field, where each point in space is associated with a vector that determines what force a moving charge would experience at that point (see Lorentz force). Since a vector field is quite difficult to visualize, introductory physics instruction often uses field lines to visualize this field. The magnetic flux, through some surface, in this simplified picture, is proportional to the number of field lines passing through that ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
 |
Quantum Harmonic Oscillator
The quantum harmonic oscillator is the quantum-mechanical analog of the classical harmonic oscillator. Because an arbitrary smooth potential can usually be approximated as a harmonic potential at the vicinity of a stable equilibrium point, it is one of the most important model systems in quantum mechanics. Furthermore, it is one of the few quantum-mechanical systems for which an exact, analytical solution is known. One-dimensional harmonic oscillator Hamiltonian and energy eigenstates The Hamiltonian of the particle is: \hat H = \frac + \frac k ^2 = \frac + \frac m \omega^2 ^2 \, , where is the particle's mass, is the force constant, \omega = \sqrt is the angular frequency of the oscillator, \hat is the position operator (given by in the coordinate basis), and \hat is the momentum operator (given by \hat p = -i \hbar \, \partial / \partial x in the coordinate basis). The first term in the Hamiltonian represents the kinetic energy of the particle, and the second ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
Gauge Fixing
In the physics of gauge theories, gauge fixing (also called choosing a gauge) denotes a mathematical procedure for coping with redundant degrees of freedom in field variables. By definition, a gauge theory represents each physically distinct configuration of the system as an equivalence class of detailed local field configurations. Any two detailed configurations in the same equivalence class are related by a certain transformation, equivalent to a shear along unphysical axes in configuration space. Most of the quantitative physical predictions of a gauge theory can only be obtained under a coherent prescription for suppressing or ignoring these unphysical degrees of freedom. Although the unphysical axes in the space of detailed configurations are a fundamental property of the physical model, there is no special set of directions "perpendicular" to them. Hence there is an enormous amount of freedom involved in taking a "cross section" representing each physical configuration ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |