|
Critical Point (thermodynamics)
In thermodynamics, a critical point (or critical state) is the end point of a phase Equilibrium (thermodynamics), equilibrium curve. One example is the liquid–vapor critical point, the end point of the pressure–temperature curve that designates conditions under which a liquid and its vapor can coexist. At higher temperatures, the gas comes into a supercritical fluid, supercritical phase, and so cannot be liquefied by pressure alone. At the critical point, defined by a ''critical temperature'' ''T''c and a ''critical pressure'' ''p''c, phase (matter), phase boundaries vanish. Other examples include the Upper critical solution temperature, liquid–liquid critical points in mixtures, and the ferromagnet–paramagnet transition (Curie temperature) in the absence of an external magnetic field. Liquid–vapor critical point Overview For simplicity and clarity, the generic notion of ''critical point'' is best introduced by discussing a specific example, the vapor–liquid cr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
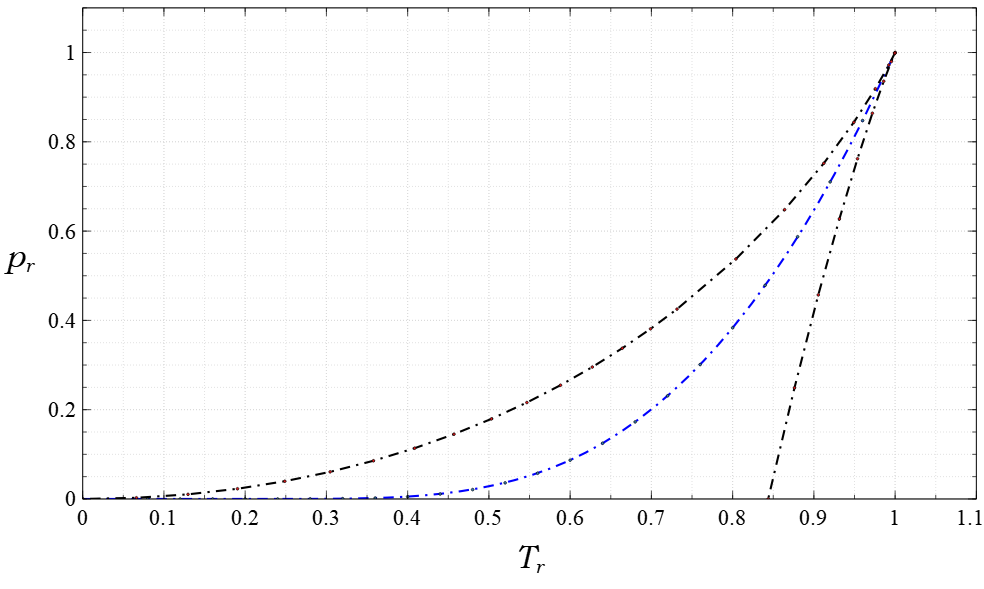
Theorem Of Corresponding States
According to van der Waals, the theorem of corresponding states (or principle/law of corresponding states) indicates that all fluids, when compared at the same reduced temperature and reduced pressure, have approximately the same compressibility factor and all deviate from ideal gas behavior to about the same degree. Material constants that vary for each type of material are eliminated, in a recast reduced form of a constitutive equation. The reduced variables are defined in terms of critical variables. The principle originated with the work of Johannes Diderik van der Waals in about 1873 when he used the critical temperature and critical pressure to derive a universal property of all fluids that follow the van der Waals equation of state. It predicts a value of 3/8 = 0.375 that is found to be an overestimate when compared to real gases. Edward A. Guggenheim used the phrase "Principle of Corresponding States" in an oft-cited paper to describe the phenomenon where different sys ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stationary Point
In mathematics, particularly in calculus, a stationary point of a differentiable function of one variable is a point on the graph of a function, graph of the function where the function's derivative is zero. Informally, it is a point where the function "stops" increasing or decreasing (hence the name). For a differentiable function of several real variables, a stationary point is a point on the surface (mathematics), surface of the graph where all its partial derivatives are zero (equivalently, the gradient has zero vector norm, norm). The notion of stationary points of a real-valued function is generalized as ''Critical point (mathematics), critical points'' for complex-valued functions. Stationary points are easy to visualize on the graph of a function of one variable: they correspond to the points on the graph where the tangent is horizontal (i.e., Parallel (geometry), parallel to the Abscissa, -axis). For a function of two variables, they correspond to the points on the gr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Scaling Law
In statistics, a power law is a functional relationship between two quantities, where a relative change in one quantity results in a relative change in the other quantity proportional to the change raised to a constant exponent: one quantity varies as a power of another. The change is independent of the initial size of those quantities. For instance, the area of a square has a power law relationship with the length of its side, since if the length is doubled, the area is multiplied by 2, while if the length is tripled, the area is multiplied by 3, and so on. Empirical examples The distributions of a wide variety of physical, biological, and human-made phenomena approximately follow a power law over a wide range of magnitudes: these include the sizes of craters on the moon and of solar flares, cloud sizes, the foraging pattern of various species, the sizes of activity patterns of neuronal populations, the frequencies of words in most languages, frequencies of family names, the s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mean-field Theory
In physics and probability theory, Mean-field theory (MFT) or Self-consistent field theory studies the behavior of high-dimensional random (stochastic) models by studying a simpler model that approximates the original by averaging over Degrees of freedom (statistics), degrees of freedom (the number of values in the final calculation of a statistic that are free to vary). Such models consider many individual components that interact with each other. The main idea of MFT is to replace all fundamental interaction, interactions to any one body with an average or effective interaction, sometimes called a ''molecular field''. This reduces any many-body problem into an effective one-body problem. The ease of solving MFT problems means that some insight into the behavior of the system can be obtained at a lower computational cost. MFT has since been applied to a wide range of fields outside of physics, including statistical inference, graphical models, neuroscience, artificial intelligenc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Van Der Waals Equation
The van der Waals equation is a mathematical formula that describes the behavior of real gases. It is an equation of state that relates the pressure, volume, Avogadro's law, number of molecules, and temperature in a fluid. The equation modifies the ideal gas law in two ways: first, it considers particles to have a finite diameter (whereas an ideal gas consists of point particles); second, its particles interact with each other (unlike an ideal gas, whose particles move as though alone in the volume). The equation is named after Dutch physicist Johannes Diderik van der Waals, who first derived it in 1873 as part of his doctoral thesis. Van der Waals based the equation on the idea that fluids are composed of discrete particles, which few scientists believed existed. However, the equation accurately predicted the behavior of a fluid around its Critical point (thermodynamics), critical point, which had been discovered a few years earlier. Its qualitative and quantitative agreement w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thomas Andrews (scientist)
Thomas Andrews FRS FRSE (19 December 181326 November 1885) was an Irish chemist and physicist who did important work on phase transitions between gases and liquids. He was a longtime professor of chemistry at Queen's University of Belfast. Life Andrews was born in Belfast, Ireland, where his father was a linen merchant. He attended the Belfast Academy and the Royal Belfast Academical Institution, where at the latter of which he studied mathematics under James Thomson. In 1828 he went to the University of Glasgow to study chemistry under Professor Thomas Thomson, then studied at Trinity College, Dublin, where he gained distinction in classics as well as in science. Finally, at University of Edinburgh in 1835, he was awarded a doctorate in medicine. Andrews began a successful medical practice in his native Belfast in 1835, also giving instruction in chemistry at the Academical Institution. In 1845 he was appointed vice-president of the newly established Queen's University ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dmitri Mendeleev
Dmitri Ivanovich Mendeleev ( ; ) was a Russian chemist known for formulating the periodic law and creating a version of the periodic table of elements. He used the periodic law not only to correct the then-accepted properties of some known elements, such as the valence and atomic weight of uranium, but also to predict the properties of three elements that were yet to be discovered (germanium, gallium and scandium). Early life Mendeleev was born in the village of Verkhnie Aremzyani, near Tobolsk in Siberia, to Ivan Pavlovich Mendeleev (1783–1847) and Maria Dmitrievna Mendeleeva (née Kornilieva) (1793–1850).''Maria Mendeleeva (1951)''. D. I. Mendeleev's Archive: Autobiographical Writings. Collection of Documents. Volume 1 /Biographical notes about D. I. Mendeleev (written by me – D. Mendeleev), p. 13 – Leningrad: D. I. Mendeleev's Museum-Archive, 207 pages (in Russian) Ivan worked as a school principal and a teacher of fine arts, politics and philosophy at the Tambov an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Charles Cagniard De La Tour
Baron Charles Cagniard de la Tour (31 March 1777 – 5 July 1859) was a French engineer and physicist. Charles Cagniard was born in Paris, and after attending the École Polytechnique became one of the ''ingénieurs géographiques''. He examined the mechanism of voice-production, invented a blowing machine and contributed to acoustics by inventing an improved siren. He also studied yeast. In 1822, he discovered the critical point (thermodynamics), critical point of a substance in his gun barrel experiments. He sealed a flint ball in a sealed gun barrel filled with fluids at various temperatures, and rotated it to hear the splashing sound as it hit the liquid surface. He observed that above a certain temperature, there is no splashing sound. Above this temperature, the densities of the liquid and gas phases become equal and the distinction between them disappears, resulting in a single supercritical fluid phase (matter), phase. After this discovery, he performed quantitative measure ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Critical Carbon Dioxide
Supercritical carbon dioxide (s) is a fluid state of carbon dioxide where it is held at or above its critical temperature and critical pressure. Carbon dioxide usually behaves as a gas in air at standard temperature and pressure (STP), or as a solid called dry ice when cooled and/or pressurised sufficiently. If the temperature and pressure are both increased from STP to be at or above the critical point for carbon dioxide, it can adopt properties midway between a gas and a liquid. More specifically, it behaves as a supercritical fluid above its critical temperature () and critical pressure (), expanding to fill its container like a gas but with a density like that of a liquid. Supercritical is becoming an important commercial and industrial solvent due to its role in chemical extraction, in addition to its relatively low toxicity and environmental impact. The relatively low temperature of the process and the stability of also allows compounds to be extracted with little dam ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Benjamin Widom
Benjamin Widom (October 13, 1927 – January 23, 2025) was an American physical chemist. He was the Goldwin Smith Professor of Chemistry at Cornell University. His research interests included physical chemistry and statistical mechanics. In 1998, Widom was awarded the Boltzmann Medal "for his illuminating studies of the statistical mechanics of fluids and fluid mixtures and their interfacial properties, especially his clear and general formulation of scaling hypotheses for the equation of state and surface tensions of fluids near critical points." Widom's professional papers are archived at Cornell University. Academic background Widom was born in Newark, New Jersey. His younger brother was mathematician Harold Widom. He graduated from New York City's Stuyvesant High School in 1945, and received his BA from Columbia University in 1949, followed by his PhD from Cornell in 1953. He became an instructor of chemistry at Cornell in 1954, was appointed assistant professor in 1955 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Michael Fisher
Michael Ellis Fisher (3 September 1931 – 26 November 2021) was an English physicist, as well as chemist and mathematician, known for his many seminal contributions to statistical physics, including but not restricted to the theory of phase transitions and critical phenomena. He was the Horace White Professor of Chemistry, Physics, and Mathematics at Cornell University. Later he moved to the University of Maryland College of Computer, Mathematical, and Natural Sciences, where he was University System of Maryland Regents Professor, a Distinguished University Professor and Distinguished Scholar-Teacher. Academic background Michael E. Fisher received his BSc from King's College London in 1951, where he also earned a PhD in physics in 1957, studying analogue computing under Donald MacCrimmon MacKay. He was appointed to the faculty as a lecturer the following year, becoming a full professor in 1965. In 1966 he moved to Cornell University where he became professor of chemist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |