Butler–Volmer Equation

In electrochemistry, the Butler–Volmer equation (named after John Alfred Valentine Butler and Max Volmer), also known as Erdey-Grúz–Volmer equation, is one of the most fundamental relationships in electrochemical kinetics. It describes how the electrical current through an electrode depends on the voltage difference between the electrode and the bulk electrolyte for a simple, unimolecular redox reaction, considering that both a cathodic and an anodic reaction occur on the same electrode:

The Butler–Volmer equation

The Butler–Volmer equation is:

:$j = j_0 \cdot \left\$

or in a more compact form:

:$j= j_0 \cdot \left\$

where:
* $j$: electrode current density, A/m² (defined as j ''= I/S'')
*$j_0$: exchange current density, A/m²
* $E$: electrode potential, V
* $E_$: equilibrium potential, V
* $T$: absolute temperature, K
* $z$: number of electrons involved in the electrode reaction
* $F$: Faraday constant
* $R$: universal gas constant
*$\alpha_$: so-called cathodic charge transfer coefficient, dimensionless
*$\alpha_$: so-called anodic charge transfer coefficient, dimensionless
* $\eta$: activation overpotential (defined as $\eta = E - E_$).
The right hand figure shows plots valid for $\alpha_ = 1 - \alpha_$.

The limiting cases

There are two limiting cases of the Butler–Volmer equation:

* the low overpotential region (called "polarization resistance", i.e., when E ≈ E_eq), where the Butler–Volmer equation simplifies to:
:$j = j_0\frac (E-E_)$;

* the high overpotential region, where the Butler–Volmer equation simplifies to the Tafel equation. When $(E-E_)>>0$, the first term dominates, and when $(E-E_)<<0$, the second term dominates.
:$E-E_ = a_ - b_ \log j$ for a cathodic reaction, when E << E_eq, or
:$E-E_ = a_ + b_ \log j$ for an anodic reaction, when E >> E_eq

where $a$ and $b$ are constants (for a given reaction and temperature) and are called the Tafel equation constants. The theoretical values of the Tafel equation constants are different for the cathodic and anodic processes. However, the Tafel slope $b$ can be defined as:
:$b = \left ( \frac \right)_$
where $I_$ is the faradaic current, expressed as $I_ = I_ + I_$, being $I_$ and $I_$ the cathodic and anodic partial currents, respectively.

The extended Butler–Volmer equation

The more general form of the Butler–Volmer equation, applicable to the mass transfer-influenced conditions, can be written as:

:$j = j_0 \left\$

where:
* j is the current density, A/m²,
* c_o and c_r refer to the concentration of the species to be oxidized and to be reduced, respectively,
* c(0,t) is the time-dependent concentration at the distance zero from the surface of the electrode.

The above form simplifies to the conventional one (shown at the top of the article) when the concentration of the electroactive species at the surface is equal to that in the bulk.

There are two rates which determine the current-voltage relationship for an electrode. First is the rate of the chemical reaction at the electrode, which consumes reactants and produces products. This is known as the ''charge transfer'' rate. The second is the rate at which reactants are provided, and products removed, from the electrode region by various processes including diffusion, migration, and convection. The latter is known as the '' mass-transfer'' rate
. These two rates determine the concentrations of the reactants and products at the electrode, which are in turn determined by them. The slowest of these rates will determine the overall rate of the process.

The simple Butler–Volmer equation assumes that the concentrations at the electrode are practically equal to the concentrations in the bulk electrolyte, allowing the current to be expressed as a function of potential only. In other words, it assumes that the mass transfer rate is much greater than the reaction rate, and that the reaction is dominated by the slower chemical reaction rate. Despite this limitation, the utility of the Butler–Volmer equation in electrochemistry is wide, and it is often considered to be "central in the phenomenological electrode kinetics".J. O'M. Bockris, A.K.N.Reddy, and M. Gamboa-Aldeco, "Modern Electrochemistry 2A. Fundamentals of Electrodics.", Second Edition, Kluwer Academic/Plenum Publishers, p.1083, 2000.

The extended Butler–Volmer equation does not make this assumption, but rather takes the concentrations at the electrode as given, yielding a relationship in which the current is expressed as a function not only of potential, but of the given concentrations as well. The mass-transfer rate may be relatively small, but its only effect on the chemical reaction is through the altered (given) concentrations. In effect, the concentrations are a function of the potential as well. A full treatment, which yields the current as a function of potential only, will be expressed by the extended Butler–Volmer equation, but will require explicit inclusion of mass transfer effects in order to express the concentrations as functions of the potential.

Derivation

General expression

The following derivation of the extended Butler–Volmer equation is adapted from that of Bard and Faulkner and Newman and Thomas-Alyea. For a simple unimolecular, one-step reaction of the form:

:O+ne⁻ → R

The forward and backward reaction rates (''v_f'' and ''v_b'') and, from Faraday's laws of electrolysis, the associated electrical current densities (''j''), may be written as:

:$v_f=k_f c_o = j_f/n F$
:$v_b=k_b c_r = j_b/n F$

where ''k_f'' and ''k_b'' are the reaction rate constants, with units of frequency (1/time) and ''c_o'' and ''c_r'' are the surface concentrations (mol/area) of the oxidized and reduced molecules, respectively (written as ''c_o(0,t)'' and ''c_r(0,t)'' in the previous section). The net rate of reaction ''v'' and net current density ''j'' are then:

:$v=v_b-v_f = \frac=\frac$

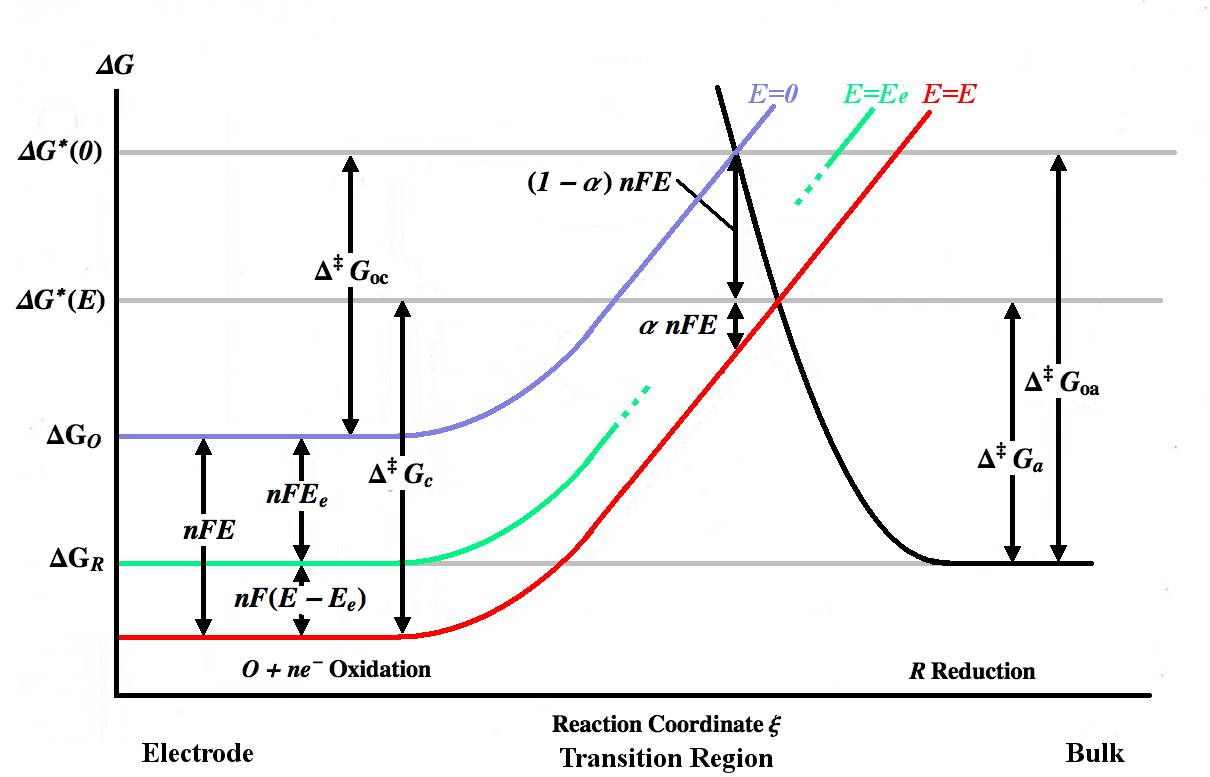
The figure above plots various Gibbs energy curves as a function of the reaction coordinate ξ. The reaction coordinate is roughly a measure of distance, with the body of the electrode being on the left, the bulk solution being on the right. The blue energy curve shows the increase in Gibbs energy for an oxidized molecule as it moves closer to the surface of the electrode when no potential is applied. The black energy curve shows the increase in Gibbs energy as a reduced molecule moves closer to the electrode. The two energy curves intersect at $\Delta G^*(0)$. Applying a potential ''E'' to the electrode will move the energy curve downward (to the red curve) by ''nFE'' and the intersection point will move to $\Delta G^*(E)$. $\Delta^\ddagger G_c$ and $\Delta^\ddagger G_a$ are the activation energies (energy barriers) to be overcome by the oxidized and reduced species respectively for a general ''E'', while $\Delta^\ddagger G_$ and $\Delta^\ddagger G_$ are the activation energies for ''E=0''.

Assume that the rate constants are well approximated by an Arrhenius equation,

:k_f=A_f \exp \Delta^\ddagger G_c/RT/math>
:k_b=A_b \exp \Delta^\ddagger G_a/RT/math>

where the ''A_f'' and ''A_b'' are constants such that ''A_f c_o = A_b c_r'' is the "correctly oriented" ''O-R'' collision frequency, and the exponential term (Boltzmann factor) is the fraction of those collisions with sufficient energy to overcome the barrier and react.

Assuming that the energy curves are practically linear in the transition region, they may be represented there by:

:

The charge transfer coefficient for this simple case is equivalent to the symmetry factor, and can be expressed in terms of the slopes of the energy curves:

:$\alpha=\frac$

It follows that:

:$\Delta^\ddagger G_c = \Delta^\ddagger G_+\alpha nFE$
:$\Delta^\ddagger G_a = \Delta^\ddagger G_-(1-\alpha) nFE$

For conciseness, define:

:$f_\alpha=\alpha nF/RT$
:$f_\beta=(1-\alpha) nF/RT$
:$f=f_\alpha+f_\beta = nF/RT$

The rate constants can now be expressed as:

:$k_f=k_e^$
:$k_b=k_e^$

where the rate constants at zero potential are:

:$k_ = A_f e^$
:$k_ = A_b e^$

The current density ''j'' as a function of applied potential ''E'' may now be written:

:$j = nF(c_r k_ e^-c_o k_ e^)$

Expression in terms of the equilibrium potential

At a certain voltage ''E_e'', equilibrium will attain and the forward and backward rates (''v_f'' and ''v_b'') will be equal. This is represented by the green curve in the above figure. The equilibrium rate constants will be written as ''k_fe'' and ''k_be'', and the equilibrium concentrations will be written ''c_oe'' and ''c_re''. The equilibrium currents (''j_ce'' and ''j_ae'') will be equal and are written as ''j_o'', which is known as the '' exchange current density''.

:$v_=k_ c_ = j_o/nF$
:$v_=k_ c_ = j_o/nF$

Note that the net current density at equilibrium will be zero. The equilibrium rate constants are then:

:$k_ = k_e^$
:$k_ = k_e^$

Solving the above for ''k_fo'' and ''k_bo'' in terms of the equilibrium concentrations ''c_oe'' and ''c_re'' and the exchange current density ''j_o'', the current density ''j'' as a function of applied potential ''E'' may now be written:

:$j=j_o\left(\frace^-\frace^\right)$

Assuming that equilibrium holds in the bulk solution, with concentrations $c_o^*$ and $c_r^*$, it follows that $c_=c_o^*$ and $c_=c_r^*$, and the above expression for the current density ''j'' is then the Butler–Volmer equation. Note that ''E-E_e'' is also known as η, the activation overpotential.

Expression in terms of the formal potential

For the simple reaction, the change in Gibbs energy is:

:$\Delta G = \Delta G_o-\Delta G_r = (\Delta G_o^o-\Delta G_r^o) + RT\ln\left(\frac\right)$

where ''a_oe'' and ''a_re'' are the activities at equilibrium. The activities ''a'' are related to the concentrations ''c'' by ''a=γc'' where γ is the activity coefficient. The equilibrium potential is given by the Nernst equation:

:$E_e=-\frac = E^o + \frac \ln\left(\frac\right)$

where $E^o$ is the standard potential

:$E^o=-(\Delta G_o^o-\Delta G_r^o)/nF$

Defining the ''formal potential'':

:$E^=E^o+\frac\ln\left(\frac\right)$

the equilibrium potential is then:

:$E_e = E^+\frac \ln\left(\frac\right)$

Substituting this equilibrium potential into the Butler–Volmer equation yields:

:$j=\frac\left(c_r e^-c_o e^\right)$

which may also be written in terms of the ''standard rate constant'' ''k^o'' as:

:$j=nFk^o\left(c_r e^-c_o e^\right)$

The standard rate constant is an important descriptor of electrode behavior, independent of concentrations. It is a measure of the rate at which the system will approach equilibrium. In the limit as $k^0\rightarrow 0$, the electrode becomes an ideal polarizable electrode and will behave electrically as an open circuit (neglecting capacitance). For nearly ideal electrodes with small ''k^o'', large changes in the overpotential are required to generate a significant current. In the limit as $k^0\rightarrow \infty$, the electrode becomes an ideal non-polarizable electrode and will behave as an electrical short. For a nearly ideal electrodes with large ''k^o'', small changes in the overpotential will generate large changes in current.

See also

* Advanced Simulation Library
* Nernst equation
* Goldman equation
* Tafel equation

Notes

References

External links

*

{{DEFAULTSORT:Butler-Volmer equation
Chemical kinetics
Electrochemical equations
Physical chemistry