Branched Pathways

Branched pathways, also known as branch points (not to be confused with the mathematical branch point), are a common pattern found in metabolism. This is where an intermediate species is chemically made or transformed by multiple enzymatic processes. linear pathways only have one enzymatic reaction producing a species and one enzymatic reaction consuming the species.

Branched pathways are present in numerous metabolic reactions, including glycolysis, the synthesis of lysine, glutamine, and penicillin, and in the production of the aromatic amino acids.

In general, a single branch may have $b$ producing branches and $d$ consuming branches. If the intermediate at the branch point is given by $s_i$, then the rate of change of $s_i$ is given by:

: $\sum_^b v_i-\sum_^d v_j=\frac$

At steady-state when $ds_i/dt = 0$ the consumption and production rates must be equal:

: $\sum_^b v_i=\sum_^d v_j$

Biochemical pathways can be investigated by computer simulation or by looking at the sensitivities, i.e. control coefficients for flux and species concentrations using metabolic control analysis.

Elementary properties

A simple branched pathway has one key property related to the conservation of mass. In general, the rate of change of the branch species based on the above figure is given by:

: $\frac = v_1 - (v_2 + v_3)$

At steady-state the rate of change of $S_1$ is zero. This gives rise to a steady-state constraint among the branch reaction rates:

: $v_1 = v_2 + v_3$

Such constraints are key to computational methods such as flux balance analysis.

Control properties of a branch pathway

Branched pathways have unique control properties compared to simple linear chain or cyclic pathways. These properties can be investigated using metabolic control analysis. The fluxes can be controlled by enzyme concentrations $e_1$, $e_2$, and $e_3$ respectively, described by the corresponding flux control coefficients. To do this the flux control coefficients with respect to one of the branch fluxes can be derived. The derivation is shown in a subsequent section. The flux control coefficient with respect to the upper branch flux, $J_2$ are given by:

: $C^_ = \frac$

: $C^_ = \frac$

: $C^_ = \frac$

where $\alpha$ is the fraction of flux going through the upper arm, $J_2$, and $1-\alpha$ the fraction going through the lower arm, $J_3$. $\varepsilon_1, \varepsilon_2,$ and $\varepsilon_3$ are the elasticities for $s_1$ with respect to $v_1, v_2,$ and $v_3$ respectively.

For the following analysis, the flux $J_2$ will be the observed variable in response to changes in enzyme concentrations.

There are two possible extremes to consider, either most of the flux goes through the upper branch $J_2$ or most of the flux goes through the lower branch, $J_3$. The former, depicted in panel a), is the least interesting as it converts the branch in to a simple linear pathway. Of more interest is when most of the flux goes through $J_3$

If most of the flux goes through $J_3$, then $\alpha \rightarrow 0$ and $1 - \alpha \rightarrow 1$ (condition (b) in the figure), the flux control coefficients for $J_2$ with respect to $e_2$ and $e_3$ can be written:

: $C^_ \rightarrow 1$

: $C^_ \rightarrow \frac$

That is, $e_2$ acquires proportional influence over its own flux, $J_2$. Since $J_2$ only carries a very small amount of flux, any changes in $e_2$ will have little effect on $S$. Hence the flux through $e_2$ is almost entirely governed by the activity of $e_2$. Because of the flux summation theorem and the fact that $C^_ = 1$, it means that the remaining two coefficients must be equal and opposite in value. Since $C^_$ is positive, $C^_$ must be negative. This also means that in this situation, there can be more than one Rate-limiting step (biochemistry) in a pathway.

Unlike a linear pathway, values for $C^_$and $C^_$ are not bounded between zero and one. Depending on the values of the elasticities, it is possible for the control coefficients in a branched system to greatly exceed one. This has been termed the branchpoint effect by some in the literature.

Example

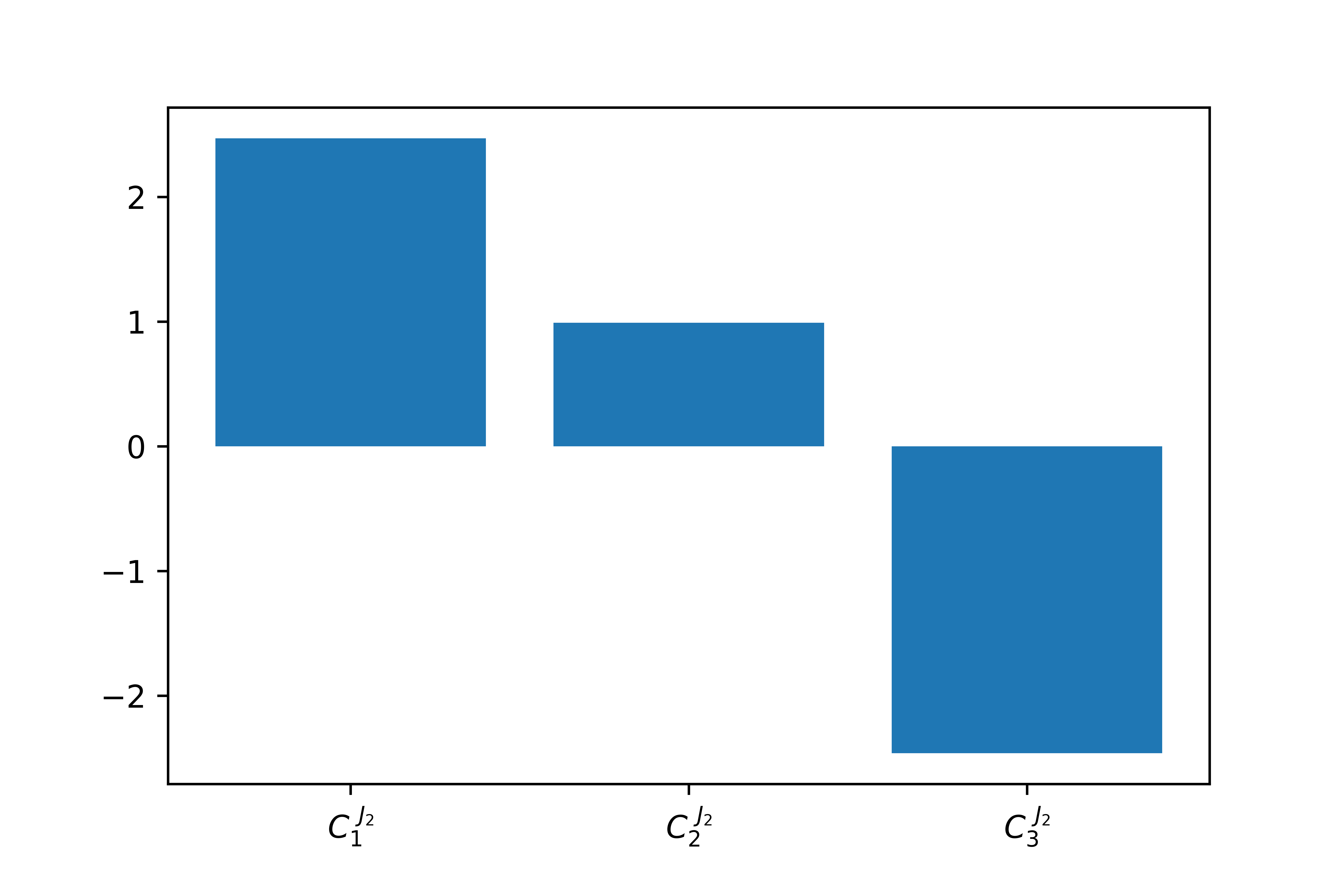
The following branch pathway model (in antimony format) illustrates the case $J_1$ and $J_3$ have very high flux control and step J2 has proportional control.
J1: $Xo -> S1; e1*k1*Xo
J2: S1 ->; e2*k3*S1/(Km1 + S1)
J3: S1 ->; e3*k4*S1/(Km2 + S1)

k1 = 2.5;
k3 = 5.9; k4 = 20.75
Km1 = 4; Km2 = 0.02
Xo =5;
e1 = 1; e2 = 1; e3 = 1

A simulation of this model yields the following values for the flux control coefficients with respect to flux $J_2$

Branch point theorems

In a linear pathway, only two sets of theorems exist, the summation and connectivity theorems. Branched pathways have an additional set of branch centric summation theorems. When combined with the connectivity theorems and the summation theorem, it is possible to derive the control equations shown in the previous section. The deviation of the branch point theorems is as follows.

# Define the fractional flux through $J_2$ and $J_3$ as $\alpha = J_2/J_1$ and $1 - \alpha = J_3/J_1$ respectively.
# Increase $e_2$ by $\delta e_2$. This will decrease $S_1$ and increase $J_1$ through relief of product inhibition.
# Make a compensatory change in $J_1$ by decreasing $e_1$ such that $S_1$ is restored to its original concentration (hence $\delta S_1 = 0$).
# Since $e_1$ and $S_1$ have not changed, $\delta J_1 = 0$.

Following these assumptions two sets of equations can be derived: the flux branch point theorems and the concentration branch point theorems.

Derivation

From these assumptions, the following system equation can be produced:

: $C^_ \frac + C^_ \frac = \frac = 0$

Because $\delta S_1 = 0$ and, assuming that the flux rates are directly related to the enzyme concentration thus, the elasticities, $\varepsilon^_$, equal one, the local equations are:

: $\frac = \frac$

: $\frac = \frac$

Substituting $\frac$ for $\frac$ in the system equation results in:

: $C^_ \frac + C^_ \frac = 0$

Conservation of mass dictates $\delta J_1 = \delta J_2 + \delta J_3$ since $\delta J_1 = 0$ then $\delta v_2 = - \delta v_3$. Substitution eliminates the $\delta v_3$ term from the system equation:

: $C^_ \frac - C^_ \frac = 0$

Dividing out $\frac$ results in:

: $C^_ - C^_ \frac = 0$

: $v_2$ and $v_3$ can be substituted by the fractional rates giving:

: $C^_ - C^_ \frac = 0$

Rearrangement yields the final form of the first flux branch point theorem:

: $C^_(1-\alpha) - C^_ = 0$

Similar derivations result in two more flux branch point theorems and the three concentration branch point theorems.

Flux branch point theorems

: $C^_ (1-\alpha) - C^_ (\alpha) = 0$

: $C^_ (1-\alpha) + C^_ (\alpha) = 0$

: $C^_ (\alpha) + C^_ = 0$

Concentration branch point theorems

: $C^_ (1-\alpha) + C^_ (\alpha) = 0$

: $C^_ (1-\alpha) + C^_ = 0$

: $C^_ (\alpha) + C^_ = 0$

Following the flux summation theorem and the connectivity theorem the following system of equations can be produced for the simple pathway.

: $C^_ + C^_ + C^_ = 1$

: $C^_ + C^_ + C^_ = 1$

: $C^_ + C^_ + C^_ = 1$

: $C^_ \varepsilon^_s + C^_ \varepsilon^_s + C^_ \varepsilon^_s = 0$

: $C^_ \varepsilon^_s + C^_ \varepsilon^_s + C^_ \varepsilon^_s = 0$

: $C^_ \varepsilon^_s + C^_ \varepsilon^_s + C^_ \varepsilon^_s = 0$

Using these theorems plus flux summation and connectivity theorems values for the concentration and flux control coefficients can be determined using linear algebra.

: $C^_ = \frac$

: $C^_ = \frac$

: $C^_ = \frac$

: $C^_ = \frac$

: $C^_ = \frac$

: $C^_ = \frac{\varepsilon_2 \alpha + \varepsilon_3 (1-\alpha) - \varepsilon_1}$

See also

* Control coefficient (biochemistry)
* Elasticity coefficient
* Metabolic control analysis

References

Metabolic pathways