Bose–Einstein statistics on:
[Wikipedia]
[Google]
[Amazon]
In quantum statistics, Bose–Einstein statistics (B–E statistics) describes one of two possible ways in which a collection of non-interacting 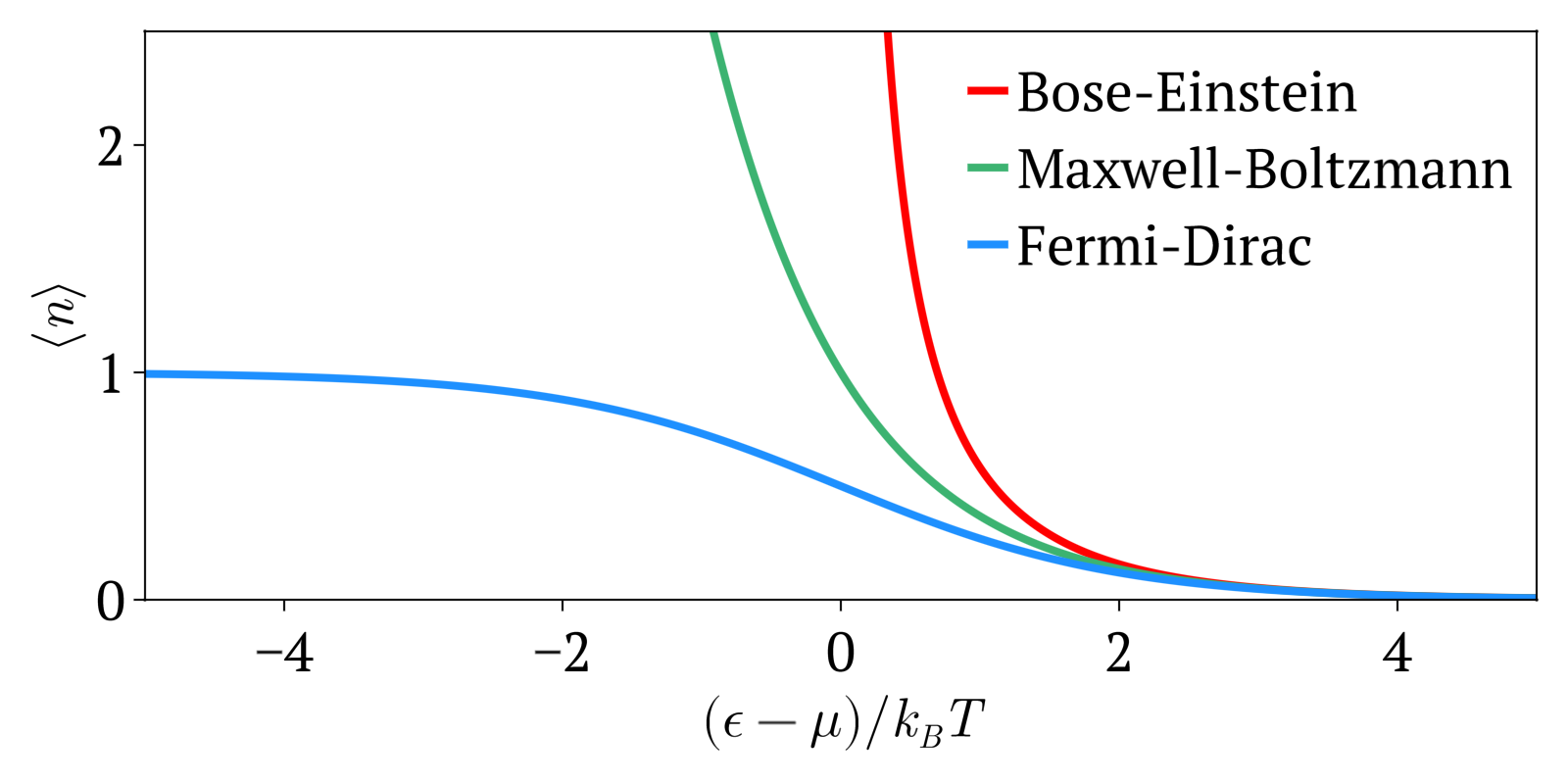
 where is the ''k''-combination of a set with ''m'' elements. The total number of arrangements in an ensemble of bosons is simply the product of the binomial coefficients above over all the energy levels, i.e.
The maximum number of arrangements determining the corresponding occupation number is obtained by maximizing the
where is the ''k''-combination of a set with ''m'' elements. The total number of arrangements in an ensemble of bosons is simply the product of the binomial coefficients above over all the energy levels, i.e.
The maximum number of arrangements determining the corresponding occupation number is obtained by maximizing the
"The ideal Bose–Einstein gas, revisited"
'' OR
The purpose of these notes is to clarify some aspects of the derivation of the Bose–Einstein distribution for beginners. The enumeration of cases (or ways) in the Bose–Einstein distribution can be recast as follows. Consider a game of dice throwing in which there are dice, with each die taking values in the set, for . The constraints of the game are that the value of a die , denoted by , has to be ''greater than or equal to'' the value of die , denoted by , in the previous throw, i.e., . Thus a valid sequence of die throws can be described by an ''n''-tuple , such that . Let denote the set of these valid ''n''-tuples:
Then the quantity ( defined above as the number of ways to distribute particles among the sublevels of an energy level) is the cardinality of , i.e., the number of elements (or valid ''n''-tuples) in . Thus the problem of finding an expression for becomes the problem of counting the elements in .
Example ''n'' = 4, ''g'' = 3:
(there are elements in )
Subset is obtained by fixing all indices to , except for the last index, , which is incremented from to . Subset is obtained by fixing , and incrementing from to . Due to the constraint on the indices in , the index must automatically take values in . The construction of subsets and follows in the same manner.
Each element of can be thought of as a
OR
The purpose of these notes is to clarify some aspects of the derivation of the Bose–Einstein distribution for beginners. The enumeration of cases (or ways) in the Bose–Einstein distribution can be recast as follows. Consider a game of dice throwing in which there are dice, with each die taking values in the set, for . The constraints of the game are that the value of a die , denoted by , has to be ''greater than or equal to'' the value of die , denoted by , in the previous throw, i.e., . Thus a valid sequence of die throws can be described by an ''n''-tuple , such that . Let denote the set of these valid ''n''-tuples:
Then the quantity ( defined above as the number of ways to distribute particles among the sublevels of an energy level) is the cardinality of , i.e., the number of elements (or valid ''n''-tuples) in . Thus the problem of finding an expression for becomes the problem of counting the elements in .
Example ''n'' = 4, ''g'' = 3:
(there are elements in )
Subset is obtained by fixing all indices to , except for the last index, , which is incremented from to . Subset is obtained by fixing , and incrementing from to . Due to the constraint on the indices in , the index must automatically take values in . The construction of subsets and follows in the same manner.
Each element of can be thought of as a
Probabilistic models of information retrieval based on measuring the divergence from randomness
'' ACM TOIS'' 20(4):357–389. the basic notion being that Bose–Einstein statistics may be a useful indicator in cases where a particular term and a particular document have a significant relationship that would not have occurred purely by chance. Source code for implementing this model is available from th
Terrier project
at the University of Glasgow. * The evolution of many complex systems, including the
Bose–Einstein Condensation in Complex Networks
. ''
identical particles
In quantum mechanics, indistinguishable particles (also called identical or indiscernible particles) are particles that cannot be distinguished from one another, even in principle. Species of identical particles include, but are not limited to, ...
may occupy a set of available discrete energy states at thermodynamic equilibrium
Thermodynamic equilibrium is a notion of thermodynamics with axiomatic status referring to an internal state of a single thermodynamic system, or a relation between several thermodynamic systems connected by more or less permeable or impermeable ...
. The aggregation of particles in the same state, which is a characteristic of particles obeying Bose–Einstein statistics, accounts for the cohesive streaming of laser light
A laser is a device that emits light through a process of optical amplification based on the stimulated emission of electromagnetic radiation. The word ''laser'' originated as an acronym for light amplification by stimulated emission of radi ...
and the frictionless creeping of superfluid helium. The theory of this behaviour was developed (1924–25) by Satyendra Nath Bose
Satyendra Nath Bose (; 1 January 1894 – 4 February 1974) was an Indian theoretical physicist and mathematician. He is best known for his work on quantum mechanics in the early 1920s, in developing the foundation for Bose–Einstein statist ...
, who recognized that a collection of identical and indistinguishable particles could be distributed in this way. The idea was later adopted and extended by Albert Einstein
Albert Einstein (14 March 187918 April 1955) was a German-born theoretical physicist who is best known for developing the theory of relativity. Einstein also made important contributions to quantum mechanics. His mass–energy equivalence f ...
in collaboration with Bose.
Bose–Einstein statistics apply only to particles that do not follow the Pauli exclusion principle restrictions. Particles that follow Bose-Einstein statistics are called bosons
In particle physics, a boson ( ) is a subatomic particle whose spin quantum number has an integer value (0, 1, 2, ...). Bosons form one of the two fundamental classes of subatomic particle, the other being fermions, which have half odd-integer ...
, which have integer values of spin. In contrast, particles that follow Fermi-Dirac statistics are called fermion
In particle physics, a fermion is a subatomic particle that follows Fermi–Dirac statistics. Fermions have a half-integer spin (spin 1/2, spin , Spin (physics)#Higher spins, spin , etc.) and obey the Pauli exclusion principle. These particles i ...
s and have half-integer spins.

Bose–Einstein distribution
At low temperatures, bosons behave differently fromfermion
In particle physics, a fermion is a subatomic particle that follows Fermi–Dirac statistics. Fermions have a half-integer spin (spin 1/2, spin , Spin (physics)#Higher spins, spin , etc.) and obey the Pauli exclusion principle. These particles i ...
s (which obey the Fermi–Dirac statistics) in a way that an unlimited number of them can "condense" into the same energy state. This apparently unusual property also gives rise to the special state of matter – the Bose–Einstein condensate
In condensed matter physics, a Bose–Einstein condensate (BEC) is a state of matter that is typically formed when a gas of bosons at very low Density, densities is cooled to temperatures very close to absolute zero#Relation with Bose–Einste ...
. Fermi–Dirac and Bose–Einstein statistics apply when quantum effects
Quantum mechanics is the fundamental physical theory that describes the behavior of matter and of light; its unusual characteristics typically occur at and below the scale of atoms. Reprinted, Addison-Wesley, 1989, It is the foundation of a ...
are important and the particles are " indistinguishable". Quantum effects appear if the concentration of particles satisfies
where is the number of particles, is the volume, and is the quantum concentration, for which the interparticle distance is equal to the thermal de Broglie wavelength, so that the wavefunction
In quantum physics, a wave function (or wavefunction) is a mathematical description of the quantum state of an isolated quantum system. The most common symbols for a wave function are the Greek letters and (lower-case and capital psi (letter) ...
s of the particles are barely overlapping.
Fermi–Dirac statistics applies to fermions (particles that obey the Pauli exclusion principle), and Bose–Einstein statistics applies to bosons
In particle physics, a boson ( ) is a subatomic particle whose spin quantum number has an integer value (0, 1, 2, ...). Bosons form one of the two fundamental classes of subatomic particle, the other being fermions, which have half odd-integer ...
. As the quantum concentration depends on temperature, most systems at high temperatures obey the classical (Maxwell–Boltzmann) limit, unless they also have a very high density, as for a white dwarf
A white dwarf is a Compact star, stellar core remnant composed mostly of electron-degenerate matter. A white dwarf is very density, dense: in an Earth sized volume, it packs a mass that is comparable to the Sun. No nuclear fusion takes place i ...
. Both Fermi–Dirac and Bose–Einstein become Maxwell–Boltzmann statistics
In statistical mechanics, Maxwell–Boltzmann statistics describes the distribution of classical material particles over various energy states in thermal equilibrium. It is applicable when the temperature is high enough or the particle density ...
at high temperature or at low concentration.
Bose–Einstein statistics was introduced for photon
A photon () is an elementary particle that is a quantum of the electromagnetic field, including electromagnetic radiation such as light and radio waves, and the force carrier for the electromagnetic force. Photons are massless particles that can ...
s in 1924 by Bose and generalized to atoms by Einstein
Albert Einstein (14 March 187918 April 1955) was a German-born theoretical physicist who is best known for developing the theory of relativity. Einstein also made important contributions to quantum mechanics. His mass–energy equivalence f ...
in 1924–25.
The expected number of particles in an energy state for Bose–Einstein statistics is:
with and where is the occupation number (the number of particles) in state , is the degeneracy of energy level , is the energy
Energy () is the physical quantity, quantitative physical property, property that is transferred to a physical body, body or to a physical system, recognizable in the performance of Work (thermodynamics), work and in the form of heat and l ...
of the th state, ''μ'' is the chemical potential
In thermodynamics, the chemical potential of a Chemical specie, species is the energy that can be absorbed or released due to a change of the particle number of the given species, e.g. in a chemical reaction or phase transition. The chemical potent ...
(zero for a photon gas In physics, a photon gas is a gas-like collection of photons, which has many of the same properties of a conventional gas like hydrogen or neon – including pressure, temperature, and entropy. The most common example of a photon gas in equilibrium ...
), is the Boltzmann constant
The Boltzmann constant ( or ) is the proportionality factor that relates the average relative thermal energy of particles in a ideal gas, gas with the thermodynamic temperature of the gas. It occurs in the definitions of the kelvin (K) and the ...
, and is the absolute temperature
Thermodynamic temperature, also known as absolute temperature, is a physical quantity which measures temperature starting from absolute zero, the point at which particles have minimal thermal motion.
Thermodynamic temperature is typically expres ...
.
The variance of this distribution is calculated directly from the expression above for the average number.
For comparison, the average number of fermions with energy given by Fermi–Dirac particle-energy distribution has a similar form:
As mentioned above, both the Bose–Einstein distribution and the Fermi–Dirac distribution approaches the Maxwell–Boltzmann distribution
In physics (in particular in statistical mechanics), the Maxwell–Boltzmann distribution, or Maxwell(ian) distribution, is a particular probability distribution named after James Clerk Maxwell and Ludwig Boltzmann.
It was first defined and use ...
in the limit of high temperature and low particle density, without the need for any ad hoc assumptions:
* In the limit of low particle density, , therefore or equivalently . In that case, , which is the result from Maxwell–Boltzmann statistics.
* In the limit of high temperature, the particles are distributed over a large range of energy values, therefore the occupancy on each state (especially the high energy ones with ) is again very small, . This again reduces to Maxwell–Boltzmann statistics.
In addition to reducing to the Maxwell–Boltzmann distribution
In physics (in particular in statistical mechanics), the Maxwell–Boltzmann distribution, or Maxwell(ian) distribution, is a particular probability distribution named after James Clerk Maxwell and Ludwig Boltzmann.
It was first defined and use ...
in the limit of high and low density, Bose–Einstein statistics also reduces to Rayleigh–Jeans law
In physics, the Rayleigh–Jeans law is an approximation to the spectral radiance of electromagnetic radiation as a function of wavelength from a black body at a given temperature through classical arguments. For wavelength ''λ'', it is
B_\l ...
distribution for low energy states with , namely
History
In 1900,Max Planck
Max Karl Ernst Ludwig Planck (; ; 23 April 1858 – 4 October 1947) was a German Theoretical physics, theoretical physicist whose discovery of energy quantum, quanta won him the Nobel Prize in Physics in 1918.
Planck made many substantial con ...
derived the Planck law to explain blackbody radiation. For this purpose, he introduced the concept of quanta of energy.
Władysław Natanson
Władysław Natanson (1864–1937) was a Polish physicist. Natanson was head of Theoretical Physics at Jagiellonian University from 1899 to 1935.
in 1911 concluded that Planck's law requires indistinguishability of "units of energy", although he did not frame this in terms of Einstein's light quanta.
While presenting a lecture at the University of Dhaka
The University of Dhaka (), also known as Dhaka University (DU), is a public university, public research university located in Dhaka, Bangladesh. Established in 1921, it is the oldest active university in the country.
The University of Dhaka w ...
(in what was then British India
The provinces of India, earlier presidencies of British India and still earlier, presidency towns, were the administrative divisions of British governance in South Asia. Collectively, they have been called British India. In one form or another ...
and is now Bangladesh
Bangladesh, officially the People's Republic of Bangladesh, is a country in South Asia. It is the List of countries and dependencies by population, eighth-most populous country in the world and among the List of countries and dependencies by ...
) on the theory of radiation and the ultraviolet catastrophe
The ultraviolet catastrophe, also called the Rayleigh–Jeans catastrophe, was the prediction of late 19th century and early 20th century classical physics that an ideal black body at thermal equilibrium would emit an unbounded quantity of en ...
, Satyendra Nath Bose
Satyendra Nath Bose (; 1 January 1894 – 4 February 1974) was an Indian theoretical physicist and mathematician. He is best known for his work on quantum mechanics in the early 1920s, in developing the foundation for Bose–Einstein statist ...
intended to show his students that the contemporary theory was inadequate, because it predicted results not in accordance with experimental results. During this lecture, Bose committed an error in applying the theory, which unexpectedly gave a prediction that agreed with the experiment. The error was a simple mistake – similar to arguing that flipping two fair coins will produce two heads one-third of the time – that would appear obviously wrong to anyone with a basic understanding of statistics (remarkably, this error resembled the famous blunder by Jean le Rond d'Alembert
Jean-Baptiste le Rond d'Alembert ( ; ; 16 November 1717 – 29 October 1783) was a French mathematician, mechanician, physicist, philosopher, and music theorist. Until 1759 he was, together with Denis Diderot, a co-editor of the ''Encyclopé ...
known from his ''Croix ou Pile'' article). However, the results it predicted agreed with experiment, and Bose realized it might not be a mistake after all. For the first time, he took the position that the Maxwell–Boltzmann distribution would not be true for all microscopic particles at all scales. Thus, he studied the probability of finding particles in various states in phase space, where each state is a little patch having phase volume of ''h''3, and the position and momentum of the particles are not kept particularly separate but are considered as one variable.
Bose adapted this lecture into a short article called "Planck's law and the hypothesis of light quanta" and submitted it to the ''Philosophical Magazine
The ''Philosophical Magazine'' is one of the oldest scientific journals published in English. It was established by Alexander Tilloch in 1798;John Burnett"Tilloch, Alexander (1759–1825)" Dictionary of National Biography#Oxford Dictionary of ...
''. However, the referee's report was negative, and the paper was rejected. Undaunted, he sent the manuscript to Albert Einstein requesting publication in the . Einstein immediately agreed, personally translated the article from English into German (Bose had earlier translated Einstein's article on the general theory of relativity from German to English), and saw to it that it was published. Bose's theory achieved respect when Einstein sent his own paper in support of Bose's to , asking that they be published together. The paper came out in 1924.
The reason Bose produced accurate results was that since photons are indistinguishable from each other, one cannot treat any two photons having equal quantum numbers (e.g., polarization and momentum vector) as being two distinct identifiable photons. Bose originally had a factor of 2 for the possible spin states, but Einstein changed it to polarization. By analogy, if in an alternate universe coins were to behave like photons and other bosons, the probability of producing two heads would indeed be one-third, and so is the probability of getting a head and a tail which equals one-half for the conventional (classical, distinguishable) coins. Bose's "error" leads to what is now called Bose–Einstein statistics.
Bose and Einstein extended the idea to atoms and this led to the prediction of the existence of phenomena which became known as Bose–Einstein condensate, a dense collection of bosons (which are particles with integer spin, named after Bose), which was demonstrated to exist by experiment in 1995.
Derivation
Derivation from the microcanonical ensemble
In themicrocanonical ensemble
In statistical mechanics, the microcanonical ensemble is a statistical ensemble that represents the possible states of a mechanical system whose total energy is exactly specified. The system is assumed to be isolated in the sense that it canno ...
, one considers a system with fixed energy, volume, and number of particles. We take a system composed of identical bosons, of which have energy and are distributed over levels or states with the same energy , i.e. is the degeneracy associated with energy of total energy . Calculation of the number of arrangements of particles distributed among states is a problem of combinatorics
Combinatorics is an area of mathematics primarily concerned with counting, both as a means and as an end to obtaining results, and certain properties of finite structures. It is closely related to many other areas of mathematics and has many ...
. Since particles are indistinguishable in the quantum mechanical context here, the number of ways for arranging particles in boxes (for the th energy level) would be (see image):
 where is the ''k''-combination of a set with ''m'' elements. The total number of arrangements in an ensemble of bosons is simply the product of the binomial coefficients above over all the energy levels, i.e.
The maximum number of arrangements determining the corresponding occupation number is obtained by maximizing the
where is the ''k''-combination of a set with ''m'' elements. The total number of arrangements in an ensemble of bosons is simply the product of the binomial coefficients above over all the energy levels, i.e.
The maximum number of arrangements determining the corresponding occupation number is obtained by maximizing the entropy
Entropy is a scientific concept, most commonly associated with states of disorder, randomness, or uncertainty. The term and the concept are used in diverse fields, from classical thermodynamics, where it was first recognized, to the micros ...
, or equivalently, setting and taking the subsidiary conditions into account (as Lagrange multiplier
In mathematical optimization, the method of Lagrange multipliers is a strategy for finding the local maxima and minima of a function (mathematics), function subject to constraint (mathematics), equation constraints (i.e., subject to the conditio ...
s). The result for , , is the Bose–Einstein distribution.
Derivation from the grand canonical ensemble
The Bose–Einstein distribution, which applies only to a quantum system of non-interacting bosons, is naturally derived from thegrand canonical ensemble
In statistical mechanics, the grand canonical ensemble (also known as the macrocanonical ensemble) is the statistical ensemble that is used to represent the possible states of a mechanical system of particles that are in thermodynamic equilibri ...
without any approximations.
In this ensemble, the system is able to exchange energy and exchange particles with a reservoir (temperature ''T'' and chemical potential ''μ'' fixed by the reservoir).
Due to the non-interacting quality, each available single-particle level (with energy level ''ϵ'') forms a separate thermodynamic system in contact with the reservoir. That is, the number of particles within the overall system ''that occupy a given single particle state'' form a sub-ensemble that is also grand canonical ensemble; hence, it may be analysed through the construction of a grand partition function.
Every single-particle state is of a fixed energy, . As the sub-ensemble associated with a single-particle state varies by the number of particles only, it is clear that the total energy of the sub-ensemble is also directly proportional to the number of particles in the single-particle state; where is the number of particles, the total energy of the sub-ensemble will then be . Beginning with the standard expression for a grand partition function and replacing with , the grand partition function takes the form
This formula applies to fermionic systems as well as bosonic systems. Fermi–Dirac statistics arises when considering the effect of the Pauli exclusion principle: whilst the number of fermions occupying the same single-particle state can only be either 1 or 0, the number of bosons occupying a single particle state may be any integer. Thus, the grand partition function for bosons can be considered a geometric series
In mathematics, a geometric series is a series (mathematics), series summing the terms of an infinite geometric sequence, in which the ratio of consecutive terms is constant. For example, 1/2 + 1/4 + 1/8 + 1/16 + ⋯, the series \tfrac12 + \tfrac1 ...
and may be evaluated as such:
Note that the geometric series is convergent only if , including the case where . This implies that the chemical potential for the Bose gas must be negative, i.e., , whereas the Fermi gas is allowed to take both positive and negative values for the chemical potential.
The average particle number for that single-particle substate is given by
This result applies for each single-particle level and thus forms the Bose–Einstein distribution for the entire state of the system.
The variance
In probability theory and statistics, variance is the expected value of the squared deviation from the mean of a random variable. The standard deviation (SD) is obtained as the square root of the variance. Variance is a measure of dispersion ...
in particle number, , is:
As a result, for highly occupied states the standard deviation
In statistics, the standard deviation is a measure of the amount of variation of the values of a variable about its Expected value, mean. A low standard Deviation (statistics), deviation indicates that the values tend to be close to the mean ( ...
of the particle number of an energy level is very large, slightly larger than the particle number itself: . This large uncertainty is due to the fact that the probability distribution
In probability theory and statistics, a probability distribution is a Function (mathematics), function that gives the probabilities of occurrence of possible events for an Experiment (probability theory), experiment. It is a mathematical descri ...
for the number of bosons in a given energy level is a geometric distribution
In probability theory and statistics, the geometric distribution is either one of two discrete probability distributions:
* The probability distribution of the number X of Bernoulli trials needed to get one success, supported on \mathbb = \;
* T ...
; somewhat counterintuitively, the most probable value for ''N'' is always 0. (In contrast, classical particles have instead a Poisson distribution
In probability theory and statistics, the Poisson distribution () is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time if these events occur with a known const ...
in particle number for a given state, with a much smaller uncertainty of , and with the most-probable ''N'' value being near .)
Derivation in the canonical approach
It is also possible to derive approximate Bose–Einstein statistics in thecanonical ensemble
In statistical mechanics, a canonical ensemble is the statistical ensemble that represents the possible states of a mechanical system in thermal equilibrium with a heat bath at a fixed temperature. The system can exchange energy with the hea ...
. These derivations are lengthy and only yield the above results in the asymptotic limit of a large number of particles. The reason is that the total number of bosons is fixed in the canonical ensemble. The Bose–Einstein distribution in this case can be derived as in most texts by maximization, but the mathematically best derivation is by the Darwin–Fowler method of mean values as emphasized by Dingle. See also Müller-Kirsten.H. J. W. Müller-Kirsten, ''Basics of Statistical Physics'', 2nd ed., World Scientific (2013), . The fluctuations of the ground state in the condensed region are however markedly different in the canonical and grand-canonical ensembles.Ziff R. M.; Kac, M.; Uhlenbeck, G. E. (1977)"The ideal Bose–Einstein gas, revisited"
''
Physics Reports
''Physics Reports'' is a peer-reviewed scientific journal, a review section of '' Physics Letters'' that has been published by Elsevier since 1971. The journal publishes long and deep reviews on all aspects of physics. In average, the length of th ...
'' 32: 169–248.
Suppose we have a number of energy levels, labeled by index , each level having energy and containing a total of particles. Suppose each level contains distinct sublevels, all of which have the same energy, and which are distinguishable. For example, two particles may have different momenta, in which case they are distinguishable from each other, yet they can still have the same energy.
The value of associated with level is called the "degeneracy" of that energy level. Any number of bosons can occupy the same sublevel.
Let be the number of ways of distributing particles among the sublevels of an energy level. There is only one way of distributing particles with one sublevel, therefore . It is easy to see that there are ways of distributing particles in two sublevels which we will write as:
With a little thought (see Notes
Note, notes, or NOTE may refer to:
Music and entertainment
* Musical note, a pitched sound (or a symbol for a sound) in music
* ''Notes'' (album), a 1987 album by Paul Bley and Paul Motian
* ''Notes'', a common (yet unofficial) shortened versi ...
below) it can be seen that the number of ways of distributing particles in three sublevels is
so that
where we have used the following theorem involving binomial coefficient
In mathematics, the binomial coefficients are the positive integers that occur as coefficients in the binomial theorem. Commonly, a binomial coefficient is indexed by a pair of integers and is written \tbinom. It is the coefficient of the t ...
s:
Continuing this process, we can see that is just a binomial coefficient
(See Notes
Note, notes, or NOTE may refer to:
Music and entertainment
* Musical note, a pitched sound (or a symbol for a sound) in music
* ''Notes'' (album), a 1987 album by Paul Bley and Paul Motian
* ''Notes'', a common (yet unofficial) shortened versi ...
below)
For example, the population numbers for two particles in three sublevels are 200, 110, 101, 020, 011, or 002 for a total of six which equals 4!/(2!2!). The number of ways that a set of occupation numbers can be realized is the product of the ways that each individual energy level can be populated:
where the approximation assumes that .
Following the same procedure used in deriving the Maxwell–Boltzmann statistics
In statistical mechanics, Maxwell–Boltzmann statistics describes the distribution of classical material particles over various energy states in thermal equilibrium. It is applicable when the temperature is high enough or the particle density ...
, we wish to find the set of for which ''W'' is maximised, subject to the constraint that there be a fixed total number of particles, and a fixed total energy. The maxima of and occur at the same value of and, since it is easier to accomplish mathematically, we will maximise the latter function instead. We constrain our solution using Lagrange multipliers
In mathematical optimization, the method of Lagrange multipliers is a strategy for finding the local maxima and minima of a function subject to equation constraints (i.e., subject to the condition that one or more equations have to be satisfie ...
forming the function:
Using the approximation and using Stirling's approximation
In mathematics, Stirling's approximation (or Stirling's formula) is an asymptotic approximation for factorials. It is a good approximation, leading to accurate results even for small values of n. It is named after James Stirling, though a related ...
for the factorials gives
where ''K'' is the sum of a number of terms which are not functions of the . Taking the derivative with respect to , and setting the result to zero and solving for , yields the Bose–Einstein population numbers:
By a process similar to that outlined in the Maxwell–Boltzmann statistics
In statistical mechanics, Maxwell–Boltzmann statistics describes the distribution of classical material particles over various energy states in thermal equilibrium. It is applicable when the temperature is high enough or the particle density ...
article, it can be seen that:
which, using Boltzmann's famous relationship becomes a statement of the second law of thermodynamics
The second law of thermodynamics is a physical law based on Universal (metaphysics), universal empirical observation concerning heat and Energy transformation, energy interconversions. A simple statement of the law is that heat always flows spont ...
at constant volume, and it follows that and where ''S'' is the entropy
Entropy is a scientific concept, most commonly associated with states of disorder, randomness, or uncertainty. The term and the concept are used in diverse fields, from classical thermodynamics, where it was first recognized, to the micros ...
, is the chemical potential
In thermodynamics, the chemical potential of a Chemical specie, species is the energy that can be absorbed or released due to a change of the particle number of the given species, e.g. in a chemical reaction or phase transition. The chemical potent ...
, ''k''B is the Boltzmann constant
The Boltzmann constant ( or ) is the proportionality factor that relates the average relative thermal energy of particles in a ideal gas, gas with the thermodynamic temperature of the gas. It occurs in the definitions of the kelvin (K) and the ...
and ''T'' is the temperature
Temperature is a physical quantity that quantitatively expresses the attribute of hotness or coldness. Temperature is measurement, measured with a thermometer. It reflects the average kinetic energy of the vibrating and colliding atoms making ...
, so that finally:
Note that the above formula is sometimes written:
where is the absolute activity, as noted by McQuarrie.See McQuarrie in citations
Also note that when the particle numbers are not conserved, removing the conservation of particle numbers constraint is equivalent to setting and therefore the chemical potential to zero. This will be the case for photons and massive particles in mutual equilibrium and the resulting distribution will be the Planck distribution.
A much simpler way to think of Bose–Einstein distribution function is to consider that n particles are denoted by identical balls and g shells are marked by g-1 line partitions. It is clear that the permutation
In mathematics, a permutation of a set can mean one of two different things:
* an arrangement of its members in a sequence or linear order, or
* the act or process of changing the linear order of an ordered set.
An example of the first mean ...
s of these n balls and g − 1 partitions will give different ways of arranging bosons in different energy levels. Say, for 3 (= ''n'') particles and 3 (= ''g'') shells, therefore , the arrangement might be , ●●, ●, or , , ●●●, or , ●, ●● , etc. Hence the number of distinct permutations of objects which have ''n'' identical items and (''g'' − 1) identical items will be:
See the image for a visual representation of one such distribution of ''n'' particles in ''g'' boxes that can be represented as partitions.  OR
The purpose of these notes is to clarify some aspects of the derivation of the Bose–Einstein distribution for beginners. The enumeration of cases (or ways) in the Bose–Einstein distribution can be recast as follows. Consider a game of dice throwing in which there are dice, with each die taking values in the set, for . The constraints of the game are that the value of a die , denoted by , has to be ''greater than or equal to'' the value of die , denoted by , in the previous throw, i.e., . Thus a valid sequence of die throws can be described by an ''n''-tuple , such that . Let denote the set of these valid ''n''-tuples:
Then the quantity ( defined above as the number of ways to distribute particles among the sublevels of an energy level) is the cardinality of , i.e., the number of elements (or valid ''n''-tuples) in . Thus the problem of finding an expression for becomes the problem of counting the elements in .
Example ''n'' = 4, ''g'' = 3:
(there are elements in )
Subset is obtained by fixing all indices to , except for the last index, , which is incremented from to . Subset is obtained by fixing , and incrementing from to . Due to the constraint on the indices in , the index must automatically take values in . The construction of subsets and follows in the same manner.
Each element of can be thought of as a
OR
The purpose of these notes is to clarify some aspects of the derivation of the Bose–Einstein distribution for beginners. The enumeration of cases (or ways) in the Bose–Einstein distribution can be recast as follows. Consider a game of dice throwing in which there are dice, with each die taking values in the set, for . The constraints of the game are that the value of a die , denoted by , has to be ''greater than or equal to'' the value of die , denoted by , in the previous throw, i.e., . Thus a valid sequence of die throws can be described by an ''n''-tuple , such that . Let denote the set of these valid ''n''-tuples:
Then the quantity ( defined above as the number of ways to distribute particles among the sublevels of an energy level) is the cardinality of , i.e., the number of elements (or valid ''n''-tuples) in . Thus the problem of finding an expression for becomes the problem of counting the elements in .
Example ''n'' = 4, ''g'' = 3:
(there are elements in )
Subset is obtained by fixing all indices to , except for the last index, , which is incremented from to . Subset is obtained by fixing , and incrementing from to . Due to the constraint on the indices in , the index must automatically take values in . The construction of subsets and follows in the same manner.
Each element of can be thought of as a multiset
In mathematics, a multiset (or bag, or mset) is a modification of the concept of a set that, unlike a set, allows for multiple instances for each of its elements. The number of instances given for each element is called the ''multiplicity'' of ...
of cardinality ; the elements of such multiset are taken from the set of cardinality , and the number of such multisets is the multiset coefficient
More generally, each element of is a multiset
In mathematics, a multiset (or bag, or mset) is a modification of the concept of a set that, unlike a set, allows for multiple instances for each of its elements. The number of instances given for each element is called the ''multiplicity'' of ...
of cardinality (number of dice) with elements taken from the set of cardinality (number of possible values of each die), and the number of such multisets, i.e., is the multiset coefficient
which is exactly the same as the formula
In science, a formula is a concise way of expressing information symbolically, as in a mathematical formula or a ''chemical formula''. The informal use of the term ''formula'' in science refers to the general construct of a relationship betwe ...
for , as derived above with the aid of a theorem
In mathematics and formal logic, a theorem is a statement (logic), statement that has been Mathematical proof, proven, or can be proven. The ''proof'' of a theorem is a logical argument that uses the inference rules of a deductive system to esta ...
involving binomial coefficients, namely
To understand the decomposition
or for example, and
let us rearrange the elements of as follows
Clearly, the subset of is the same as the set
By deleting the index (shown in red with double underline) in the subset of , one obtains the set
In other words, there is a one-to-one correspondence between the subset of and the set . We write
Similarly, it is easy to see that
Thus we can write
or more generally,
and since the sets
are non-intersecting, we thus have
with the convention that
Continuing the process, we arrive at the following formula
Using the convention (7)2 above, we obtain the formula
keeping in mind that for and being constants, we have
It can then be verified that (8) and (2) give the same result for , , , etc.
Interdisciplinary applications
Viewed as a pureprobability distribution
In probability theory and statistics, a probability distribution is a Function (mathematics), function that gives the probabilities of occurrence of possible events for an Experiment (probability theory), experiment. It is a mathematical descri ...
, the Bose–Einstein distribution has found application in other fields:
* In recent years, Bose–Einstein statistics has also been used as a method for term weighting in information retrieval
Information retrieval (IR) in computing and information science is the task of identifying and retrieving information system resources that are relevant to an Information needs, information need. The information need can be specified in the form ...
. The method is one of a collection of DFR ("Divergence From Randomness") models,Amati, G.; C. J. Van Rijsbergen (2002).Probabilistic models of information retrieval based on measuring the divergence from randomness
'' ACM TOIS'' 20(4):357–389. the basic notion being that Bose–Einstein statistics may be a useful indicator in cases where a particular term and a particular document have a significant relationship that would not have occurred purely by chance. Source code for implementing this model is available from th
Terrier project
at the University of Glasgow. * The evolution of many complex systems, including the
World Wide Web
The World Wide Web (WWW or simply the Web) is an information system that enables Content (media), content sharing over the Internet through user-friendly ways meant to appeal to users beyond Information technology, IT specialists and hobbyis ...
, business, and citation networks, is encoded in the dynamic web describing the interactions between the system's constituents. Despite their irreversible and nonequilibrium nature these networks follow Bose statistics and can undergo Bose–Einstein condensation. Addressing the dynamical properties of these nonequilibrium systems within the framework of equilibrium quantum gases predicts that the "first-mover-advantage", "fit-get-rich" (FGR) and "winner-takes-all" phenomena observed in competitive systems are thermodynamically distinct phases of the underlying evolving networks. Bianconi, G.; Barabási, A.-L. (2001).Bose–Einstein Condensation in Complex Networks
. ''
Physical Review Letters
''Physical Review Letters'' (''PRL''), established in 1958, is a peer-reviewed, scientific journal that is published 52 times per year by the American Physical Society. The journal is considered one of the most prestigious in the field of physics ...
'' 86: 5632–5635.
See also
*Bose–Einstein correlations
In astronomy, optics and particle physics, the Bose–Einstein correlations refer to correlations between identical bosons (like the photon, the quanta of light).
Description
The interference between two (or more) waves establishes a corre ...
* Bose–Einstein condensate
In condensed matter physics, a Bose–Einstein condensate (BEC) is a state of matter that is typically formed when a gas of bosons at very low Density, densities is cooled to temperatures very close to absolute zero#Relation with Bose–Einste ...
* Bose gas
* Einstein solid
* Higgs boson
The Higgs boson, sometimes called the Higgs particle, is an elementary particle in the Standard Model of particle physics produced by the excited state, quantum excitation of the Higgs field,
one of the field (physics), fields in particl ...
* Parastatistics
In quantum mechanics and statistical mechanics, parastatistics is a hypothetical alternative to the established particle statistics models (Bose–Einstein statistics, Fermi–Dirac statistics and Maxwell–Boltzmann statistics). Other alterna ...
* Planck's law of black body radiation
* Superconductivity
Superconductivity is a set of physical properties observed in superconductors: materials where Electrical resistance and conductance, electrical resistance vanishes and Magnetic field, magnetic fields are expelled from the material. Unlike an ord ...
* Fermi–Dirac statistics
* Maxwell–Boltzmann statistics
In statistical mechanics, Maxwell–Boltzmann statistics describes the distribution of classical material particles over various energy states in thermal equilibrium. It is applicable when the temperature is high enough or the particle density ...
* Kompaneyets equation
Notes
References
* * * * {{DEFAULTSORT:Bose-Einstein statistics Concepts in physics Quantum field theory Albert Einstein Statistical mechanics Satyendra Nath Bose