|
Kompaneyets Equation
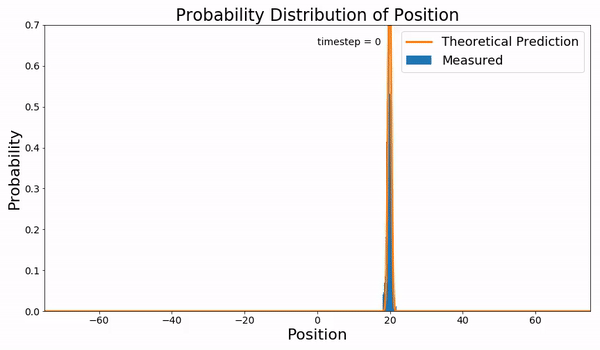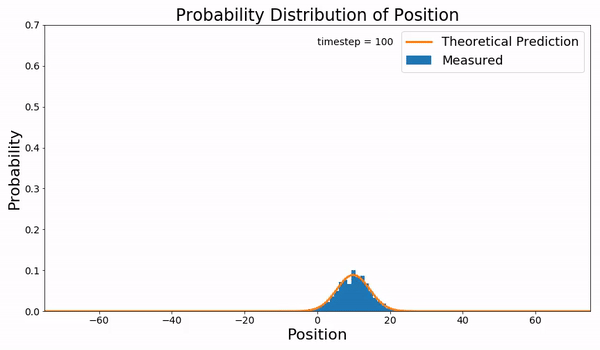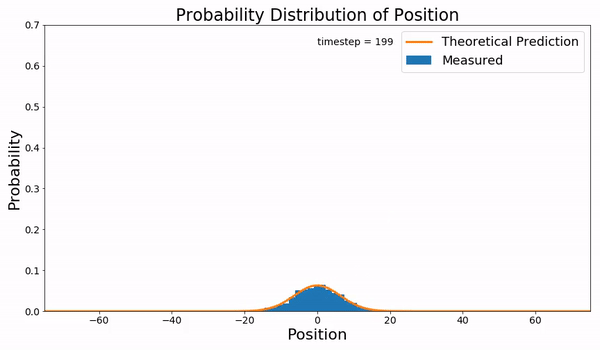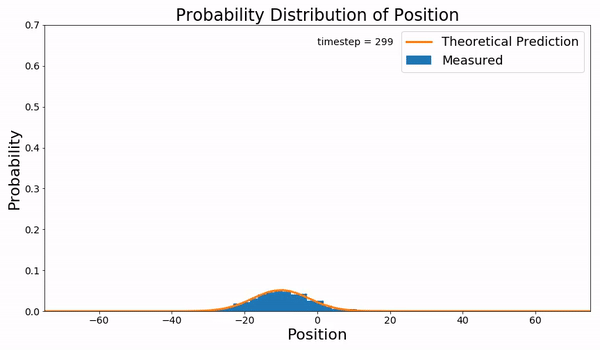
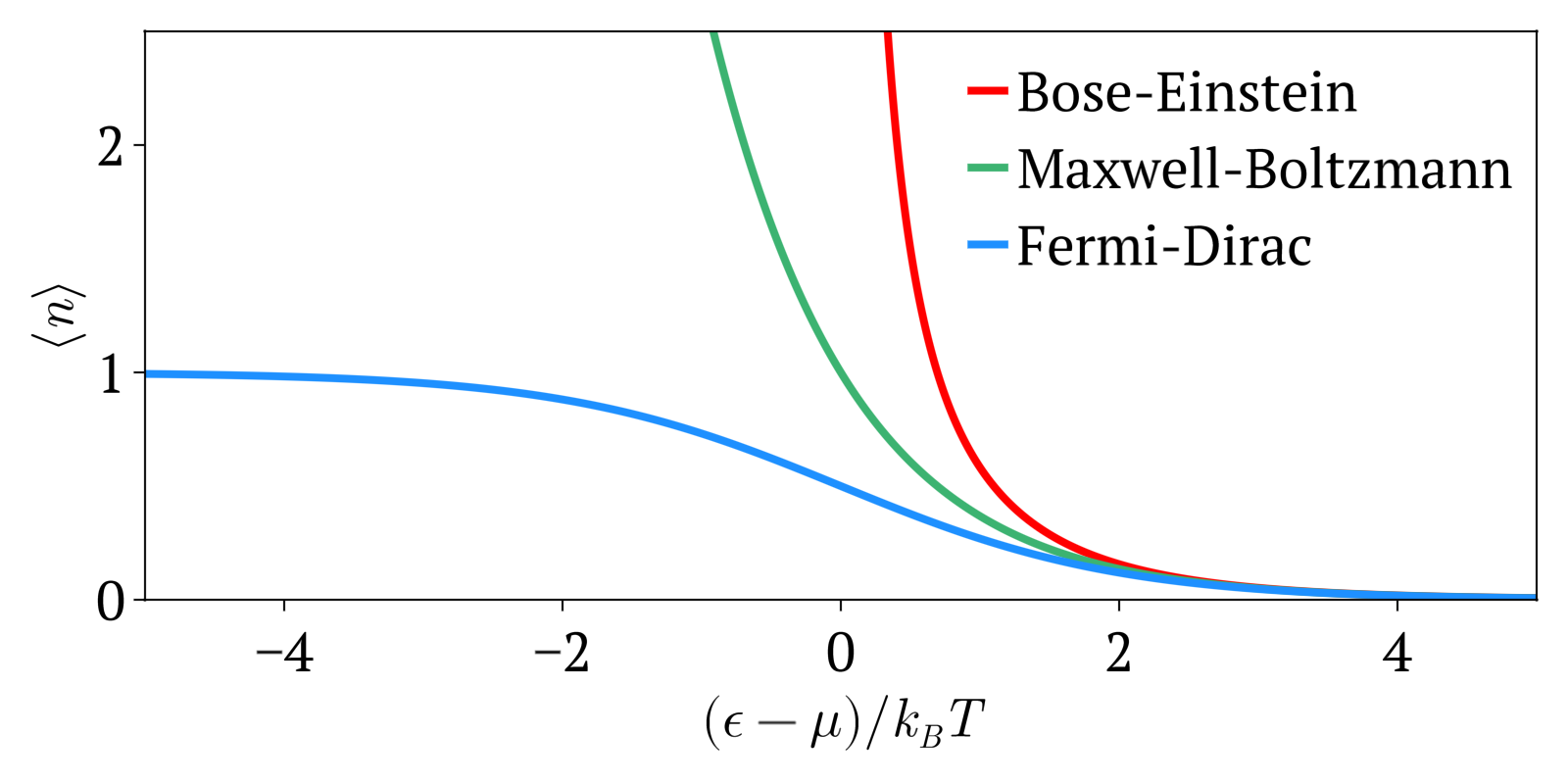
Kompaneyets equation refers to a non-relativistic, Fokker–Planck type, kinetic equation for photon number density with which photons interact with an electron gas via Compton scattering, first derived by Alexander Kompaneyets in 1949 and published in 1957 after declassification. The Kompaneyets equation describes how an initial photon distribution relaxes to the equilibrium Bose–Einstein distribution. Kompaneyets pointed out the radiation field on its own cannot reach the equilibrium distribution since the Maxwells equation are linear but it needs to exchange energy with the electron gas. The Kompaneyets equation has been used as a basis for analysis of the Sunyaev–Zeldovich effect. Mathematical description Consider a non-relativistic electron bath that is at an equilibrium temperature T_e, i.e., k_B T_e\ll m_e c^2, where m_e is the electron mass. Let there be a low-frequency radiation field that satisfies the soft-photon approximation, i.e., \hbar\omega \ll m_ec^2 where \o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fokker–Planck Equation
In statistical mechanics and information theory, the Fokker–Planck equation is a partial differential equation that describes the time evolution of the probability density function of the velocity of a particle under the influence of drag (physics), drag forces and random forces, as in Brownian motion. The equation can be generalized to other observables as well. The Fokker–Planck equation has multiple applications in information theory, graph theory, data science, finance, economics etc. It is named after Adriaan Fokker and Max Planck, who described it in 1914 and 1917. It is also known as the Kolmogorov forward equation, after Andrey Kolmogorov, who independently discovered it in 1931. When applied to particle position distributions, it is better known as the Smoluchowski equation (after Marian Smoluchowski), and in this context it is equivalent to the convection–diffusion equation. When applied to particle position and momentum distributions, it is known as the Klein–Kr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boltzmann Equation
The Boltzmann equation or Boltzmann transport equation (BTE) describes the statistical behaviour of a thermodynamic system not in a state of equilibrium; it was devised by Ludwig Boltzmann in 1872.Encyclopaedia of Physics (2nd Edition), R. G. Lerner, G. L. Trigg, VHC publishers, 1991, ISBN (Verlagsgesellschaft) 3-527-26954-1, ISBN (VHC Inc.) 0-89573-752-3. The classic example of such a system is a fluid with temperature gradients in space causing heat to flow from hotter regions to colder ones, by the random but biased transport of the particles making up that fluid. In the modern literature the term Boltzmann equation is often used in a more general sense, referring to any kinetic equation that describes the change of a macroscopic quantity in a thermodynamic system, such as energy, charge or particle number. The equation arises not by analyzing the individual positions and momenta of each particle in the fluid but rather by considering a probability distribution for the p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Photon
A photon () is an elementary particle that is a quantum of the electromagnetic field, including electromagnetic radiation such as light and radio waves, and the force carrier for the electromagnetic force. Photons are massless particles that can move no faster than the speed of light measured in vacuum. The photon belongs to the class of boson particles. As with other elementary particles, photons are best explained by quantum mechanics and exhibit wave–particle duality, their behavior featuring properties of both waves and particles. The modern photon concept originated during the first two decades of the 20th century with the work of Albert Einstein, who built upon the research of Max Planck. While Planck was trying to explain how matter and electromagnetic radiation could be in thermal equilibrium with one another, he proposed that the energy stored within a material object should be regarded as composed of an integer number of discrete, equal-sized parts. To explain the pho ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compton Scattering
Compton scattering (or the Compton effect) is the quantum theory of high frequency photons scattering following an interaction with a charged particle, usually an electron. Specifically, when the photon hits electrons, it releases loosely bound electrons from the outer valence shells of atoms or molecules. The effect was discovered in 1923 by Arthur Holly Compton while researching the scattering of X-rays by light elements, and earned him the Nobel Prize in Physics in 1927. The Compton effect significantly deviated from dominating classical theories, using both special relativity and quantum mechanics to explain the interaction between high frequency photons and charged particles. Photons can interact with matter at the atomic level (e.g. photoelectric effect and Rayleigh scattering), at the nucleus, or with just an electron. Pair production and the Compton effect occur at the level of the electron. When a high frequency photon scatters due to an interaction with a charged part ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alexander Kompaneyets
Alexander Solomonovich Kompaneyets (Russian: Александр Соломонович Компанеец) was born on January 4, 1914, in Ekaterinoslav, Russian Empire (now Dnipro, Ukraine) and died on August 19, 1974, in Palanga, Lithuania. He was a prominent physicist, author of a number of textbooks, and collaborator on the Soviet atomic bomb project who lived mainly in Moscow. Life Kompaneyets was a student of Lev Landau in Kharkiv in the 1930s, where he dealt with solid state physics (electrical conductivity in metals and semiconductors). In 1936 he received his doctorate (candidate title) and habilitated in 1939 (Russian doctorate). He was a professor at the Institute of Chemical Physics at the Russian Academy of Sciences in Moscow (where he worked from 1946 until the end of his life) and is best known for his introductory textbook on theoretical physics. He also dealt with the physics of detonation, which he wrote about in a book with Yakov Zeldovich, and generally about ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bose–Einstein Statistics
In quantum statistics, Bose–Einstein statistics (B–E statistics) describes one of two possible ways in which a collection of non-interacting identical particles may occupy a set of available discrete energy states at thermodynamic equilibrium. The aggregation of particles in the same state, which is a characteristic of particles obeying Bose–Einstein statistics, accounts for the cohesive streaming of laser light and the frictionless creeping of superfluid helium. The theory of this behaviour was developed (1924–25) by Satyendra Nath Bose, who recognized that a collection of identical and indistinguishable particles could be distributed in this way. The idea was later adopted and extended by Albert Einstein in collaboration with Bose. Bose–Einstein statistics apply only to particles that do not follow the Pauli exclusion principle restrictions. Particles that follow Bose-Einstein statistics are called bosons, which have integer values of spin. In contrast, particles ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sunyaev–Zeldovich Effect
The Sunyaev–Zeldovich effect (named after Rashid Sunyaev and Yakov B. Zeldovich and often abbreviated as the SZ effect) is the spectral distortion of the cosmic microwave background (CMB) through inverse Compton scattering by high-energy electrons in galaxy clusters, in which the low-energy CMB photons receive an average energy boost during collision with the high-energy cluster electrons. Observed distortions of the cosmic microwave background spectrum are used to detect the disturbance of density in the universe. Using the Sunyaev–Zeldovich effect, dense clusters of galaxies have been observed. Overview The Sunyaev–Zeldovich effect was predicted by Rashid Sunyaev and Yakov Zeldovich to describe anisotropies in the CMB. The effect is caused by the CMB interacting with high energy electrons. These high energy electrons cause inverse Compton scattering of CMB photons which causes a distortion in the radiation spectrum of the CMB. The Sunyaev–Zeldovich effect is mos ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thomson Scattering
Thomson scattering is the elastic scattering of electromagnetic radiation by a free charged particle, as described by classical electromagnetism. It is the low-energy limit of Compton scattering: the particle's kinetic energy and photon frequency do not change as a result of the scattering. This limit is valid as long as the photon energy is much smaller than the mass energy of the particle: , or equivalently, if the wavelength of the light is much greater than the Compton wavelength of the particle (e.g., for electrons, longer wavelengths than hard x-rays). Description of the phenomenon Thomson scattering describes the classical limit of electromagnetic radiation scattering from a free particle. An incident plane wave accelerates a charged particle which consequently emits radiation of the same frequency. The net effect is to scatter the incident radiation. Thomson scattering is an important phenomenon in plasma physics and was first explained by the physicist J. J. Thomson ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Physical Cosmology
Physical cosmology is a branch of cosmology concerned with the study of cosmological models. A cosmological model, or simply cosmology, provides a description of the largest-scale structures and dynamics of the universe and allows study of fundamental questions about its Cosmogony, origin, structure, Chronology of the universe, evolution, and ultimate fate.For an overview, see Cosmology as a science originated with the Copernican principle, which implies that astronomical object, celestial bodies obey identical physical laws to those on Earth, and Newtonian mechanics, which first allowed those physical laws to be understood. Physical cosmology, as it is now understood, began in 1915 with the development of Albert Einstein's general relativity, general theory of relativity, followed by major observational discoveries in the 1920s: first, Edwin Hubble discovered that the universe contains a huge number of external Galaxy, galaxies beyond the Milky Way; then, work by Vesto Sliph ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transport Phenomena
In engineering, physics, and chemistry, the study of transport phenomena concerns the exchange of mass, energy, charge, momentum and angular momentum between observed and studied systems. While it draws from fields as diverse as continuum mechanics and thermodynamics, it places a heavy emphasis on the commonalities between the topics covered. Mass, momentum, and heat transport all share a very similar mathematical framework, and the parallels between them are exploited in the study of transport phenomena to draw deep mathematical connections that often provide very useful tools in the analysis of one field that are directly derived from the others. The fundamental analysis in all three subfields of mass, heat, and momentum transfer are often grounded in the simple principle that the total sum of the quantities being studied must be conserved by the system and its environment. Thus, the different phenomena that lead to transport are each considered individually with the knowled ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partial Differential Equations
In mathematics, a partial differential equation (PDE) is an equation which involves a multivariable function and one or more of its partial derivatives. The function is often thought of as an "unknown" that solves the equation, similar to how is thought of as an unknown number solving, e.g., an algebraic equation like . However, it is usually impossible to write down explicit formulae for solutions of partial differential equations. There is correspondingly a vast amount of modern mathematical and scientific research on methods to numerically approximate solutions of certain partial differential equations using computers. Partial differential equations also occupy a large sector of pure mathematical research, in which the usual questions are, broadly speaking, on the identification of general qualitative features of solutions of various partial differential equations, such as existence, uniqueness, regularity and stability. Among the many open questions are the existence an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |