|
Bose Gas
An ideal Bose gas is a quantum-mechanical phase of matter, analogous to a classical ideal gas. It is composed of bosons, which have an integer value of spin and abide by Bose–Einstein statistics. The statistical mechanics of bosons were developed by Satyendra Nath Bose for a photon gas and extended to massive particles by Albert Einstein, who realized that an ideal gas of bosons would form a condensate at a low enough temperature, unlike a classical ideal gas. This condensate is known as a Bose–Einstein condensate. Introduction and examples Bosons are quantum mechanical particles that follow Bose–Einstein statistics, or equivalently, that possess integer spin. These particles can be classified as elementary: these are the Higgs boson, the photon, the gluon, the W/Z and the hypothetical graviton; or composite like the atom of hydrogen, the atom of 16 O, the nucleus of deuterium, mesons etc. Additionally, some quasiparticles in more complex systems can also be co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Phase Of Matter
In the physical sciences, a phase is a region of material that is chemically uniform, physically distinct, and (often) mechanically separable. In a system consisting of ice and water in a glass jar, the ice cubes are one phase, the water is a second phase, and the humid air is a third phase over the ice and water. The glass of the jar is a different material, in its own separate phase. (See .) More precisely, a phase is a region of space (a thermodynamic system), throughout which all physical properties of a material are essentially uniform. Examples of physical properties include density, index of refraction, magnetization and chemical composition. The term ''phase'' is sometimes used as a synonym for state of matter, but there can be several immiscible phases of the same state of matter (as where oil and water separate into distinct phases, both in the liquid state). Types of phases Distinct phases may be described as different states of matter such as gas, liquid, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Oxygen
Oxygen is a chemical element; it has chemical symbol, symbol O and atomic number 8. It is a member of the chalcogen group (periodic table), group in the periodic table, a highly reactivity (chemistry), reactive nonmetal (chemistry), nonmetal, and a potent oxidizing agent that readily forms oxides with most elements as well as with other chemical compound, compounds. Oxygen is abundance of elements in Earth's crust, the most abundant element in Earth's crust, making up almost half of the Earth's crust in the form of various oxides such as water, carbon dioxide, iron oxides and silicates.Atkins, P.; Jones, L.; Laverman, L. (2016).''Chemical Principles'', 7th edition. Freeman. It is abundance of chemical elements, the third-most abundant element in the universe after hydrogen and helium. At standard temperature and pressure, two oxygen atoms will chemical bond, bind covalent bond, covalently to form dioxygen, a colorless and odorless diatomic gas with the chemical formula ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Helium-4
Helium-4 () is a stable isotope of the element helium. It is by far the more abundant of the two naturally occurring isotopes of helium, making up about 99.99986% of the helium on Earth. Its nucleus is identical to an alpha particle, and consists of two protons and two neutrons. Helium-4 makes up about one quarter of the ordinary matter in the universe by mass, with almost all of the rest being hydrogen. While nuclear fusion in stars also produces helium-4, most of the helium-4 in the Sun and in the universe is thought to have been produced during the Big Bang, known as " primordial helium". However, primordial helium-4 is largely absent from the Earth, having escaped during the high-temperature phase of Earth's formation. On Earth, most naturally occurring helium-4 is produced by the alpha decay of heavy elements in the Earth's crust, after the planet cooled and solidified. When liquid helium-4 is cooled to below , it becomes a superfluid, with properties very different from ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
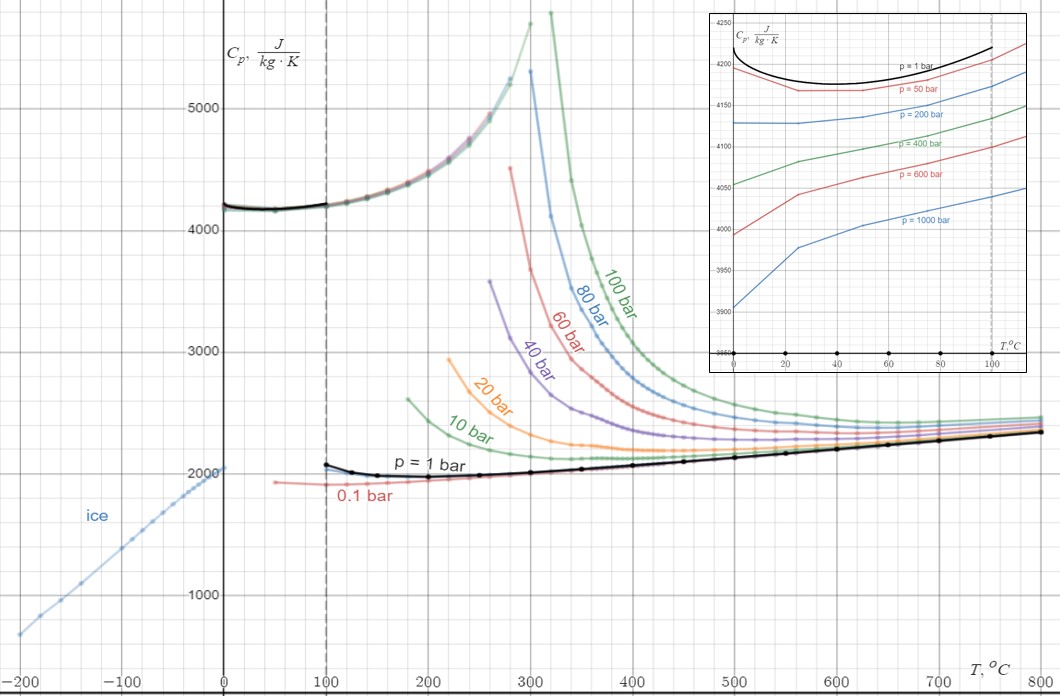
Heat Capacity
Heat capacity or thermal capacity is a physical property of matter, defined as the amount of heat to be supplied to an object to produce a unit change in its temperature. The SI unit of heat capacity is joule per kelvin (J/K). Heat capacity is an extensive property. The corresponding intensive property is the specific heat capacity, found by dividing the heat capacity of an object by its mass. Dividing the heat capacity by the amount of substance in moles yields its molar heat capacity. The volumetric heat capacity measures the heat capacity per volume. In architecture and civil engineering, the heat capacity of a building is often referred to as its '' thermal mass''. Definition Basic definition The heat capacity of an object, denoted by C, is the limit C = \lim_\frac, where \Delta Q is the amount of heat that must be added to the object (of mass ''M'') in order to raise its temperature by \Delta T. The value of this parameter usually varies considerably depending o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Peter Debye
Peter Joseph William Debye ( ; born Petrus Josephus Wilhelmus Debije, ; March 24, 1884 – November 2, 1966) was a Dutch-American physicist and physical chemist, and Nobel laureate in Chemistry. Biography Early life Born in Maastricht, Netherlands, Debye enrolled in the Aachen University of Technology in 1901. In 1905, he completed his first degree in electrical engineering. He published his first paper, a mathematically elegant solution of a problem involving eddy currents, in 1907. At Aachen, he studied under the theoretical physicist Arnold Sommerfeld, who later claimed that his most important discovery was Peter Debye. In 1906, Sommerfeld received an appointment at Munich, Bavaria, and took Debye with him as his assistant. Debye got his Ph.D. with a dissertation on radiation pressure in 1908. In 1910, he derived the Planck radiation formula using a method which Max Planck agreed was simpler than his own. In 1911, when Albert Einstein took an appointment as a profes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Normal Mode
A normal mode of a dynamical system is a pattern of motion in which all parts of the system move sinusoidally with the same frequency and with a fixed phase relation. The free motion described by the normal modes takes place at fixed frequencies. These fixed frequencies of the normal modes of a system are known as its natural frequencies or resonant frequencies. A physical object, such as a building, bridge, or molecule, has a set of normal modes and their natural frequencies that depend on its structure, materials and boundary conditions. The most general motion of a linear system is a superposition of its normal modes. The modes are normal in the sense that they can move independently, that is to say that an excitation of one mode will never cause motion of a different mode. In mathematical terms, normal modes are orthogonal to each other. General definitions Mode In the wave theory of physics and engineering, a mode in a dynamical system is a standing wave st ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Debye Model
In thermodynamics and solid-state physics, the Debye model is a method developed by Peter Debye in 1912 to estimate phonon contribution to the specific heat ( heat capacity) in a solid. It treats the vibrations of the atomic lattice (heat) as phonons in a box in contrast to the Einstein photoelectron model, which treats the solid as many individual, non-interacting quantum harmonic oscillators. The Debye model correctly predicts the low-temperature dependence of the heat capacity of solids, which is proportional to the cube of temperature – the Debye ''T'' 3 law. Similarly to the Einstein photoelectron model, it recovers the Dulong–Petit law at high temperatures. Due to simplifying assumptions, its accuracy suffers at intermediate temperatures. Derivation The Debye model treats atomic vibrations as phonons confined in the solid's volume. It is analogous to Planck's law of black body radiation, which treats electromagnetic radiation as a photon gas confined in a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Phonon
A phonon is a collective excitation in a periodic, elastic arrangement of atoms or molecules in condensed matter, specifically in solids and some liquids. In the context of optically trapped objects, the quantized vibration mode can be defined as phonons as long as the modal wavelength of the oscillation is smaller than the size of the object. A type of quasiparticle in physics, a phonon is an excited state in the quantum mechanical quantization of the modes of vibrations for elastic structures of interacting particles. Phonons can be thought of as quantized sound waves, similar to photons as quantized light waves. The study of phonons is an important part of condensed matter physics. They play a major role in many of the physical properties of condensed matter systems, such as thermal conductivity and electrical conductivity, as well as in models of neutron scattering and related effects. The concept of phonons was introduced in 1930 by Soviet physicist Igor Tamm. The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
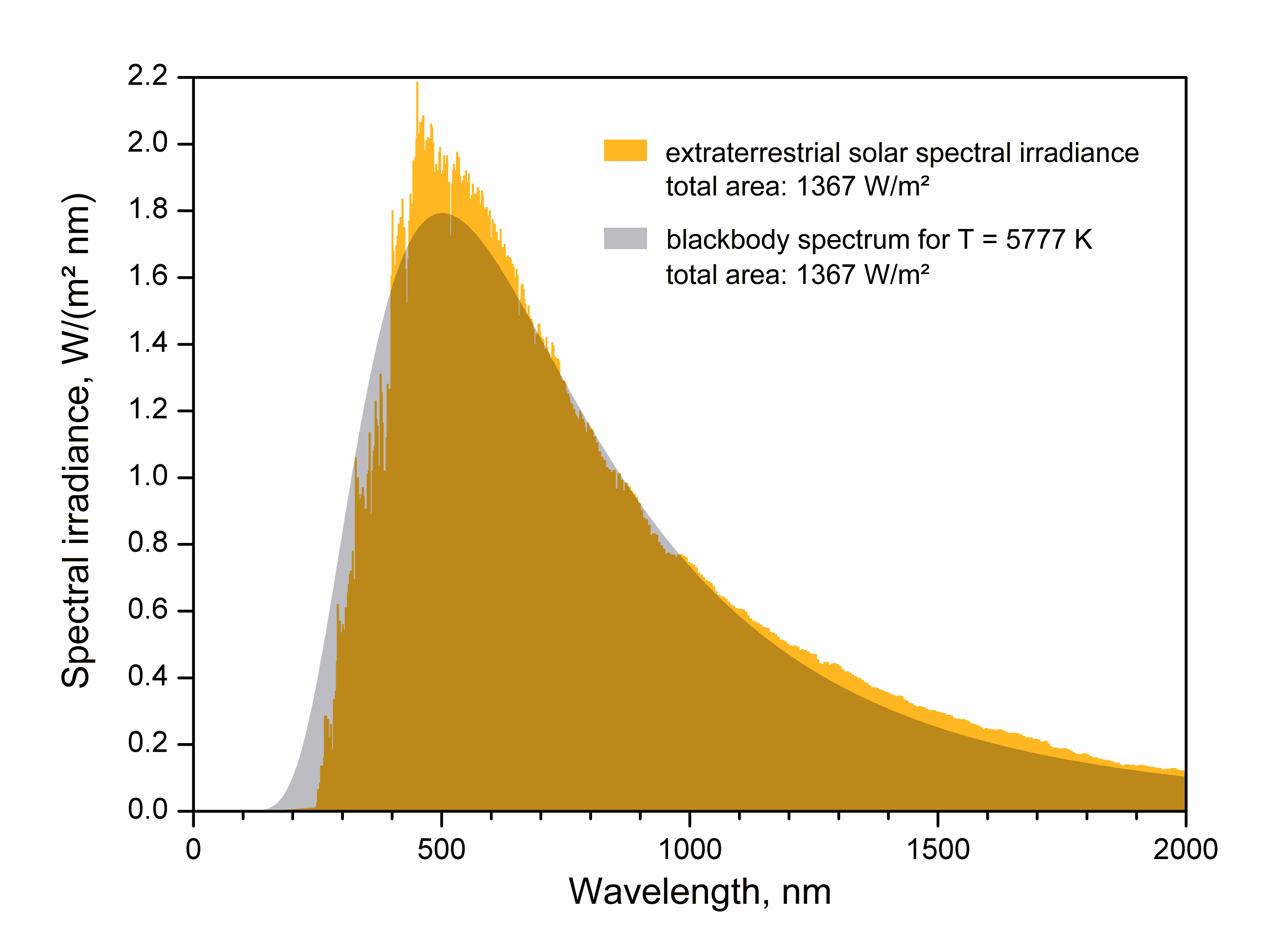
Black-body Radiation
Black-body radiation is the thermal radiation, thermal electromagnetic radiation within, or surrounding, a body in thermodynamic equilibrium with its environment, emitted by a black body (an idealized opaque, non-reflective body). It has a specific continuous spectrum that depends only on the body's temperature., Chapter 13. A perfectly-insulated enclosure which is in thermal equilibrium internally contains blackbody radiation and will emit it through a hole made in its wall, provided the hole is small enough to have a negligible effect upon the equilibrium. The thermal radiation spontaneously emitted by many ordinary objects can be approximated as blackbody radiation. Of particular importance, although planets and stars (including the Earth and Sun) are neither in thermal equilibrium with their surroundings nor perfect black bodies, blackbody radiation is still a good first approximation for the energy they emit. The term ''black body'' was introduced by Gustav Kirchhoff in 1860. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Planck's Law
In physics, Planck's law (also Planck radiation law) describes the spectral density of electromagnetic radiation emitted by a black body in thermal equilibrium at a given temperature , when there is no net flow of matter or energy between the body and its environment. At the end of the 19th century, physicists were unable to explain why the observed spectrum of black-body radiation, which by then had been accurately measured, diverged significantly at higher frequencies from that predicted by existing theories. In 1900, German physicist Max Planck heuristically derived a formula for the observed spectrum by assuming that a hypothetical electrically charged oscillator in a cavity that contained black-body radiation could only change its energy in a minimal increment, , that was proportional to the frequency of its associated electromagnetic wave. While Planck originally regarded the hypothesis of dividing energy into increments as a mathematical artifice, introduced merely to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Plasma Oscillation
Plasma oscillations, also known as Langmuir waves (after Irving Langmuir), are rapid oscillations of the electron density in conducting media such as plasmas or metals in the ultraviolet region. The oscillations can be described as an instability in the dielectric function of a free electron gas. The frequency depends only weakly on the wavelength of the oscillation. The quasiparticle resulting from the quantization of these oscillations is the '' plasmon''. Langmuir waves were discovered by American physicists Irving Langmuir and Lewi Tonks in the 1920s. They are parallel in form to Jeans instability waves, which are caused by gravitational instabilities in a static medium. Mechanism Consider an electrically neutral plasma in equilibrium, consisting of a gas of positively charged ions and negatively charged electrons. If one displaces by a tiny amount an electron or a group of electrons with respect to the ions, the Coulomb force pulls the electrons back, acting as a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Plasmon
In physics, a plasmon is a quantum of plasma oscillation. Just as light (an optical oscillation) consists of photons, the plasma oscillation consists of plasmons. The plasmon can be considered as a quasiparticle since it arises from the quantization of plasma oscillations, just like phonons are quantizations of mechanical vibrations. Thus, plasmons are collective (a discrete number) oscillations of the free electron gas density. For example, at optical frequencies, plasmons can couple with a photon to create another quasiparticle called a plasmon polariton. The field of study and manipulation of plasmons is called plasmonics. Derivation The plasmon was initially proposed in 1952 by David Pines and David Bohm and was shown to arise from a Hamiltonian for the long-range electron-electron correlations. Since plasmons are the quantization of classical plasma oscillations, most of their properties can be derived directly from Maxwell's equations. Explanation Plasmons ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |