Bivector on:
[Wikipedia]
[Google]
[Amazon]
 In
In
 The rotation vector is an example of an
The rotation vector is an example of an
 As suggested by their name and that of the algebra, bivectors have a natural geometric interpretation. This appies in any dimension number but is best illustrated in three, where parallels can be drawn with more familiar objects. In two dimensions the geometric interpretation is trivial, as the space is two-dimensional so has only one plane, and all bivectors are associated with it differing only by a scalar factor.
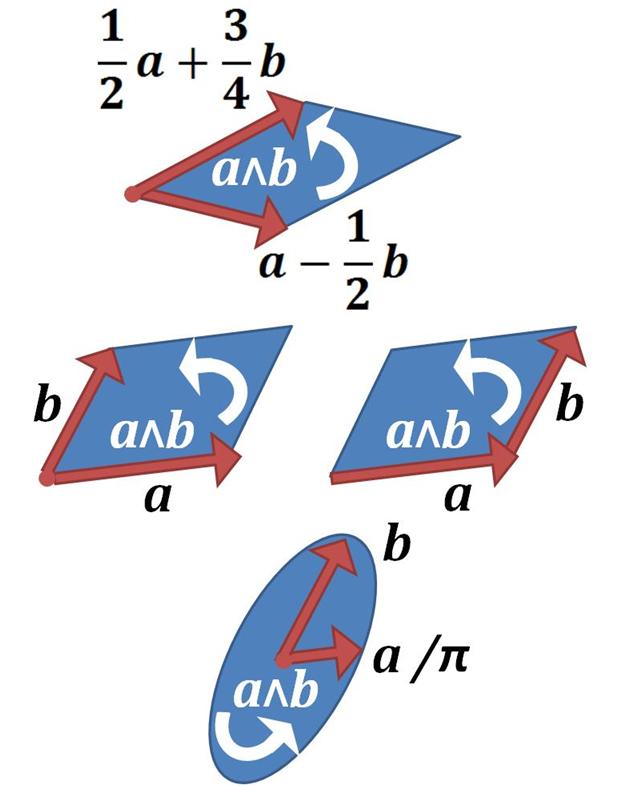
All bivectors can be interpreted as planes, or more precisely as directed plane segments. In three dimensions, there are three properties of a bivector that can be interpreted geometrically:
* The arrangement of the plane in space, precisely the
As suggested by their name and that of the algebra, bivectors have a natural geometric interpretation. This appies in any dimension number but is best illustrated in three, where parallels can be drawn with more familiar objects. In two dimensions the geometric interpretation is trivial, as the space is two-dimensional so has only one plane, and all bivectors are associated with it differing only by a scalar factor.
All bivectors can be interpreted as planes, or more precisely as directed plane segments. In three dimensions, there are three properties of a bivector that can be interpreted geometrically:
* The arrangement of the plane in space, precisely the  In three dimensions, every bivector can be generated by the exterior product of two vectors. If the bivector then the magnitude of is
:
where is the angle between the vectors. This is the area of the
In three dimensions, every bivector can be generated by the exterior product of two vectors. If the bivector then the magnitude of is
:
where is the angle between the vectors. This is the area of the 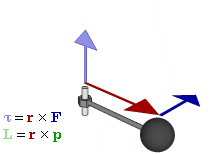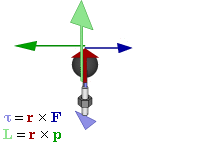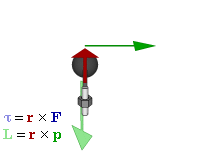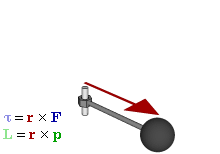 In three dimensions, Hodge duality relates the
In three dimensions, Hodge duality relates the  Bivectors can be added together as areas. Given two non-zero bivectors and in three dimensions it is always possible to find a vector that is contained in both, say, so the bivectors can be written as exterior products involving :
:
This can be interpreted geometrically as seen in the diagram: the two areas sum to give a third, with the three areas forming faces of a prism with , , and as edges. This corresponds to the two ways of calculating the area using the
Bivectors can be added together as areas. Given two non-zero bivectors and in three dimensions it is always possible to find a vector that is contained in both, say, so the bivectors can be written as exterior products involving :
:
This can be interpreted geometrically as seen in the diagram: the two areas sum to give a third, with the three areas forming faces of a prism with , , and as edges. This corresponds to the two ways of calculating the area using the
 The rotations generated are more complex though. They can be categorised as follows:
: ''
The rotations generated are more complex though. They can be categorised as follows:
: ''
mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ...
, a bivector or 2-vector is a quantity in exterior algebra
In mathematics, the exterior algebra or Grassmann algebra of a vector space V is an associative algebra that contains V, which has a product, called exterior product or wedge product and denoted with \wedge, such that v\wedge v=0 for every vector ...
or geometric algebra
In mathematics, a geometric algebra (also known as a Clifford algebra) is an algebra that can represent and manipulate geometrical objects such as vectors. Geometric algebra is built out of two fundamental operations, addition and the geometric pr ...
that extends the idea of scalars and vector
Vector most often refers to:
* Euclidean vector, a quantity with a magnitude and a direction
* Disease vector, an agent that carries and transmits an infectious pathogen into another living organism
Vector may also refer to:
Mathematics a ...
s. Considering a scalar as a degree-zero quantity and a vector as a degree-one quantity, a bivector is of degree two. Bivectors have applications in many areas of mathematics and physics. They are related to complex number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the for ...
s in two dimensions and to both pseudovector
In physics and mathematics, a pseudovector (or axial vector) is a quantity that transforms like a vector under continuous rigid transformations such as rotations or translations, but which does ''not'' transform like a vector under certain ' ...
s and vector quaternion
In mathematics, the quaternion number system extends the complex numbers. Quaternions were first described by the Irish mathematician William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space. The algebra of quaternions ...
s in three dimensions. They can be used to generate rotation
Rotation or rotational/rotary motion is the circular movement of an object around a central line, known as an ''axis of rotation''. A plane figure can rotate in either a clockwise or counterclockwise sense around a perpendicular axis intersect ...
s in a space of any number of dimensions, and are a useful tool for classifying such rotations.
Geometrically, a simple bivector can be interpreted as characterizing a directed plane segment (or oriented plane segment), much as vector
Vector most often refers to:
* Euclidean vector, a quantity with a magnitude and a direction
* Disease vector, an agent that carries and transmits an infectious pathogen into another living organism
Vector may also refer to:
Mathematics a ...
s can be thought of as characterizing '' directed line segments''.
The bivector has an ''attitude
Attitude or Attitude may refer to:
Philosophy and psychology
* Attitude (psychology), a disposition or state of mind
** Attitude change
* Propositional attitude, a mental state held towards a proposition
Science and technology
* Orientation ...
'' (or direction) of the plane spanned by and , has an area that is a scalar multiple of any reference plane segment with the same attitude (and in geometric algebra, it has a ''magnitude'' equal to the area of the parallelogram
In Euclidean geometry, a parallelogram is a simple polygon, simple (non-list of self-intersecting polygons, self-intersecting) quadrilateral with two pairs of Parallel (geometry), parallel sides. The opposite or facing sides of a parallelogram a ...
with edges and ), and has an ''orientation'' being the side of on which lies within the plane spanned by and .
In layman terms, any surface defines the same bivector if it is parallel to the same plane (same attitude), has the same area, and same orientation (see figure).
Bivectors are generated by the exterior product
In mathematics, specifically in topology,
the interior of a subset of a topological space is the union of all subsets of that are open in .
A point that is in the interior of is an interior point of .
The interior of is the complement of ...
on vectors: given two vectors and , their exterior product is a bivector, as is any sum of bivectors. Not all bivectors can be expressed as an exterior product without such summation. More precisely, a bivector that can be expressed as an exterior product is called ''simple''; in up to three dimensions all bivectors are simple, but in higher dimensions this is not the case. The exterior product of two vectors is alternating, so is the zero bivector, and , producing the opposite orientation. Concepts directly related to bivector are rank-2 antisymmetric tensor In mathematics and theoretical physics, a tensor is antisymmetric or alternating on (or with respect to) an index subset if it alternates sign (+/−) when any two indices of the subset are interchanged. section §7. The index subset must generally ...
and skew-symmetric matrix
In mathematics, particularly in linear algebra, a skew-symmetric (or antisymmetric or antimetric) matrix is a square matrix whose transpose equals its negative. That is, it satisfies the condition
In terms of the entries of the matrix, if a ...
.
History
The bivector was first defined in 1844 by German mathematicianHermann Grassmann
Hermann Günther Grassmann (, ; 15 April 1809 – 26 September 1877) was a German polymath known in his day as a linguist and now also as a mathematician. He was also a physicist, general scholar, and publisher. His mathematical work was littl ...
in exterior algebra
In mathematics, the exterior algebra or Grassmann algebra of a vector space V is an associative algebra that contains V, which has a product, called exterior product or wedge product and denoted with \wedge, such that v\wedge v=0 for every vector ...
as the result of the exterior product
In mathematics, specifically in topology,
the interior of a subset of a topological space is the union of all subsets of that are open in .
A point that is in the interior of is an interior point of .
The interior of is the complement of ...
of two vectors. Just the previous year, in Ireland, William Rowan Hamilton
Sir William Rowan Hamilton (4 August 1805 – 2 September 1865) was an Irish astronomer, mathematician, and physicist who made numerous major contributions to abstract algebra, classical mechanics, and optics. His theoretical works and mathema ...
had discovered quaternions
In mathematics, the quaternion number system extends the complex numbers. Quaternions were first described by the Irish mathematician William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space. The algebra of quaternion ...
. Hamilton coined both ''vector'' and ''bivector'', the latter in his ''Lectures on Quaternions'' (1853) as he introduced biquaternion
In abstract algebra, the biquaternions are the numbers , where , and are complex numbers, or variants thereof, and the elements of multiply as in the quaternion group and commute with their coefficients. There are three types of biquaternions cor ...
s, which have bivectors for their vector parts. It was not until English mathematician William Kingdon Clifford
William Kingdon Clifford (4 May 18453 March 1879) was a British mathematician and philosopher. Building on the work of Hermann Grassmann, he introduced what is now termed geometric algebra, a special case of the Clifford algebra named in his ...
in 1888 added the geometric product to Grassmann's algebra, incorporating the ideas of both Hamilton and Grassmann, and founded Clifford algebra
In mathematics, a Clifford algebra is an algebra generated by a vector space with a quadratic form, and is a unital associative algebra with the additional structure of a distinguished subspace. As -algebras, they generalize the real number ...
, that the bivector of this article arose. Henry Forder used the term ''bivector'' to develop exterior algebra in 1941.
In the 1890s Josiah Willard Gibbs
Josiah Willard Gibbs (; February 11, 1839 – April 28, 1903) was an American mechanical engineer and scientist who made fundamental theoretical contributions to physics, chemistry, and mathematics. His work on the applications of thermodynami ...
and Oliver Heaviside
Oliver Heaviside ( ; 18 May 1850 – 3 February 1925) was an English mathematician and physicist who invented a new technique for solving differential equations (equivalent to the Laplace transform), independently developed vector calculus, an ...
developed vector calculus
Vector calculus or vector analysis is a branch of mathematics concerned with the differentiation and integration of vector fields, primarily in three-dimensional Euclidean space, \mathbb^3. The term ''vector calculus'' is sometimes used as a ...
, which included separate cross product
In mathematics, the cross product or vector product (occasionally directed area product, to emphasize its geometric significance) is a binary operation on two vectors in a three-dimensional oriented Euclidean vector space (named here E), and ...
and dot product
In mathematics, the dot product or scalar productThe term ''scalar product'' means literally "product with a Scalar (mathematics), scalar as a result". It is also used for other symmetric bilinear forms, for example in a pseudo-Euclidean space. N ...
s that were derived from quaternion multiplication.
A discussion of quaternions from these years is at: The success of vector calculus, and of the book ''Vector Analysis
Vector calculus or vector analysis is a branch of mathematics concerned with the differentiation and integration of vector fields, primarily in three-dimensional Euclidean space, \mathbb^3. The term ''vector calculus'' is sometimes used as a ...
'' by Gibbs and Wilson, had the effect that the insights of Hamilton and Clifford were overlooked for a long time, since much of 20th century mathematics and physics was formulated in vector terms. Gibbs used vectors to fill the role of bivectors in three dimensions, and used bivector in Hamilton's sense, a use that has sometimes been copied.
Today the bivector is largely studied as a topic in geometric algebra
In mathematics, a geometric algebra (also known as a Clifford algebra) is an algebra that can represent and manipulate geometrical objects such as vectors. Geometric algebra is built out of two fundamental operations, addition and the geometric pr ...
, a Clifford algebra over real or complex
Complex commonly refers to:
* Complexity, the behaviour of a system whose components interact in multiple ways so possible interactions are difficult to describe
** Complex system, a system composed of many components which may interact with each ...
vector space
In mathematics and physics, a vector space (also called a linear space) is a set (mathematics), set whose elements, often called vector (mathematics and physics), ''vectors'', can be added together and multiplied ("scaled") by numbers called sc ...
s with a quadratic form
In mathematics, a quadratic form is a polynomial with terms all of degree two (" form" is another name for a homogeneous polynomial). For example,
4x^2 + 2xy - 3y^2
is a quadratic form in the variables and . The coefficients usually belong t ...
. Its resurgence was led by David Hestenes who, along with others, applied geometric algebra to a range of new applications in physics
Physics is the scientific study of matter, its Elementary particle, fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge whi ...
.
Derivation
For this article, the bivector will be considered only in real geometric algebras, which may be applied in most areas of physics. Also unless otherwise stated, all examples have aEuclidean metric
In mathematics, the Euclidean distance between two points in Euclidean space is the length of the line segment between them. It can be calculated from the Cartesian coordinates of the points using the Pythagorean theorem, and therefore is oc ...
and so a positive-definite In mathematics, positive definiteness is a property of any object to which a bilinear form or a sesquilinear form may be naturally associated, which is positive-definite. See, in particular:
* Positive-definite bilinear form
* Positive-definite ...
quadratic form
In mathematics, a quadratic form is a polynomial with terms all of degree two (" form" is another name for a homogeneous polynomial). For example,
4x^2 + 2xy - 3y^2
is a quadratic form in the variables and . The coefficients usually belong t ...
.
Geometric algebra and the geometric product
The bivector arises from the definition of the geometric product over a vector space with an associated quadratic form sometimes called the ''metric''. For vectors , and , the geometric product satisfies the following properties: ;Associativity
In mathematics, the associative property is a property of some binary operations that rearranging the parentheses in an expression will not change the result. In propositional logic, associativity is a Validity (logic), valid rule of replaceme ...
:
; Left and right distributivity
In mathematics, the distributive property of binary operations is a generalization of the distributive law, which asserts that the equality
x \cdot (y + z) = x \cdot y + x \cdot z
is always true in elementary algebra.
For example, in elementary ...
:
; Scalar square : , where is the quadratic form, which need not be positive-definite In mathematics, positive definiteness is a property of any object to which a bilinear form or a sesquilinear form may be naturally associated, which is positive-definite. See, in particular:
* Positive-definite bilinear form
* Positive-definite ...
.
Scalar product
From associativity, , is a scalar times . When is not parallel to and hence not a scalar multiple of , cannot be a scalar. But : is a sum of scalars and so a scalar. From thelaw of cosines
In trigonometry, the law of cosines (also known as the cosine formula or cosine rule) relates the lengths of the sides of a triangle to the cosine of one of its angles. For a triangle with sides , , and , opposite respective angles , , and (see ...
on the triangle formed by the vectors its value is , where is the angle between the vectors. It is therefore identical to the scalar product between two vectors, and is written the same way,
:
It is symmetric, scalar-valued, and can be used to determine the angle between two vectors: in particular if and are orthogonal the product is zero.
Exterior product
Just as the scalar product can be formulated as the symmetric part of the geometric product of another quantity, the exterior product (sometimes known as the "wedge" or "progressive" product) can be formulated as its antisymmetric part: : It is antisymmetric in and : and by addition: : That is, the geometric product is the sum of the symmetric scalar product and alternating exterior product. To examine the nature of , consider the formula : which using thePythagorean trigonometric identity
The Pythagorean trigonometric identity, also called simply the Pythagorean identity, is an identity expressing the Pythagorean theorem in terms of trigonometric functions. Along with the sum-of-angles formulae, it is one of the basic relations ...
gives the value of
:
With a negative square, it cannot be a scalar or vector quantity, so it is a new sort of object, a bivector. It has magnitude
Magnitude may refer to:
Mathematics
*Euclidean vector, a quantity defined by both its magnitude and its direction
*Magnitude (mathematics), the relative size of an object
*Norm (mathematics), a term for the size or length of a vector
*Order of ...
, where is the angle between the vectors, and so is zero for parallel vectors.
To distinguish them from vectors, bivectors are written here with bold capitals, for example:
:
although other conventions are used, in particular as vectors and bivectors are both elements of the geometric algebra.
Properties
The algebra generated by the geometric product (that is, all objects formed by taking repeated sums and geometric products of scalars and vectors) is thegeometric algebra
In mathematics, a geometric algebra (also known as a Clifford algebra) is an algebra that can represent and manipulate geometrical objects such as vectors. Geometric algebra is built out of two fundamental operations, addition and the geometric pr ...
over the vector space. For an Euclidean vector space, this algebra is written or , where is the dimension of the vector space . is both a vector space and an algebra, generated by all the products between vectors in , so it contains all vectors and bivectors. More precisely, as a vector space it contains the vectors and bivectors as linear subspace
In mathematics, the term ''linear'' is used in two distinct senses for two different properties:
* linearity of a ''function (mathematics), function'' (or ''mapping (mathematics), mapping'');
* linearity of a ''polynomial''.
An example of a li ...
s, though not as subalgebra In mathematics, a subalgebra is a subset of an algebra, closed under all its operations, and carrying the induced operations.
"Algebra", when referring to a structure, often means a vector space or module equipped with an additional bilinear opera ...
s (since the geometric product of two vectors is not generally another vector).
The space ⋀2R''n''
The space of all bivectors has dimension and is written , and is the secondexterior power
In mathematics, the exterior algebra or Grassmann algebra of a vector space V is an associative algebra that contains V, which has a product, called exterior product or wedge product and denoted with \wedge, such that v\wedge v=0 for every vector ...
of the original vector space.
Even subalgebra
The subalgebra generated by the bivectors is the ''even subalgebra'' of the geometric algebra, written . This algebra results from considering all repeated sums and geometric products of scalars and bivectors. It has dimension , and contains as a linear subspace. In two and three dimensions the even subalgebra contains only scalars and bivectors, and each is of particular interest. In two dimensions, the even subalgebra isisomorphic
In mathematics, an isomorphism is a structure-preserving mapping or morphism between two structures of the same type that can be reversed by an inverse mapping. Two mathematical structures are isomorphic if an isomorphism exists between the ...
to the complex number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the for ...
s, , while in three it is isomorphic to the quaternion
In mathematics, the quaternion number system extends the complex numbers. Quaternions were first described by the Irish mathematician William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space. The algebra of quater ...
s, . The even subalgebra contains the rotation
Rotation or rotational/rotary motion is the circular movement of an object around a central line, known as an ''axis of rotation''. A plane figure can rotate in either a clockwise or counterclockwise sense around a perpendicular axis intersect ...
s in any dimension.
Magnitude
As noted in the previous section the magnitude of a simple bivector, that is one that is the exterior product of two vectors and , is , where is the angle between the vectors. It is written , where is the bivector. For general bivectors, the magnitude can be calculated by taking the norm of the bivector considered as a vector in the space . If the magnitude is zero then all the bivector's components are zero, and the bivector is the zero bivector which as an element of the geometric algebra equals the scalar zero.Unit bivectors
A unit bivector is one with unit magnitude. Such a bivector can be derived from any non-zero bivector by dividing the bivector by its magnitude, that is : Of particular utility are the unit bivectors formed from the products of thestandard basis
In mathematics, the standard basis (also called natural basis or canonical basis) of a coordinate vector space (such as \mathbb^n or \mathbb^n) is the set of vectors, each of whose components are all zero, except one that equals 1. For exampl ...
of the vector space. If and are distinct basis vectors then the product is a bivector. As and are orthogonal, , written , and has unit magnitude as the vectors are unit vector
In mathematics, a unit vector in a normed vector space is a Vector (mathematics and physics), vector (often a vector (geometry), spatial vector) of Norm (mathematics), length 1. A unit vector is often denoted by a lowercase letter with a circumfle ...
s. The set of all bivectors produced from the basis in this way form a basis for . For instance, in four dimensions the basis for is (, , , , , ) or (, , , , , ).
Simple bivectors
The exterior product of two vectors is a bivector, but not all bivectors are exterior products of two vectors. For example, in four dimensions the bivector : cannot be written as the exterior product of two vectors. A bivector that can be written as the exterior product of two vectors is simple. In two and three dimensions all bivectors are simple, but not in four or more dimensions; in four dimensions every bivector is the sum of at most two exterior products. A bivector has a real square if and only if it is simple, and only simple bivectors can be represented geometrically by a directed plane area.Product of two bivectors
The geometric product of two bivectors, and , is : The quantity is the scalar-valued scalar product, while is the grade 4 exterior product that arises in four or more dimensions. The quantity is the bivector-valuedcommutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.
Group theory
The commutator of two elements, ...
product, given by
:
The space of bivectors is a Lie algebra
In mathematics, a Lie algebra (pronounced ) is a vector space \mathfrak g together with an operation called the Lie bracket, an alternating bilinear map \mathfrak g \times \mathfrak g \rightarrow \mathfrak g, that satisfies the Jacobi ident ...
over , with the commutator product as the Lie bracket. The full geometric product of bivectors generates the even subalgebra.
Of particular interest is the product of a bivector with itself. As the commutator product is antisymmetric the product simplifies to
:
If the bivector is ''simple'' the last term is zero and the product is the scalar-valued , which can be used as a check for simplicity. In particular the exterior product of bivectors only exists in four or more dimensions, so all bivectors in two and three dimensions are simple.
General bivectors and matrices
Bivectors are isomorphic to skew-symmetric matrices in any number of dimensions. For example, the general bivector in three dimensions maps to the matrix : This multiplied by vectors on both sides gives the same vector as the product of a vector and bivector minus the exterior product; an example is the angular velocity tensor. Skew symmetric matrices generate orthogonal matrices withdeterminant
In mathematics, the determinant is a Scalar (mathematics), scalar-valued function (mathematics), function of the entries of a square matrix. The determinant of a matrix is commonly denoted , , or . Its value characterizes some properties of the ...
through the exponential map. In particular, applying the exponential map to a bivector that is associated with a rotation yields a rotation matrix
In linear algebra, a rotation matrix is a transformation matrix that is used to perform a rotation (mathematics), rotation in Euclidean space. For example, using the convention below, the matrix
:R = \begin
\cos \theta & -\sin \theta \\
\sin \t ...
. The rotation matrix given by the skew-symmetric matrix above is
:
The rotation described by is the same as that described by the rotor given by
:
and the matrix can be also calculated directly from rotor . In three dimensions, this is given by
:
Bivectors are related to the eigenvalue
In linear algebra, an eigenvector ( ) or characteristic vector is a vector that has its direction unchanged (or reversed) by a given linear transformation. More precisely, an eigenvector \mathbf v of a linear transformation T is scaled by a ...
s of a rotation matrix. Given a rotation matrix the eigenvalues can be calculated by solving the characteristic equation for that matrix . By the fundamental theorem of algebra
The fundamental theorem of algebra, also called d'Alembert's theorem or the d'Alembert–Gauss theorem, states that every non-constant polynomial, constant single-variable polynomial with Complex number, complex coefficients has at least one comp ...
this has three roots (only one of which is real as there is only one eigenvector, i.e., the axis of rotation). The other roots must be a complex conjugate pair. They have unit magnitude so purely imaginary logarithms, equal to the magnitude of the bivector associated with the rotation, which is also the angle of rotation. The eigenvectors associated with the complex eigenvalues are in the plane of the bivector, so the exterior product of two non-parallel eigenvectors results in the bivector (or a multiple thereof).
Two dimensions
When working with coordinates in geometric algebra it is usual to write the basis vectors as (, a convention that will be used here. Avector
Vector most often refers to:
* Euclidean vector, a quantity with a magnitude and a direction
* Disease vector, an agent that carries and transmits an infectious pathogen into another living organism
Vector may also refer to:
Mathematics a ...
in real two-dimensional space can be written , where and are real numbers, and are orthonormal
In linear algebra, two vectors in an inner product space are orthonormal if they are orthogonal unit vectors. A unit vector means that the vector has a length of 1, which is also known as normalized. Orthogonal means that the vectors are all perpe ...
basis vectors. The geometric product of two such vectors is
:
This can be split into the symmetric, scalar-valued, scalar product and an antisymmetric, bivector-valued exterior product:
:
All bivectors in two dimensions are of this form, that is multiples of the bivector , written to emphasise it is a bivector rather than a vector. The magnitude of is , with
:
so it is called the unit bivector. The term unit bivector can be used in other dimensions but it is only uniquely defined (up to a sign) in two dimensions and all bivectors are multiples of . As the highest grade element of the algebra is also the pseudoscalar
In linear algebra, a pseudoscalar is a quantity that behaves like a scalar, except that it changes sign under a parity inversion while a true scalar does not.
A pseudoscalar, when multiplied by an ordinary vector, becomes a '' pseudovector'' ...
which is given the symbol .
Complex numbers
With the properties of negative square and unit magnitude, the unit bivector can be identified with theimaginary unit
The imaginary unit or unit imaginary number () is a mathematical constant that is a solution to the quadratic equation Although there is no real number with this property, can be used to extend the real numbers to what are called complex num ...
from complex numbers
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the form a ...
. The bivectors and scalars together form the even subalgebra of the geometric algebra, which is isomorphic
In mathematics, an isomorphism is a structure-preserving mapping or morphism between two structures of the same type that can be reversed by an inverse mapping. Two mathematical structures are isomorphic if an isomorphism exists between the ...
to the complex numbers . The even subalgebra has basis , the whole algebra has basis .
The complex numbers are usually identified with the coordinate axes
In geometry, a coordinate system is a system that uses one or more numbers, or coordinates, to uniquely determine and standardize the position of the points or other geometric elements on a manifold such as Euclidean space. The coordinates are ...
and two-dimensional vectors, which would mean associating them with the vector elements of the geometric algebra. There is no contradiction in this, as to get from a general vector to a complex number an axis needs to be identified as the real axis, say. This multiplies by all vectors to generate the elements of even subalgebra.
All the properties of complex numbers can be derived from bivectors, but two are of particular interest. First as with complex numbers products of bivectors and so the even subalgebra are commutative
In mathematics, a binary operation is commutative if changing the order of the operands does not change the result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it. Perhaps most familiar as a pr ...
. This is only true in two dimensions, so properties of the bivector in two dimensions that depend on commutativity do not usually generalise to higher dimensions.
Second a general bivector can be written
:
where is a real number. Putting this into the Taylor series
In mathematics, the Taylor series or Taylor expansion of a function is an infinite sum of terms that are expressed in terms of the function's derivatives at a single point. For most common functions, the function and the sum of its Taylor ser ...
for the exponential map and using the property results in a bivector version of Euler's formula
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the fundamental relationship between the trigonometric functions and the complex exponential function. Euler's formula states that, for ...
,
:
which when multiplied by any vector rotates it through an angle about the origin:
:
The product of a vector with a bivector in two dimensions is anticommutative, so the following products all generate the same rotation
:
Of these the last product is the one that generalises into higher dimensions. The quantity needed is called a rotor
ROTOR was an elaborate air defence radar system built by the British Government in the early 1950s to counter possible attack by Soviet bombers. To get it operational as quickly as possible, it was initially made up primarily of WWII-era syst ...
and is given the symbol , so in two dimensions a rotor that rotates through angle can be written
:
and the rotation it generates is
:
Three dimensions
In three dimensions the geometric product of two vectors is : This can be split into the symmetric, scalar-valued, scalar product and the antisymmetric, bivector-valued, exterior product: : In three dimensions all bivectors are simple and so the result of an exterior product. The unit bivectors , and form a basis for the space of bivectors , which is itself a three-dimensional linear space. So if a general bivector is: : they can be added like vectors : while when multiplied they produce the following : which can be split into symmetric scalar and antisymmetric bivector parts as follows : The exterior product of two bivectors in three dimensions is zero. A bivector can be written as the product of its magnitude and a unit bivector, so writing for and using the Taylor series for the exponential map it can be shown that : This is another version of Euler's formula, but with a general bivector in three dimensions. Unlike in two dimensions bivectors are not commutative so properties that depend on commutativity do not apply in three dimensions. For example, in general in three (or more) dimensions. The full geometric algebra in three dimensions, , has basis (, , , , , , , ). The element is a trivector and thepseudoscalar
In linear algebra, a pseudoscalar is a quantity that behaves like a scalar, except that it changes sign under a parity inversion while a true scalar does not.
A pseudoscalar, when multiplied by an ordinary vector, becomes a '' pseudovector'' ...
for the geometry. Bivectors in three dimensions are sometimes identified with pseudovector
In physics and mathematics, a pseudovector (or axial vector) is a quantity that transforms like a vector under continuous rigid transformations such as rotations or translations, but which does ''not'' transform like a vector under certain ' ...
s
to which they are related, as discussed below.
Quaternions
Bivectors are not closed under the geometric product, but the even subalgebra is. In three dimensions it consists of all scalar and bivector elements of the geometric algebra, so a general element can be written for example , where is the scalar part and is the bivector part. It is written and has basis . The product of two general elements of the even subalgebra is : The even subalgebra, that is the algebra consisting of scalars and bivectors, isisomorphic
In mathematics, an isomorphism is a structure-preserving mapping or morphism between two structures of the same type that can be reversed by an inverse mapping. Two mathematical structures are isomorphic if an isomorphism exists between the ...
to the quaternion
In mathematics, the quaternion number system extends the complex numbers. Quaternions were first described by the Irish mathematician William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space. The algebra of quater ...
s, . This can be seen by comparing the basis to the quaternion basis, or from the above product which is identical to the quaternion product, except for a change of sign which relates to the negative products in the bivector scalar product . Other quaternion properties can be similarly related to or derived from geometric algebra.
This suggests that the usual split of a quaternion into scalar and vector parts would be better represented as a split into scalar and bivector parts; if this is done the quaternion product is merely the geometric product. It also relates quaternions in three dimensions to complex numbers in two, as each is isomorphic to the even subalgebra for the dimension, a relationship that generalises to higher dimensions.
Rotation vector
The rotation vector, from theaxis–angle representation
In mathematics, the axis–angle representation parameterizes a rotation in a three-dimensional Euclidean space by two quantities: a unit vector indicating the direction of an axis of rotation, and an angle of rotation describing the magnitu ...
of rotations, is a compact way of representing rotations in three dimensions. In its most compact form, it consists of a vector, the product of a unit vector
In mathematics, a unit vector in a normed vector space is a Vector (mathematics and physics), vector (often a vector (geometry), spatial vector) of Norm (mathematics), length 1. A unit vector is often denoted by a lowercase letter with a circumfle ...
that is the axis of rotation
Rotation or rotational/rotary motion is the circular movement of an object around a central line, known as an ''axis of rotation''. A plane figure can rotate in either a clockwise or counterclockwise sense around a perpendicular axis intersect ...
with the (signed) angle
In Euclidean geometry, an angle can refer to a number of concepts relating to the intersection of two straight Line (geometry), lines at a Point (geometry), point. Formally, an angle is a figure lying in a Euclidean plane, plane formed by two R ...
of rotation , so that the magnitude of the overall rotation vector equals the (unsigned) rotation angle.
The quaternion associated with the rotation is
:
In geometric algebra the rotation is represented by a bivector. This can be seen in its relation to quaternions. Let be a unit bivector in the plane of rotation, and let be the angle of rotation
The angular displacement (symbol θ, , or φ) – also called angle of rotation, rotational displacement, or rotary displacement – of a physical body is the angle (in units of radians, degrees, turns, etc.) through which the body rotates (r ...
. Then the rotation bivector is . The quaternion closely corresponds to the exponential of half of the bivector . That is, the components of the quaternion correspond to the scalar and bivector parts of the following expression:
The exponential can be defined in terms of its power series
In mathematics, a power series (in one variable) is an infinite series of the form
\sum_^\infty a_n \left(x - c\right)^n = a_0 + a_1 (x - c) + a_2 (x - c)^2 + \dots
where ''a_n'' represents the coefficient of the ''n''th term and ''c'' is a co ...
, and easily evaluated using the fact that squared is .
So rotations can be represented by bivectors. Just as quaternions are elements of the geometric algebra, they are related by the exponential map in that algebra.
Rotors
The bivector generates a rotation through the exponential map. The even elements generated rotate a general vector in three dimensions in the same way as quaternions: As in two dimensions, the quantity is called arotor
ROTOR was an elaborate air defence radar system built by the British Government in the early 1950s to counter possible attack by Soviet bombers. To get it operational as quickly as possible, it was initially made up primarily of WWII-era syst ...
and written . The quantity is then , and they generate rotations as
This is identical to two dimensions, except here rotors are four-dimensional objects isomorphic to the quaternions. This can be generalised to all dimensions, with rotors, elements of the even subalgebra with unit magnitude, being generated by the exponential map from bivectors. They form a double cover over the rotation group, so the rotors and represent the same rotation.
Axial vectors
axial vector
Axial may refer to:
* one of the Anatomical terms of location#Other directional terms, anatomical directions describing relationships in an animal body
* In geometry:
:* a geometric term of location
:* an axis of rotation
* In chemistry, referring ...
. Axial vectors, or pseudovectors, are vectors with the special feature that their coordinates undergo a sign change relative to the usual vectors (also called "polar vectors") under inversion through the origin, reflection in a plane, or other orientation-reversing linear transformation. Examples include quantities like torque
In physics and mechanics, torque is the rotational analogue of linear force. It is also referred to as the moment of force (also abbreviated to moment). The symbol for torque is typically \boldsymbol\tau, the lowercase Greek letter ''tau''. Wh ...
, angular momentum
Angular momentum (sometimes called moment of momentum or rotational momentum) is the rotational analog of Momentum, linear momentum. It is an important physical quantity because it is a Conservation law, conserved quantity – the total ang ...
and vector magnetic field
A magnetic field (sometimes called B-field) is a physical field that describes the magnetic influence on moving electric charges, electric currents, and magnetic materials. A moving charge in a magnetic field experiences a force perpendicular ...
s. Quantities that would use axial vectors in vector algebra are properly represented by bivectors in geometric algebra.
More precisely, if an underlying orientation is chosen, the axial vectors are naturally identified with the usual vectors; the Hodge dual
In mathematics, the Hodge star operator or Hodge star is a linear map defined on the exterior algebra of a finite-dimensional oriented vector space endowed with a nondegenerate symmetric bilinear form. Applying the operator to an element of the ...
then gives the isomorphism between axial vectors and bivectors, so each axial vector is associated with a bivector and vice versa; that is
:
where is the Hodge star. Note that if the underlying orientation is reversed by inversion through the origin, both the identification of the axial vectors with the usual vectors and the Hodge dual change sign, but the bivectors don't budge. Alternately, using the unit pseudoscalar in , gives
:
This is easier to use as the product is just the geometric product. But it is antisymmetric because (as in two dimensions) the unit pseudoscalar squares to , so a negative is needed in one of the products.
This relationship extends to operations like the vector-valued cross product
In mathematics, the cross product or vector product (occasionally directed area product, to emphasize its geometric significance) is a binary operation on two vectors in a three-dimensional oriented Euclidean vector space (named here E), and ...
and bivector-valued exterior product, as when written as determinant
In mathematics, the determinant is a Scalar (mathematics), scalar-valued function (mathematics), function of the entries of a square matrix. The determinant of a matrix is commonly denoted , , or . Its value characterizes some properties of the ...
s they are calculated in the same way:
:
so are related by the Hodge dual:
:
Bivectors have a number of advantages over axial vectors. They better disambiguate axial and polar vectors, that is the quantities represented by them, so it is clearer which operations are allowed and what their results are. For example, the inner product of a polar vector and an axial vector resulting from the cross product in the triple product
In geometry and algebra, the triple product is a product of three 3- dimensional vectors, usually Euclidean vectors. The name "triple product" is used for two different products, the scalar-valued scalar triple product and, less often, the ve ...
should result in a pseudoscalar
In linear algebra, a pseudoscalar is a quantity that behaves like a scalar, except that it changes sign under a parity inversion while a true scalar does not.
A pseudoscalar, when multiplied by an ordinary vector, becomes a '' pseudovector'' ...
, a result which is more obvious if the calculation is framed as the exterior product of a vector and bivector. They generalise to other dimensions; in particular bivectors can be used to describe quantities like torque and angular momentum in two as well as three dimensions. Also, they closely match geometric intuition in a number of ways, as seen in the next section.
Geometric interpretation
attitude
Attitude or Attitude may refer to:
Philosophy and psychology
* Attitude (psychology), a disposition or state of mind
** Attitude change
* Propositional attitude, a mental state held towards a proposition
Science and technology
* Orientation ...
of the plane (or alternately the rotation
Rotation or rotational/rotary motion is the circular movement of an object around a central line, known as an ''axis of rotation''. A plane figure can rotate in either a clockwise or counterclockwise sense around a perpendicular axis intersect ...
or geometric orientation of the plane), is associated with the ratio of the bivector components. In particular, three basis bivectors, , and , or scalar multiples of them, are associated with the -plane, -plane and -plane respectively.
* The magnitude
Magnitude may refer to:
Mathematics
*Euclidean vector, a quantity defined by both its magnitude and its direction
*Magnitude (mathematics), the relative size of an object
*Norm (mathematics), a term for the size or length of a vector
*Order of ...
of the bivector is associated with the signed area
In mathematics, the signed area or oriented area of a region of an affine plane is its area with orientation specified by the positive or negative sign, that is "plus" () or "minus" (). More generally, the signed area of an arbitrary surface r ...
of the plane segment, regardless of its shape. It can even be represented in other ways, such as by an angular measure. But if the vectors are interpreted as lengths, the bivector is usually interpreted as an area with the same unit of measure.
* Like the direction of a vector
Vector most often refers to:
* Euclidean vector, a quantity with a magnitude and a direction
* Disease vector, an agent that carries and transmits an infectious pathogen into another living organism
Vector may also refer to:
Mathematics a ...
, a plane associated with a bivector has a direction, a direction of being swept out, or a sense of rotation in the plane in one of two values, which may correspond to clockwise and counterclockwise when viewed from viewpoint not in the plane. This is associated with a change of sign
A sign is an object, quality, event, or entity whose presence or occurrence indicates the probable presence or occurrence of something else. A natural sign bears a causal relation to its object—for instance, thunder is a sign of storm, or me ...
in the bivector, that is, if the direction is reversed, the bivector is negated. Alternately if two bivectors have the same attitude and magnitude but opposite directions then one is the negative of the other.
* If imagined as a parallelogram, with the origin for two of its edge vectors at , then signed area is the determinant
In mathematics, the determinant is a Scalar (mathematics), scalar-valued function (mathematics), function of the entries of a square matrix. The determinant of a matrix is commonly denoted , , or . Its value characterizes some properties of the ...
of the vectors' Cartesian coordinates ().
parallelogram
In Euclidean geometry, a parallelogram is a simple polygon, simple (non-list of self-intersecting polygons, self-intersecting) quadrilateral with two pairs of Parallel (geometry), parallel sides. The opposite or facing sides of a parallelogram a ...
with edges and , as shown in the diagram. One interpretation is that the area is swept out by as it moves along . The exterior product is antisymmetric, so reversing the order of and to make move along results in a bivector with the opposite direction that is the negative of the first. The plane of bivector contains both and so they are both parallel to the plane.
Bivectors and axial vectors are related as being Hodge dual
In mathematics, the Hodge star operator or Hodge star is a linear map defined on the exterior algebra of a finite-dimensional oriented vector space endowed with a nondegenerate symmetric bilinear form. Applying the operator to an element of the ...
. In a real vector space, the Hodge dual relates the blade that represents a subspace to its orthogonal complement
In the mathematical fields of linear algebra and functional analysis, the orthogonal complement of a subspace W of a vector space V equipped with a bilinear form B is the set W^\perp of all vectors in V that are orthogonal to every vector in W. I ...
, so if a bivector represents a plane then the axial vector associated with it is simply the plane's surface normal
In geometry, a normal is an object (e.g. a line, ray, or vector) that is perpendicular to a given object. For example, the normal line to a plane curve at a given point is the infinite straight line perpendicular to the tangent line to the ...
. The plane has two normal sets of vbectors, one on each side, giving the two possible orientations for the plane and bivector.
 In three dimensions, Hodge duality relates the
In three dimensions, Hodge duality relates the cross product
In mathematics, the cross product or vector product (occasionally directed area product, to emphasize its geometric significance) is a binary operation on two vectors in a three-dimensional oriented Euclidean vector space (named here E), and ...
to the exterior product
In mathematics, specifically in topology,
the interior of a subset of a topological space is the union of all subsets of that are open in .
A point that is in the interior of is an interior point of .
The interior of is the complement of ...
. It can also be used to represent physical quantities, like torque
In physics and mechanics, torque is the rotational analogue of linear force. It is also referred to as the moment of force (also abbreviated to moment). The symbol for torque is typically \boldsymbol\tau, the lowercase Greek letter ''tau''. Wh ...
and angular momentum
Angular momentum (sometimes called moment of momentum or rotational momentum) is the rotational analog of Momentum, linear momentum. It is an important physical quantity because it is a Conservation law, conserved quantity – the total ang ...
. In vector algebra they are usually represented by pseudovectors that are perpendicular to the plane of the force
In physics, a force is an influence that can cause an Physical object, object to change its velocity unless counterbalanced by other forces. In mechanics, force makes ideas like 'pushing' or 'pulling' mathematically precise. Because the Magnitu ...
, linear momentum or displacement that they are calculated from. But if a bivector is used instead, the plane is the plane of the bivector, so is a more natural way to represent the quantities and the way in which they act. Unlike the vector representation, it generalises to other dimensions.
The geometic product of two bivectors has a geometric interpretation. For non-zero bivectors and the product can be split into symmetric and antisymmetric parts as follows:
:
Like vectors these have magnitudes and , where is the angle between the planes. In three dimensions it is the same as the angle between the normal vectors dual to the planes, and it generalises to some extent in higher dimensions.
distributivity
In mathematics, the distributive property of binary operations is a generalization of the distributive law, which asserts that the equality
x \cdot (y + z) = x \cdot y + x \cdot z
is always true in elementary algebra.
For example, in elementary ...
of the exterior product:
:
This only works in three dimensions as it is the only number of dimensions in which a vector that is parallel to both bivectors must exist. In a higher number of dimensions, bivectors generally are not associated with a single plane, or if they are (simple bivectors), two bivectors may have no vector in common, and so sum to a non-simple bivector.
Four dimensions
In four dimensions, the basis elements for the space of bivectors are (, , , , , ), so a general bivector is of the form :Orthogonality
In four dimensions, the Hodge dual of a bivector is a bivector, and the space is dual to itself. Normal vectors are not unique, instead every plane is orthogonal to all the vectors in its Hodge dual space. This can be used to partition the bivectors into two 'halves', in the following way. We have three pairs of orthogonal bivectors: , and . There are four distinct ways of picking one bivector from each of the first two pairs, and once these first two are picked their sum yields the third bivector from the other pair. For example, and .Simple bivectors in 4D
In four dimensions bivectors are generated by the exterior product of vectors in , but with one important difference from and . In four dimensions not all bivectors are simple. There are bivectors such as that cannot be generated by the exterior product of two vectors. This also means they do not have a real, that is scalar, square. In this case : The element is the pseudoscalar in , distinct from the scalar, so the square is non-scalar. All bivectors in four dimensions can be generated using at most two exterior products and four vectors. The above bivector can be written as : Similarly, every bivector can be written as the sum of two simple bivectors. It is useful to choose two orthogonal bivectors for this, and this is always possible to do. Moreover, for a generic bivector the choice of simple bivectors is unique, that is, there is only one way to decompose into orthogonal bivectors; the only exception is when the two orthogonal bivectors have equal magnitudes (as in the above example): in this case the decomposition is not unique. The decomposition is always unique in the case of simple bivectors, with the added bonus that one of the orthogonal parts is zero.Rotations in R4
As in three dimensions bivectors in four dimension generate rotations through the exponential map, and all rotations can be generated this way. As in three dimensions if is a bivector then the rotor is and rotations are generated in the same way: : The rotations generated are more complex though. They can be categorised as follows:
: ''
The rotations generated are more complex though. They can be categorised as follows:
: ''simple
Simple or SIMPLE may refer to:
*Simplicity, the state or quality of being simple
Arts and entertainment
* ''Simple'' (album), by Andy Yorke, 2008, and its title track
* "Simple" (Florida Georgia Line song), 2018
* "Simple", a song by John ...
'' rotations are those that fix a plane in 4D, and rotate by an angle "about" this plane.
: ''double
Double, The Double or Dubble may refer to:
Mathematics and computing
* Multiplication by 2
* Double precision, a floating-point representation of numbers that is typically 64 bits in length
* A double number of the form x+yj, where j^2=+1
* A ...
'' rotations have only one fixed point, the origin, and rotate through two angles about two orthogonal planes. In general the angles are different and the planes are uniquely specified
: '' isoclinic'' rotations are double rotations where the angles of rotation are equal. In this case the planes about which the rotation is taking place are not unique.
These are generated by bivectors in a straightforward way. Simple rotations are generated by simple bivectors, with the fixed plane the dual or orthogonal to the plane of the bivector. The rotation can be said to take place about that plane, in the plane of the bivector. All other bivectors generate double rotations, with the two angles of the rotation equalling the magnitudes of the two simple bivectors that the non-simple bivector is composed of. Isoclinic rotations arise when these magnitudes are equal, in which case the decomposition into two simple bivectors is not unique.
Bivectors in general do not commute, but one exception is orthogonal bivectors and exponents of them. So if the bivector , where and are orthogonal simple bivectors, is used to generate a rotation it decomposes into two simple rotations that commute as follows:
:
It is always possible to do this as all bivectors can be expressed as sums of orthogonal bivectors.
Spacetime rotations
Spacetime
In physics, spacetime, also called the space-time continuum, is a mathematical model that fuses the three dimensions of space and the one dimension of time into a single four-dimensional continuum. Spacetime diagrams are useful in visualiz ...
is a mathematical model for our universe used in special relativity. It consists of three space
Space is a three-dimensional continuum containing positions and directions. In classical physics, physical space is often conceived in three linear dimensions. Modern physicists usually consider it, with time, to be part of a boundless ...
dimensions and one time
Time is the continuous progression of existence that occurs in an apparently irreversible process, irreversible succession from the past, through the present, and into the future. It is a component quantity of various measurements used to sequ ...
dimension combined into a single four-dimensional space. It is naturally described using geometric algebra and bivectors, with the Euclidean metric
In mathematics, the Euclidean distance between two points in Euclidean space is the length of the line segment between them. It can be calculated from the Cartesian coordinates of the points using the Pythagorean theorem, and therefore is oc ...
replaced by a Minkowski metric
In physics, Minkowski space (or Minkowski spacetime) () is the main mathematical description of spacetime in the absence of general_relativity, gravitation. It combines inertial space and time manifolds into a four-dimensional model.
The model ...
. That algebra is identical to that of Euclidean space, except the signature
A signature (; from , "to sign") is a depiction of someone's name, nickname, or even a simple "X" or other mark that a person writes on documents as a proof of identity and intent. Signatures are often, but not always, Handwriting, handwritt ...
is changed, so
:
(Note the order and indices above are not universal – here is the time-like dimension). The geometric algebra is , and the subspace of bivectors is .
The simple bivectors are of two types. The simple bivectors , and have negative squares and span the bivectors of the three-dimensional subspace corresponding to Euclidean space, . These bivectors generate ordinary rotations in .
The simple bivectors , and have positive squares and as planes span a space dimension and the time dimension. These also generate rotations through the exponential map, but instead of trigonometric functions, hyperbolic functions are needed, which generates a rotor as follows:
:
where is the bivector (, etc.), identified via the metric with an antisymmetric linear transformation of . These are Lorentz boost
In physics, the Lorentz transformations are a six-parameter family of linear transformations from a coordinate frame in spacetime to another frame that moves at a constant velocity relative to the former. The respective inverse transformation ...
s, expressed in a particularly compact way, using the same kind of algebra as in and .
In general all spacetime rotations are generated from bivectors through the exponential map, that is, a general rotor generated by bivector is of the form
:
The set of all rotations in spacetime form the Lorentz group
In physics and mathematics, the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical and quantum setting for all (non-gravitational) physical phenomena. The Lorentz group is named for the Dutch physi ...
, and from them most of the consequences of special relativity can be deduced. More generally this show how transformations in Euclidean space and spacetime can all be described using the same kind of algebra.
Maxwell's equations
(Note: in this section traditional 3-vectors are indicated by lines over the symbols and spacetime vector and bivectors by bold symbols, with the vectors and exceptionally in uppercase)Maxwell's equations
Maxwell's equations, or Maxwell–Heaviside equations, are a set of coupled partial differential equations that, together with the Lorentz force law, form the foundation of classical electromagnetism, classical optics, Electrical network, electr ...
are used in physics to describe the relationship between electric
Electricity is the set of physical phenomena associated with the presence and motion of matter possessing an electric charge. Electricity is related to magnetism, both being part of the phenomenon of electromagnetism, as described by Maxwel ...
and magnetic
Magnetism is the class of physical attributes that occur through a magnetic field, which allows objects to attract or repel each other. Because both electric currents and magnetic moments of elementary particles give rise to a magnetic field, m ...
fields. Normally given as four differential equations they have a particularly compact form when the fields are expressed as a spacetime bivector from . If the electric and magnetic fields in are and then the ''electromagnetic bivector'' is
:
where is again the basis vector for the time-like dimension and is the speed of light. The product yields the bivector that is Hodge dual to in three dimensions, as #Axial vectors, discussed above, while as a product of orthogonal vectors is also bivector-valued. As a whole it is the electromagnetic tensor expressed more compactly as a bivector, and is used as follows. First it is related to the 4-current , a vector quantity given by
:
where is current density and is charge density. They are related by a differential operator ∂, which is
:
The operator ∇ is a differential operator in geometric algebra, acting on the space dimensions and given by . When applied to vectors is the divergence and is the Curl (mathematics), curl but with a bivector rather than vector result, that is dual in three dimensions to the curl. For general quantity they act as grade lowering and raising differential operators. In particular if is a scalar then this operator is just the gradient, and it can be thought of as a geometric algebraic del operator.
Together these can be used to give a particularly compact form for Maxwell's equations with sources:
:
This equation, when decomposed according to geometric algebra, using geometric products which have both grade raising and grade lowering effects, is equivalent to Maxwell's four equations. It is also related to the electromagnetic four-potential, a vector given by
:
where is the vector magnetic potential and is the electric potential. It is related to the electromagnetic bivector as follows
:
using the same differential operator .
Higher dimensions
As has been suggested in earlier sections much of geometric algebra generalises well into higher dimensions. The geometric algebra for the real space is , and the subspace of bivectors is . The number of simple bivectors needed to form a general bivector rises with the dimension, so for odd it is , for even it is . So for four and five-dimensional space, five dimensions only two simple bivectors are needed but three are required for six-dimensional space, six and seven-dimensional space, seven dimensions. For example, in six dimensions with standard basis (, , , , , ) the bivector : is the sum of three simple bivectors but no less. As in four dimensions it is always possible to find orthogonal simple bivectors for this sum.Rotations in higher dimensions
As in three and four dimensions rotors are generated by the exponential map, so : is the rotor generated by bivector . Simple rotations, that take place in a plane of rotation around a fixed blade (geometry), blade of dimension are generated by simple bivectors, while other bivectors generate more complex rotations which can be described in terms of the simple bivectors they are sums of, each related to a plane of rotation. All bivectors can be expressed as the sum of orthogonal and commutative simple bivectors, so rotations can always be decomposed into a set of commutative rotations about the planes associated with these bivectors. The group of the rotors in dimensions is the spin group, . One notable feature, related to the number of simple bivectors and so rotation planes, is that in odd dimensions every rotation has a fixed axis – it is misleading to call it an axis of rotation as in higher dimensions rotations are taking place in multiple planes orthogonal to it. This is related to bivectors, as bivectors in odd dimensions decompose into the same number of bivectors as the even dimension below, so have the same number of planes, but one extra dimension. As each plane generates rotations in two dimensions in odd dimensions there must be one dimension, that is an axis, that is not being rotated. Bivectors are also related to the rotation matrix in dimensions. As in three dimensions the characteristic equation of the matrix can be solved to find the eigenvalues. In odd dimensions this has one real root, with eigenvector the fixed axis, and in even dimensions it has no real roots, so either all or all but one of the roots are complex conjugate pairs. Each pair is associated with a simple component of the bivector associated with the rotation. In particular, the log of each pair is the magnitude up to a sign, while eigenvectors generated from the roots are parallel to and so can be used to generate the bivector. In general the eigenvalues and bivectors are unique, and the set of eigenvalues gives the full decomposition into simple bivectors; if roots are repeated then the decomposition of the bivector into simple bivectors is not unique.Projective geometry
Geometric algebra can be applied to projective geometry in a straightforward way. The geometric algebra used is , the algebra of the real vector space . This is used to describe objects in the real projective space . The non-zero vectors in or are associated with points in the projective space so vectors that differ only by a scale factor, so their exterior product is zero, map to the same point. Non-zero simple bivectors in represent lines in , with bivectors differing only by a (positive or negative) scale factor representing the same line. A description of the projective geometry can be constructed in the geometric algebra using basic operations. For example, given two distinct points in represented by vectors and the line containing them is given by (or ). Two lines intersect in a point if for their bivectors and . This point is given by the vector : The operation "" is the meet, which can be defined as above in terms of the join, for non-zero . Using these operations projective geometry can be formulated in terms of geometric algebra. For example, given a third (non-zero) bivector the point lies on the line given by if and only if : So the condition for the lines given by , and to be collinear is : which in and simplifies to : where the angle brackets denote the scalar part of the geometric product. In the same way all projective space operations can be written in terms of geometric algebra, with bivectors representing general lines in projective space, so the whole geometry can be developed using geometric algebra.Tensors and matrices
As #General bivectors and matrices, noted above a bivector can be written as a skew-symmetric matrix, which through the exponential map generates a rotation matrix that describes the same rotation as the rotor, also generated by the exponential map but applied to the vector. But it is also used with other bivectors such as the angular velocity tensor and the electromagnetic tensor, respectively a 3×3 and 4×4 skew-symmetric matrix or tensor. Real bivectors in are isomorphic to skew-symmetric matrices, or alternately to antisymmetric tensors of degree 2 on . While bivectors are isomorphic to vectors (via the dual) in three dimensions they can be represented by skew-symmetric matrices in any dimension. This is useful for relating bivectors to problems described by matrices, so they can be re-cast in terms of bivectors, given a geometric interpretation, then often solved more easily or related geometrically to other bivector problems. More generally, every real geometric algebra is Classification of Clifford algebras#Classification, isomorphic to a matrix algebra. These contain bivectors as a subspace, though often in a way which is not especially useful. These matrices are mainly of interest as a way of classifying Clifford algebras.See also
* Dyadics * Multivector * Multilinear algebraNotes
General references
* * Reprinted, Dover Publications, 2005, . * * {{Linear algebra Clifford algebras, * Geometric algebra Multilinear algebra Vector calculus Tensors Planes (geometry)