Arrhenius Equation

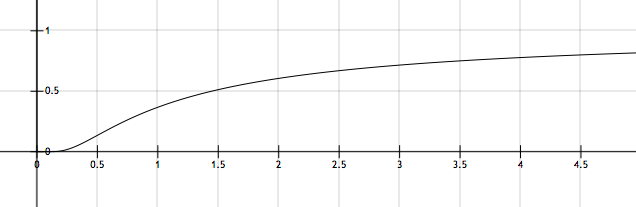In physical chemistry, the Arrhenius equation is a formula for the temperature dependence of reaction rates. The equation was proposed by Svante Arrhenius in 1889, based on the work of Dutch chemist Jacobus Henricus van 't Hoff who had noted in 1884 that the Van 't Hoff equation for the temperature dependence of equilibrium constants suggests such a formula for the rates of both forward and reverse reactions. This equation has a vast and important application in determining the rate of chemical reactions and for calculation of energy of activation. Arrhenius provided a physical justification and interpretation for the formula. Laidler, K. J. (1987) ''Chemical Kinetics'', Third Edition, Harper & Row, p. 42 Currently, it is best seen as an empirical relationship.Kenneth Connors, Chemical Kinetics, 1990, VCH Publishers It can be used to model the temperature variation of diffusion coefficients, population of crystal vacancies, creep rates, and many other thermally induced processes and reactions. The Eyring equation, developed in 1935, also expresses the relationship between rate and energy.

Formulation

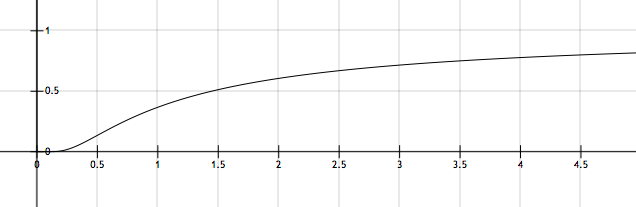The Arrhenius equation describes the exponential dependence of the rate constant of a chemical reaction on the absolute temperature as
$k = Ae^\frac,$
where
* is the rate constant (frequency of collisions resulting in a reaction),
* is the absolute temperature,
* is the pre-exponential factor or Arrhenius factor or frequency factor. Arrhenius originally considered A to be a temperature-independent constant for each chemical reaction. However more recent treatments include some temperature dependence – see ' below.
* is the molar activation energy for the reaction,
* is the universal gas constant.

Alternatively, the equation may be expressed as
$k = Ae^\frac,$
where
* is the activation energy for the reaction (in the same unit as ''k''_B''T''),
* is the Boltzmann constant.

The only difference is the unit of : the former form uses energy per mole, which is common in chemistry, while the latter form uses energy per molecule directly, which is common in physics.
The different units are accounted for in using either the gas constant, , or the Boltzmann constant, , as the multiplier of temperature .

The unit of the pre-exponential factor are identical to those of the rate constant and will vary depending on the order of the reaction. If the reaction is first order it has the unit s⁻¹, and for that reason it is often called the ''frequency factor'' or ''attempt frequency'' of the reaction. Most simply, is the number of collisions that result in a reaction per second, is the number of collisions (leading to a reaction or not) per second occurring with the proper orientation to react and $e^\frac$ is the probability that any given collision will result in a reaction. It can be seen that either increasing the temperature or decreasing the activation energy (for example through the use of catalysts) will result in an increase in rate of reaction.

Given the small temperature range of kinetic studies, it is reasonable to approximate the activation energy as being independent of the temperature. Similarly, under a wide range of practical conditions, the weak temperature dependence of the pre-exponential factor is negligible compared to the temperature dependence of the factor ; except in the case of "barrierless" diffusion-limited reactions, in which case the pre-exponential factor is dominant and is directly observable.

With this equation it can be roughly estimated that the rate of reaction increases by a factor of about 2 to 3 for every 10 °C rise in temperature, for common values of activation energy and temperature range.

The $e^$ factor denotes the fraction of molecules with energy greater than or equal to $E_a$.

Derivation

Van't Hoff argued that the temperature $T$ of a reaction and the standard equilibrium constant $k^0_\text$ exhibit the relation:

where $\Delta U^0$ denotes the apposite standard internal energy change value.

Let $k_\text$ and $k_\text$ respectively denote the forward and backward reaction rates of the reaction of interest, then
, an equation from which $\ln k^0_\text = \ln k_\text - \ln k_\text$ naturally follows.

Substituting the expression for $\ln k^0_\text$ in eq.(), we obtain .

The preceding equation can be broken down into the following two equations:

and

where $E_\text$ and $E_\text$ are the activation energies associated with the forward and backward reactions respectively, with $\Delta U^0 = E_\text - E_\text$.

Experimental findings suggest that the constants in eq.() and eq.() can be treated as being equal to zero, so that and

Integrating these equations and taking the exponential yields the results and , where each pre-exponential factor $A_\text$ or $A_\text$ is mathematically the exponential of the constant of integration for the respective indefinite integral in question.

Arrhenius plot

Taking the natural logarithm of Arrhenius equation yields:
$\ln k= \ln A - \frac \frac.$

Rearranging yields:
$\ln k = \frac\left(\frac\right) + \ln A.$

This has the same form as an equation for a straight line:
$y = a x + b,$
where ''x'' is the reciprocal of ''T''.

So, when a reaction has a rate constant obeying the Arrhenius equation, a plot of ln ''k'' versus ''T''⁻¹ gives a straight line, whose slope and intercept can be used to determine ''E''_a and ''A'' respectively. This procedure is common in experimental chemical kinetics. The activation energy is simply obtained by multiplying by (−''R'') the slope of the straight line drawn from a plot of ln ''k'' versus (1/''T''):
E_\text \equiv -R \left \frac \rightP.

Modified Arrhenius equation

The modified Arrhenius equation makes explicit the temperature dependence of the pre-exponential factor. The modified equation is usually of the form
$k = A T^n e^\frac.$

The original Arrhenius expression above corresponds to . Fitted rate constants typically lie in the range . Theoretical analyses yield various predictions for ''n''. It has been pointed out that "it is not feasible to establish, on the basis of temperature studies of the rate constant, whether the predicted ''T''^1/2 dependence of the pre-exponential factor is observed experimentally". However, if additional evidence is available, from theory and/or from experiment (such as density dependence), there is no obstacle to incisive tests of the Arrhenius law.

Another common modification is the stretched exponential form
k = A \exp \left \left(\frac\right)^\beta\right
where ''β'' is a dimensionless number of order 1. This is typically regarded as a purely empirical correction or '' fudge factor'' to make the model fit the data, but can have theoretical meaning, for example showing the presence of a range of activation energies or in special cases like the Mott variable range hopping.

Theoretical interpretation

Arrhenius's concept of activation energy

Arrhenius argued that for reactants to transform into products, they must first acquire a minimum amount of energy, called the activation energy ''E''_a. At an absolute temperature ''T'', the fraction of molecules that have a kinetic energy greater than ''E''_a can be calculated from statistical mechanics. The concept of ''activation energy'' explains the exponential nature of the relationship, and in one way or another, it is present in all kinetic theories.

The calculations for reaction rate constants involve an energy averaging over a Maxwell–Boltzmann distribution with $E_\text$ as lower bound and so are often of the type of incomplete gamma functions, which turn out to be proportional to $e^$.

Collision theory

One approach is the collision theory of chemical reactions, developed by Max Trautz and William Lewis in the years 1916–18. In this theory, molecules are supposed to react if they collide with a relative kinetic energy along their line of centers that exceeds ''E''_a. The number of binary collisions between two unlike molecules per second per unit volume is found to be
$z_ = N_\text N_\text d_^2 \sqrt\frac ,$
where ''N_A'' and ''N_B'' are the number densities of ''A'' and ''B'', ''d_AB'' is the average diameter of ''A'' and ''B'', ''T'' is the temperature which is multiplied by the Boltzmann constant ''k''_B to convert to energy, and ''μ_AB'' is the reduced mass of ''A'' and ''B''.

The rate constant is then calculated as , so that the collision theory predicts that the pre-exponential factor is equal to the collision number ''z_AB''. However for many reactions this agrees poorly with experiment, so the rate constant is written instead as . Here ''$\rho$'' is an empirical steric factor, often much less than 1.00, which is interpreted as the fraction of sufficiently energetic collisions in which the two molecules have the correct mutual orientation to react.

Transition state theory

The Eyring equation, another Arrhenius-like expression, appears in the " transition state theory" of chemical reactions, formulated by Eugene Wigner, Henry Eyring, Michael Polanyi and M. G. Evans in the 1930s. The Eyring equation can be written:
$k = \frac e^ = \frac e^e^,$
where $\Delta G^\ddagger$ is the Gibbs energy of activation, $\Delta S^\ddagger$ is the entropy of activation, $\Delta H^\ddagger$ is the enthalpy of activation, $k_\text$ is the Boltzmann constant, and $h$ is the Planck constant.

At first sight this looks like an exponential multiplied by a factor that is ''linear'' in temperature. However, free energy is itself a temperature-dependent quantity. The free energy of activation $\Delta G^\ddagger = \Delta H^\ddagger - T\Delta S^\ddagger$ is the difference of an enthalpy term and an entropy term multiplied by the absolute temperature. The pre-exponential factor depends primarily on the entropy of activation. The overall expression again takes the form of an Arrhenius exponential (of enthalpy rather than energy) multiplied by a slowly varying function of ''T''. The precise form of the temperature dependence depends upon the reaction, and can be calculated using formulas from statistical mechanics involving the partition functions of the reactants and of the activated complex.

Limitations of the idea of Arrhenius activation energy

Both the Arrhenius activation energy and the rate constant ''k'' are experimentally determined, and represent macroscopic reaction-specific parameters that are not simply related to threshold energies and the success of individual collisions at the molecular level. Consider a particular collision (an elementary reaction) between molecules A and B. The collision angle, the relative translational energy, the internal (particularly vibrational) energy will all determine the chance that the collision will produce a product molecule AB. Macroscopic measurements of ''E'' and ''k'' are the result of many individual collisions with differing collision parameters. To probe reaction rates at molecular level, experiments are conducted under near-collisional conditions and this subject is often called molecular reaction dynamics.

Another situation where the explanation of the Arrhenius equation parameters falls short is in heterogeneous catalysis, especially for reactions that show Langmuir-Hinshelwood kinetics. Clearly, molecules on surfaces do not "collide" directly, and a simple molecular cross-section does not apply here. Instead, the pre-exponential factor reflects the travel across the surface towards the active site.

There are deviations from the Arrhenius law during the glass transition in all classes of glass-forming matter. The Arrhenius law predicts that the motion of the structural units (atoms, molecules, ions, etc.) should slow down at a slower rate through the glass transition than is experimentally observed. In other words, the structural units slow down at a faster rate than is predicted by the Arrhenius law. This observation is made reasonable assuming that the units must overcome an energy barrier by means of a thermal activation energy. The thermal energy must be high enough to allow for translational motion of the units which leads to viscous flow of the material.

See also

* Accelerated aging
* Eyring equation
* Q10 (temperature coefficient)
* Van 't Hoff equation
* Clausius–Clapeyron relation
* Gibbs–Helmholtz equation
* Cherry blossom frontpredicted using the Arrhenius equation

References

Bibliography

*
*
*

External links

Carbon Dioxide solubility in Polyethylene
– Using Arrhenius equation for calculating species solubility in polymers

{{Reaction mechanisms

Chemical kinetics
Eponymous equations of physics
Statistical mechanics