|
Truncated Tetrahedra
In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 equilateral triangle faces, 12 vertices and 18 edges (of two types). It can be constructed by truncating all 4 vertices of a regular tetrahedron. Construction The truncated tetrahedron can be constructed from a regular tetrahedron by cutting all of its vertices off, a process known as truncation. The resulting polyhedron has 4 equilateral triangles and 4 regular hexagons, 18 edges, and 12 vertices. With edge length 1, the Cartesian coordinates of the 12 vertices are points \bigl( , \pm\tfrac, \pm\tfrac \bigr) that have an even number of minus signs. Properties Given the edge length a . The surface area of a truncated tetrahedron A is the sum of 4 regular hexagons and 4 equilateral triangles' area, and its volume V is: \begin A &= 7\sqrta^2 &&\approx 12.124a^2, \\ V &= \tfrac\sqrta^3 &&\approx 2.711a^3. \end The dihedral angle of a truncated tetrahedron between tria ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Archimedean Solid
The Archimedean solids are a set of thirteen convex polyhedra whose faces are regular polygon and are vertex-transitive, although they aren't face-transitive. The solids were named after Archimedes, although he did not claim credit for them. They belong to the class of uniform polyhedra, the polyhedra with regular faces and symmetric vertices. Some Archimedean solids were portrayed in the works of artists and mathematicians during the Renaissance. The elongated square gyrobicupola or ' is an extra polyhedron with regular faces and congruent vertices, but it is not generally counted as an Archimedean solid because it is not vertex-transitive. The solids The Archimedean solids have a single vertex configuration and highly symmetric properties. A vertex configuration indicates which regular polygons meet at each vertex. For instance, the configuration 3 \cdot 5 \cdot 3 \cdot 5 indicates a polyhedron in which each vertex is met by alternating two triangles and two pentagons. Highl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Point Groups In Three Dimensions
In geometry, a point group in three dimensions is an isometry group in three dimensions that leaves the origin fixed, or correspondingly, an isometry group of a sphere. It is a subgroup of the orthogonal group O(3), the group (mathematics), group of all isometry, isometries that leave the origin fixed, or correspondingly, the group of orthogonal matrix, orthogonal matrices. O(3) itself is a subgroup of the Euclidean group E(3) of all isometries. Symmetry groups of geometric objects are isometry groups. Accordingly, analysis of isometry groups is analysis of possible symmetry, symmetries. All isometries of a Bounded set, bounded (finite) 3D object have one or more common fixed points. We follow the usual convention by choosing the Origin (mathematics), origin as one of them. The symmetry group of an object is sometimes also called its full symmetry group, as opposed to its proper symmetry group, the intersection of its full symmetry group with Euclidean group#Direct and indirect is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Truncated Triakis Tetrahedron
In geometry, the truncated triakis tetrahedron is a convex polyhedron with 16 faces: four sets of three pentagons with a shared vertex, arranged in a tetrahedral arrangement, with four hexagons in the remaining gaps. The faces cannot all be regular polygons, so it is a near-miss Johnson solid. As a fullerene, it is called tetrahedral fullerene or C28 fullerene, and has been suggested as the smallest stable carbon fullerene. Chemistry This structure is a fullerene, one of two 28-vertex fullerenes. In this context, it is called ''tetrahedral fullerene'' or C28 fullerene. It has been suggested that, as an allotrope of carbon (C28), it may form the smallest stable fullerene, and experiments have found it to be stabilized by encapsulating a metal atom. Its tetrahedral symmetry and its four irregular vertices where three pentagons meet make it tetravalent, likely either to form tetravalent clusters of fullerenes or to encapsulate tetravalent atoms such as uranium. Geometry This poly ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triakis Truncated Tetrahedral Honeycomb
The triakis truncated tetrahedral honeycomb is a space-filling tessellation (or honeycomb) in Euclidean 3-space made up of triakis truncated tetrahedra. It was discovered in 1914. Voronoi tessellation It is the Voronoi tessellation of the carbon atoms in diamond, which lie in the diamond cubic crystal structure. Being composed entirely of triakis truncated tetrahedra, it is cell-transitive. Relation to quarter cubic honeycomb It can be seen as the uniform quarter cubic honeycomb where its tetrahedral In geometry, a tetrahedron (: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular Face (geometry), faces, six straight Edge (geometry), edges, and four vertex (geometry), vertices. The tet ... cells are subdivided by the center point into 4 shorter tetrahedra, and each adjoined to the adjacent truncated tetrahedral cells. : See also * Disphenoid tetrahedral honeycomb References Honeycombs (geometry) Truncated ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Honeycomb (geometry)
In geometry, a honeycomb is a ''space filling'' or ''close packing'' of polyhedron, polyhedral or higher-dimensional ''cells'', so that there are no gaps. It is an example of the more general mathematical ''tiling'' or ''tessellation'' in any number of dimensions. Its dimension can be clarified as ''n''-honeycomb for a honeycomb of ''n''-dimensional space. Honeycombs are usually constructed in ordinary Euclidean geometry, Euclidean ("flat") space. They may also be constructed in non-Euclidean geometry, non-Euclidean spaces, such as #Hyperbolic honeycombs, hyperbolic honeycombs. Any finite uniform polytope can be projected to its circumsphere to form a uniform honeycomb in spherical space. Classification There are infinitely many honeycombs, which have only been partially classified. The more regular ones have attracted the most interest, while a rich and varied assortment of others continue to be discovered. The simplest honeycombs to build are formed from stacked layers or ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tessellation
A tessellation or tiling is the covering of a surface, often a plane, using one or more geometric shapes, called ''tiles'', with no overlaps and no gaps. In mathematics, tessellation can be generalized to higher dimensions and a variety of geometries. A periodic tiling has a repeating pattern. Some special kinds include '' regular tilings'' with regular polygonal tiles all of the same shape, and '' semiregular tilings'' with regular tiles of more than one shape and with every corner identically arranged. The patterns formed by periodic tilings can be categorized into 17 wallpaper groups. A tiling that lacks a repeating pattern is called "non-periodic". An '' aperiodic tiling'' uses a small set of tile shapes that cannot form a repeating pattern (an aperiodic set of prototiles). A '' tessellation of space'', also known as a space filling or honeycomb, can be defined in the geometry of higher dimensions. A real physical tessellation is a tiling made of materials such as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Plesiohedron
In geometry, a plesiohedron is a special kind of space-filling polyhedron, defined as the Voronoi cell of a symmetric Delone set. Three-dimensional Euclidean space can be completely filled by copies of any one of these shapes, with no overlaps. The resulting honeycomb will have symmetries that take any copy of the plesiohedron to any other copy. The plesiohedra include such well-known shapes as the cube, hexagonal prism, rhombic dodecahedron, and truncated octahedron. The largest number of faces that a plesiohedron can have is 38. Definition A set S of points in Euclidean space is a Delone set if there exists a number \varepsilon>0 such that every two points of S are at least at distance \varepsilon apart from each other and such that every point of space is within distance 1/\varepsilon of at least one point in S. So S fills space, but its points never come too close to each other. For this to be true, S must be infinite. Additionally, the set S is symmetric (in the sense needed ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
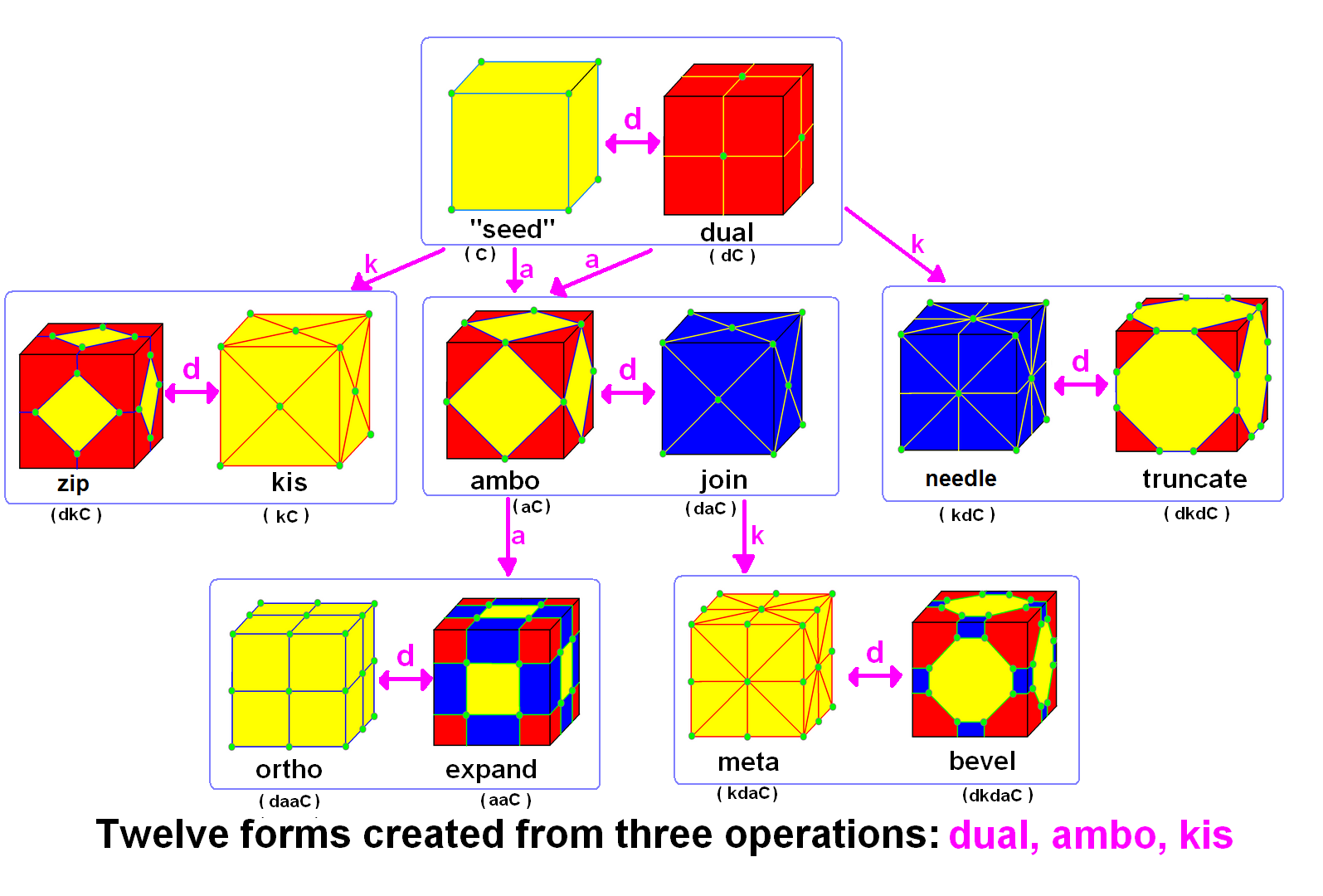
Conway Kis Operator
In geometry and topology, Conway polyhedron notation, invented by John Horton Conway and promoted by George W. Hart, is used to describe polyhedron, polyhedra based on a seed polyhedron modified by various prefix operation (mathematics), operations. Conway and Hart extended the idea of using operators, like Truncation (geometry), truncation as defined by Kepler, to build related polyhedra of the same symmetry. For example, represents a truncated cube, and , parsed as , is (topology, topologically) a truncated cuboctahedron. The simplest operator Dual polyhedron, dual swaps Vertex (geometry), vertex and Face (geometry), face elements; e.g., a dual cube is an octahedron: . Applied in a series, these operators allow many higher order polyhedra to be generated. Conway defined the operators (ambo), (bevel), (Dual polyhedron, dual), (expand), (gyro), (join), (kis), (meta), (ortho), (Snub (geometry), snub), and (Truncation (geometry), truncate), while Hart added (Reflection ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triakis Truncated Tetrahedron
In geometry, the triakis truncated tetrahedron is a convex polyhedron made from 4 hexagons and 12 isosceles triangles. It can be used to tessellate three-dimensional space, making the triakis truncated tetrahedral honeycomb. The triakis truncated tetrahedron is the shape of the Voronoi cell of the carbon atoms in diamond, which lie on the diamond cubic crystal structure. As the Voronoi cell of a symmetric space pattern, it is a plesiohedron.. Construction For space-filling, the triakis truncated tetrahedron can be constructed as follows: # Truncate a regular tetrahedron such that the big faces are regular hexagons. # Add an extra vertex at the center of each of the four smaller tetrahedra that were removed. See also *Quarter cubic honeycomb *Truncated tetrahedron *Triakis tetrahedron In geometry, a triakis tetrahedron (or tristetrahedron, or kistetrahedron) is a solid constructed by attaching four triangular pyramids onto the triangular faces of a regular tetrahedron, a Kl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triangular Cupola
In geometry, the triangular cupola is the cupola with hexagon as its base and triangle as its top. If the edges are equal in length, the triangular cupola is the Johnson solid. It can be seen as half a cuboctahedron. The triangular cupola can be applied to construct many polyhedrons. Properties The triangular cupola has 4 triangles, 3 squares, and 1 hexagon as their faces; the hexagon is the base and one of the four triangles is the top. If all of the edges are equal in length, the triangles and the hexagon becomes regular. The dihedral angle between each triangle and the hexagon is approximately 70.5°, that between each square and the hexagon is 54.7°, and that between square and triangle is 125.3°. A convex polyhedron in which all of the faces are regular is a Johnson solid, and the triangular cupola is among them, enumerated as the third Johnson solid J_ . Given that a is the edge length of a triangular cupola. Its surface area A can be calculated by adding t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Johnson Solid
In geometry, a Johnson solid, sometimes also known as a Johnson–Zalgaller solid, is a convex polyhedron whose faces are regular polygons. They are sometimes defined to exclude the uniform polyhedrons. There are ninety-two Solid geometry, solids with such a property: the first solids are the Pyramid (geometry), pyramids, Cupola (geometry), cupolas, and a Rotunda (geometry), rotunda; some of the solids may be constructed by attaching with those previous solids, whereas others may not. Definition and background A Johnson solid is a convex polyhedron whose faces are all regular polygons. The convex polyhedron means as bounded intersections of finitely many Half-space (geometry), half-spaces, or as the convex hull of finitely many points. Although there is no restriction that any given regular polygon cannot be a face of a Johnson solid, some authors required that Johnson solids are not Uniform polyhedron, uniform. This means that a Johnson solid is not a Platonic solid, Arc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Augmented Truncated Tetrahedron
In geometry, the augmented truncated tetrahedron is a polyhedron constructed by attaching a triangular cupola onto a truncated tetrahedron. It is an example of a Johnson solid. Construction The augmented truncated tetrahedron is constructed from a truncated tetrahedron by attaching a triangular cupola In geometry, the triangular cupola is the cupola with hexagon as its base and triangle as its top. If the edges are equal in length, the triangular cupola is the Johnson solid. It can be seen as half a cuboctahedron. The triangular cupola can b .... This cupola covers one of the truncated tetrahedron's four hexagonal faces, so that the resulting polyhedron's faces are eight equilateral triangles, three squares, and three regular hexagons. Since it has the property of Convex set, convexity and has regular polygonal faces, the augmented truncated tetrahedron is a Johnson solid, denoted as the sixty-fifth Johnson solid J_ . Properties The surface area of an augmented truncat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |