|
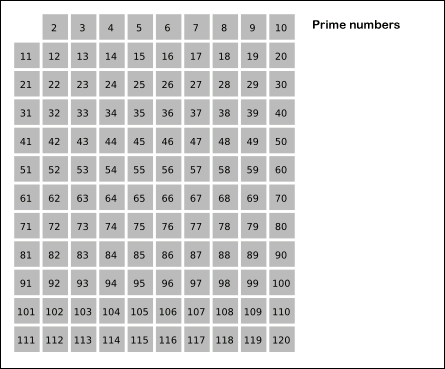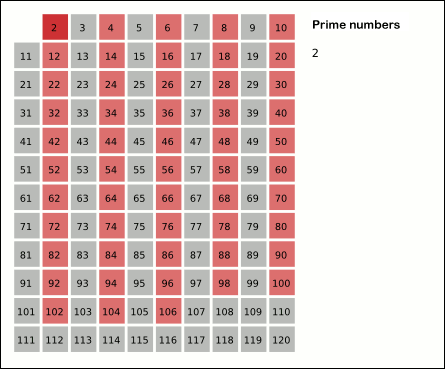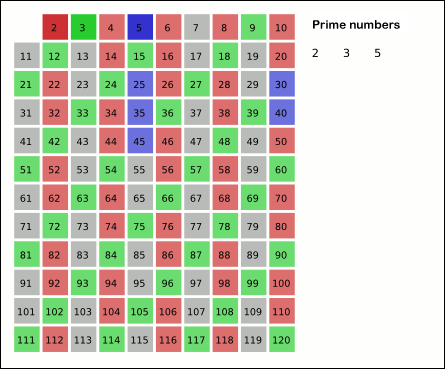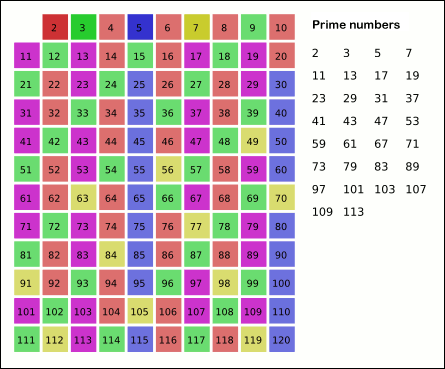
Sieve Of Atkin
In mathematics, the sieve of Atkin is a modern algorithm for finding all prime numbers up to a specified integer. Compared with the ancient sieve of Eratosthenes, which marks off multiples of primes, the sieve of Atkin does some preliminary work and then marks off multiples of ''squares'' of primes, thus achieving a better theoretical asymptotic complexity. It was created in 2003 by A. O. L. Atkin and Daniel J. Bernstein.A.O.L. Atkin, D.J. Bernstein''Prime sieves using binary quadratic forms'' Math. Comp. 73 (2004), 1023-103/ref> Algorithm In the algorithm: *All remainders are Modulo operation, modulo-sixty remainders (divide the number by 60 and return the remainder). * All numbers, including and , are positive integers. * Flipping an entry in the sieve list means to change the marking (prime or nonprime) to the opposite marking. * This results in numbers with an odd number of solutions to the corresponding equation being potentially prime (prime if they are also square fre ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
If And Only If
In logic and related fields such as mathematics and philosophy, "if and only if" (often shortened as "iff") is paraphrased by the biconditional, a logical connective between statements. The biconditional is true in two cases, where either both statements are true or both are false. The connective is biconditional (a statement of material equivalence), and can be likened to the standard material conditional ("only if", equal to "if ... then") combined with its reverse ("if"); hence the name. The result is that the truth of either one of the connected statements requires the truth of the other (i.e. either both statements are true, or both are false), though it is controversial whether the connective thus defined is properly rendered by the English "if and only if"—with its pre-existing meaning. For example, ''P if and only if Q'' means that ''P'' is true whenever ''Q'' is true, and the only case in which ''P'' is true is if ''Q'' is also true, whereas in the case of ''P if Q ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
C (programming Language)
C (''pronounced'' '' – like the letter c'') is a general-purpose programming language. It was created in the 1970s by Dennis Ritchie and remains very widely used and influential. By design, C's features cleanly reflect the capabilities of the targeted Central processing unit, CPUs. It has found lasting use in operating systems code (especially in Kernel (operating system), kernels), device drivers, and protocol stacks, but its use in application software has been decreasing. C is commonly used on computer architectures that range from the largest supercomputers to the smallest microcontrollers and embedded systems. A successor to the programming language B (programming language), B, C was originally developed at Bell Labs by Ritchie between 1972 and 1973 to construct utilities running on Unix. It was applied to re-implementing the kernel of the Unix operating system. During the 1980s, C gradually gained popularity. It has become one of the most widely used programming langu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Sieve Theory
Sieve theory is a set of general techniques in number theory, designed to count, or more realistically to estimate the size of, sifted sets of integers. The prototypical example of a sifted set is the set of prime numbers up to some prescribed limit ''X''. Correspondingly, the prototypical example of a sieve is the sieve of Eratosthenes, or the more general Legendre sieve. The direct attack on prime numbers using these methods soon reaches apparently insuperable obstacles, in the way of the accumulation of error terms. In one of the major strands of number theory in the twentieth century, ways were found of avoiding some of the difficulties of a frontal attack with a naive idea of what sieving should be. One successful approach is to approximate a specific sifted set of numbers (e.g. the set of prime numbers) by another, simpler set (e.g. the set of almost prime numbers), which is typically somewhat larger than the original set, and easier to analyze. More sophisticated sieves a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Sieve Of Sundaram
In mathematics, the sieve of Sundaram is a variant of the sieve of Eratosthenes, a simple deterministic algorithm for finding all the prime numbers up to a specified integer. It was discovered by Indian student S. P. Sundaram in 1934. Algorithm The sieve starts with a list of the integers from 1 to . From this list, all numbers of the form are removed, where and are positive integers such that and The remaining numbers are doubled and incremented by one, giving a list of the odd prime numbers (that is, all primes except 2) below The sieve of Sundaram sieves out the composite numbers just as the sieve of Eratosthenes does, but even numbers are not considered; the work of "crossing out" the multiples of 2 is done by the final double-and-increment step. Whenever Eratosthenes' method would cross out different multiples of a prime , Sundaram's method crosses out for Correctness If we start with integers from to , the final list contains only odd integers from to From ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Legendre Sieve
In mathematics, the Legendre sieve, named after Adrien-Marie Legendre, is the simplest method in modern sieve theory. It applies the concept of the Sieve of Eratosthenes to find upper or lower bounds on the number of primes within a given set of integers. Because it is a simple extension of Eratosthenes' idea, it is sometimes called the Legendre–Eratosthenes sieve.Iwaniec, HenrykThe sieve of Eratosthenes–Legendre Annali della Scuola Normale Superiore di Pisa – Classe di Scienze, Sér. 4, 4 no. 2 (1977), pp. 257–268 M453676!-- Bot generated title --> Legendre's identity The central idea of the method is expressed by the following identity, sometimes called the Legendre identity: :S(A,P)= \sum_\sum_ \mu(d) =\sum_\mu(d), A_d, , where ''A'' is a set of integers, ''P'' is a product of distinct primes, \mu is the Möbius function, and A_d is the set of integers in ''A'' divisible by ''d'', and ''S(A, P)'' is defined to be: :S(A, P) = , \, i.e. ''S''(''A'', ''P'') is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Sieve Of Eratosthenes
In mathematics, the sieve of Eratosthenes is an ancient algorithm for finding all prime numbers up to any given limit. It does so by iteratively marking as composite number, composite (i.e., not prime) the multiples of each prime, starting with the first prime number, 2. The multiples of a given prime are generated as a sequence of numbers starting from that prime, with arithmetic progression, constant difference between them that is equal to that prime.Horsley, Rev. Samuel, F. R. S., "' or, The Sieve of Eratosthenes. Being an account of his method of finding all the Prime Numbers,''Philosophical Transactions'' (1683–1775), Vol. 62. (1772), pp. 327–347 This is the sieve's key distinction from using trial division to sequentially test each candidate number for divisibility by each prime. Once all the multiples of each discovered prime have been marked as composites, the remaining unmarked numbers are primes. The earliest known reference to the sieve (, ''kóskinon Eratosthén ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Time Complexity
In theoretical computer science, the time complexity is the computational complexity that describes the amount of computer time it takes to run an algorithm. Time complexity is commonly estimated by counting the number of elementary operations performed by the algorithm, supposing that each elementary operation takes a fixed amount of time to perform. Thus, the amount of time taken and the number of elementary operations performed by the algorithm are taken to be related by a constant factor. Since an algorithm's running time may vary among different inputs of the same size, one commonly considers the worst-case time complexity, which is the maximum amount of time required for inputs of a given size. Less common, and usually specified explicitly, is the average-case complexity, which is the average of the time taken on inputs of a given size (this makes sense because there are only a finite number of possible inputs of a given size). In both cases, the time complexity is gene ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Square-free Integer
In mathematics, a square-free integer (or squarefree integer) is an integer which is divisible by no square number other than 1. That is, its prime factorization has exactly one factor for each prime that appears in it. For example, is square-free, but is not, because 18 is divisible by . The smallest positive square-free numbers are Square-free factorization Every positive integer n can be factored in a unique way as n=\prod_^k q_i^i, where the q_i different from one are square-free integers that are pairwise coprime. This is called the ''square-free factorization'' of . To construct the square-free factorization, let n=\prod_^h p_j^ be the prime factorization of n, where the p_j are distinct prime numbers. Then the factors of the square-free factorization are defined as q_i=\prod_p_j. An integer is square-free if and only if q_i=1 for all i > 1. An integer greater than one is the kth power of another integer if and only if k is a divisor of all i such that q_i\neq 1. Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Wheel Factorization
Wheel factorization is a method for generating a sequence of natural numbers by repeated additions, as determined by a number of the first few primes, so that the generated numbers are coprime with these primes, by construction. Description For a chosen number (usually no larger than 4 or 5), the first ' primes determine the specific way to generate a sequence of natural numbers which are all known in advance to be coprime with these primes; that is, they are all known to not be multiples of any of these primes. This method can thus be used for an improvement of the trial division method for integer factorization, as none of the generated numbers need be tested in trial divisions by those small primes. The trial division method consists of dividing the number to be factorized by the integers in increasing order (2, 3, 4, 5, ...) successively. A common improvement consists of testing only by primes, i.e. by 2, 3, 5, 7, 11, …. With the wheel factorization, one starts from a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Algorithm
In mathematics and computer science, an algorithm () is a finite sequence of Rigour#Mathematics, mathematically rigorous instructions, typically used to solve a class of specific Computational problem, problems or to perform a computation. Algorithms are used as specifications for performing calculations and data processing. More advanced algorithms can use Conditional (computer programming), conditionals to divert the code execution through various routes (referred to as automated decision-making) and deduce valid inferences (referred to as automated reasoning). In contrast, a Heuristic (computer science), heuristic is an approach to solving problems without well-defined correct or optimal results.David A. Grossman, Ophir Frieder, ''Information Retrieval: Algorithms and Heuristics'', 2nd edition, 2004, For example, although social media recommender systems are commonly called "algorithms", they actually rely on heuristics as there is no truly "correct" recommendation. As an e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Pseudocode
In computer science, pseudocode is a description of the steps in an algorithm using a mix of conventions of programming languages (like assignment operator, conditional operator, loop) with informal, usually self-explanatory, notation of actions and conditions. Although pseudocode shares features with regular programming languages, it is intended for human reading rather than machine control. Pseudocode typically omits details that are essential for machine implementation of the algorithm, meaning that pseudocode can only be verified by hand. The programming language is augmented with natural language description details, where convenient, or with compact mathematical notation. The reasons for using pseudocode are that it is easier for people to understand than conventional programming language code and that it is an efficient and environment-independent description of the key principles of an algorithm. It is commonly used in textbooks and scientific publications to document ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |