|
Legendre Sieve
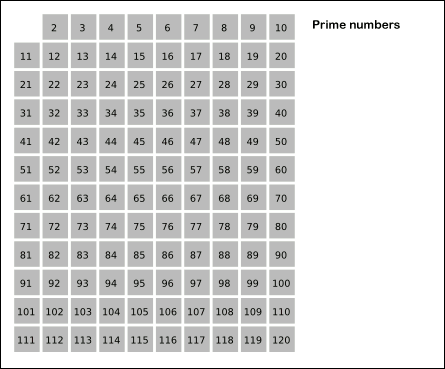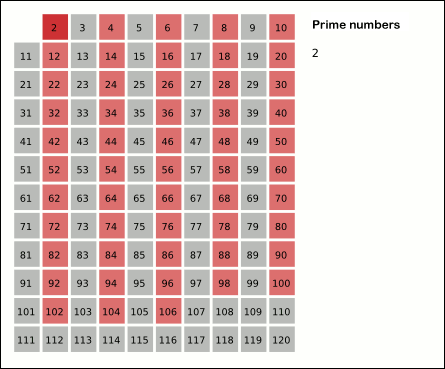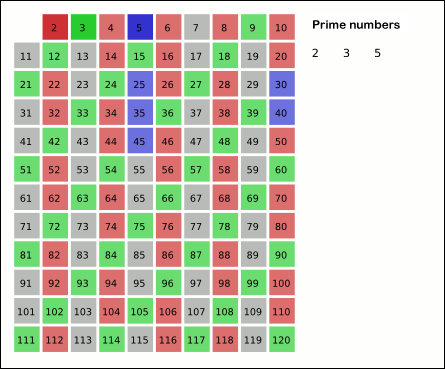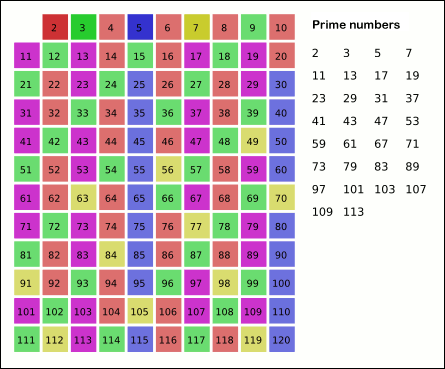
In mathematics, the Legendre sieve, named after Adrien-Marie Legendre, is the simplest method in modern sieve theory. It applies the concept of the Sieve of Eratosthenes to find upper or lower bounds on the number of primes within a given set of integers. Because it is a simple extension of Eratosthenes' idea, it is sometimes called the Legendre–Eratosthenes sieve.Iwaniec, HenrykThe sieve of Eratosthenes–Legendre Annali della Scuola Normale Superiore di Pisa – Classe di Scienze, Sér. 4, 4 no. 2 (1977), pp. 257–268 M453676!-- Bot generated title --> Legendre's identity The central idea of the method is expressed by the following identity, sometimes called the Legendre identity: :S(A,P)= \sum_\sum_ \mu(d) =\sum_\mu(d), A_d, , where ''A'' is a set of integers, ''P'' is a product of distinct primes, \mu is the Möbius function, and A_d is the set of integers in ''A'' divisible by ''d'', and ''S(A, P)'' is defined to be: :S(A, P) = , \, i.e. ''S''(''A'', ''P'') is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Adrien-Marie Legendre
Adrien-Marie Legendre (; ; 18 September 1752 – 9 January 1833) was a French people, French mathematician who made numerous contributions to mathematics. Well-known and important concepts such as the Legendre polynomials and Legendre transformation are named after him. He is also known for his contributions to the Least squares, method of least squares, and was the first to officially publish on it, though Carl Friedrich Gauss had discovered it before him. Life Adrien-Marie Legendre was born in Paris on 18 September 1752 to a wealthy family. He received his education at the Collège Mazarin in Paris, and defended his thesis in physics and mathematics in 1770. He taught at the École Militaire in Paris from 1775 to 1780 and at the École Normale Supérieure, École Normale from 1795. At the same time, he was associated with the Bureau des Longitudes. In 1782, the Prussian Academy of Sciences, Berlin Academy awarded Legendre a prize for his treatise on projectiles in resistant m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sieve Theory
Sieve theory is a set of general techniques in number theory, designed to count, or more realistically to estimate the size of, sifted sets of integers. The prototypical example of a sifted set is the set of prime numbers up to some prescribed limit ''X''. Correspondingly, the prototypical example of a sieve is the sieve of Eratosthenes, or the more general Legendre sieve. The direct attack on prime numbers using these methods soon reaches apparently insuperable obstacles, in the way of the accumulation of error terms. In one of the major strands of number theory in the twentieth century, ways were found of avoiding some of the difficulties of a frontal attack with a naive idea of what sieving should be. One successful approach is to approximate a specific sifted set of numbers (e.g. the set of prime numbers) by another, simpler set (e.g. the set of almost prime numbers), which is typically somewhat larger than the original set, and easier to analyze. More sophisticated sieves a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sieve Of Eratosthenes
In mathematics, the sieve of Eratosthenes is an ancient algorithm for finding all prime numbers up to any given limit. It does so by iteratively marking as composite number, composite (i.e., not prime) the multiples of each prime, starting with the first prime number, 2. The multiples of a given prime are generated as a sequence of numbers starting from that prime, with arithmetic progression, constant difference between them that is equal to that prime.Horsley, Rev. Samuel, F. R. S., "' or, The Sieve of Eratosthenes. Being an account of his method of finding all the Prime Numbers,''Philosophical Transactions'' (1683–1775), Vol. 62. (1772), pp. 327–347 This is the sieve's key distinction from using trial division to sequentially test each candidate number for divisibility by each prime. Once all the multiples of each discovered prime have been marked as composites, the remaining unmarked numbers are primes. The earliest known reference to the sieve (, ''kóskinon Eratosthén ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Upper Bound
In mathematics, particularly in order theory, an upper bound or majorant of a subset of some preordered set is an element of that is every element of . Dually, a lower bound or minorant of is defined to be an element of that is less than or equal to every element of . A set with an upper (respectively, lower) bound is said to be bounded from above or majorized (respectively bounded from below or minorized) by that bound. The terms bounded above (bounded below) are also used in the mathematical literature for sets that have upper (respectively lower) bounds. Examples For example, is a lower bound for the set (as a subset of the integers or of the real numbers, etc.), and so is . On the other hand, is not a lower bound for since it is not smaller than every element in . and other numbers ''x'' such that would be an upper bound for ''S''. The set has as both an upper bound and a lower bound; all other numbers are either an upper bound or a lower bound for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prime Number
A prime number (or a prime) is a natural number greater than 1 that is not a Product (mathematics), product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways of writing it as a product, or , involve 5 itself. However, 4 is composite because it is a product (2 × 2) in which both numbers are smaller than 4. Primes are central in number theory because of the fundamental theorem of arithmetic: every natural number greater than 1 is either a prime itself or can be factorization, factorized as a product of primes that is unique up to their order. The property of being prime is called primality. A simple but slow primality test, method of checking the primality of a given number , called trial division, tests whether is a multiple of any integer between 2 and . Faster algorithms include the Miller–Rabin primality test, which is fast but has a small chance of error ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eratosthenes
Eratosthenes of Cyrene (; ; – ) was an Ancient Greek polymath: a Greek mathematics, mathematician, geographer, poet, astronomer, and music theory, music theorist. He was a man of learning, becoming the chief librarian at the Library of Alexandria. His work is comparable to the study of geography, and he introduced some of the terminology, even coining the terms geography and geographer. He is best known for being the first person known to calculate the Earth's circumference, which he did by using the extensive survey results he could access in his role at the Library. His calculation was remarkably accurate (his error margin turned out to be less than 1%). He was the first to calculate Earth's axial tilt, which similarly proved to have remarkable accuracy. He created the Eratosthenes' Map of the World, first global projection of the world, incorporating Circle of latitude, parallels and Longitude, meridians based on the available geographic knowledge of his era. Eratosth ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Möbius Function
The Möbius function \mu(n) is a multiplicative function in number theory introduced by the German mathematician August Ferdinand Möbius (also transliterated ''Moebius'') in 1832. It is ubiquitous in elementary and analytic number theory and most often appears as part of its namesake the Möbius inversion formula. Following work of Gian-Carlo Rota in the 1960s, generalizations of the Möbius function were introduced into combinatorics, and are similarly denoted \mu(x). Definition The Möbius function is defined by :\mu(n) = \begin 1 & \text n = 1 \\ (-1)^k & \text n \text k \text \\ 0 & \text n \text > 1 \end The Möbius function can alternatively be represented as : \mu(n) = \delta_ \lambda(n), where \delta_ is the Kronecker delta, \lambda(n) is the Liouville function, Prime omega function, \omega(n) is the number of distinct prime divisors of n, and Prime omega function, \Omega(n) is the number of prime factors of n, counted with multiplicity. Another characterization ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Floor Function
In mathematics, the floor function is the function that takes as input a real number , and gives as output the greatest integer less than or equal to , denoted or . Similarly, the ceiling function maps to the least integer greater than or equal to , denoted or . For example, for floor: , , and for ceiling: , and . The floor of is also called the integral part, integer part, greatest integer, or entier of , and was historically denoted (among other notations). However, the same term, ''integer part'', is also used for truncation towards zero, which differs from the floor function for negative numbers. For an integer , . Although and produce graphs that appear exactly alike, they are not the same when the value of is an exact integer. For example, when , . However, if , then , while . Notation The ''integral part'' or ''integer part'' of a number ( in the original) was first defined in 1798 by Adrien-Marie Legendre in his proof of the Legendre's formula. Ca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Brun Sieve
In the field of number theory, the Brun sieve (also called Brun's pure sieve) is a technique for estimating the size of "sifted sets" of positive integers which satisfy a set of conditions which are expressed by congruences. It was developed by Viggo Brun in 1915 and later generalized to the fundamental lemma of sieve theory by others. Description In terms of sieve theory the Brun sieve is of ''combinatorial type''; that is, it derives from a careful use of the inclusion–exclusion principle. Let A be a finite set of positive integers. Let P be some set of prime numbers. For each prime p in P, let A_p denote the set of elements of A that are divisible by p. This notation can be extended to other integers d that are products of distinct primes in P. In this case, define A_d to be the intersection of the sets A_p for the prime factors p of d. Finally, define A_1 to be A itself. Let z be an arbitrary positive real number. The object of the sieve is to estimate: S(A,P,z) = ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Selberg Sieve
In number theory, the Selberg sieve is a technique for estimating the size of "sifted sets" of positive integers which satisfy a set of conditions which are expressed by congruences. It was developed by Atle Selberg in the 1940s. Description In terms of sieve theory the Selberg sieve is of ''combinatorial type'': that is, derives from a careful use of the inclusion–exclusion principle. Selberg replaced the values of the Möbius function which arise in this by a system of weights which are then optimised to fit the given problem. The result gives an ''upper bound'' for the size of the sifted set. Let A be a set of positive integers \le x and let P be a set of primes. Let A_d denote the set of elements of A divisible by d when d is a product of distinct primes from P. Further let A_1 denote A itself. Let z be a positive real number and P(z) denote the product of the primes in P which are \le z. The object of the sieve is to estimate :S(A,P,z) = \left\vert A \setminus \big ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |