|
Wheel Factorization
Wheel factorization is a method for generating a sequence of natural numbers by repeated additions, as determined by a number of the first few primes, so that the generated numbers are coprime with these primes, by construction. Description For a chosen number (usually no larger than 4 or 5), the first ' primes determine the specific way to generate a sequence of natural numbers which are all known in advance to be coprime with these primes; that is, they are all known to not be multiples of any of these primes. This method can thus be used for an improvement of the trial division method for integer factorization, as none of the generated numbers need be tested in trial divisions by those small primes. The trial division method consists of dividing the number to be factorized by the integers in increasing order (2, 3, 4, 5, ...) successively. A common improvement consists of testing only by primes, i.e. by 2, 3, 5, 7, 11, …. With the wheel factorization, one starts from a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wheel Factorization-n=30
A wheel is a rotating component (typically circular in shape) that is intended to turn on an axle bearing. The wheel is one of the key components of the wheel and axle which is one of the six simple machines. Wheels, in conjunction with axles, allow heavy objects to be moved easily facilitating movement or transportation while supporting a load, or performing labor in machines. Wheels are also used for other purposes, such as a ship's wheel, steering wheel, potter's wheel, and flywheel. Common examples can be found in transport applications. A wheel reduces friction by facilitating motion by rolling together with the use of axles. In order for a wheel to rotate, a moment must be applied to the wheel about its axis, either by gravity or by the application of another external force or torque. Terminology The English word ''wheel'' comes from the Old English word , from Proto-Germanic , from Proto-Indo-European , an extended form of the root . Cognates within Indo-European in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sieve Of Eratosthenes
In mathematics, the sieve of Eratosthenes is an ancient algorithm for finding all prime numbers up to any given limit. It does so by iteratively marking as composite number, composite (i.e., not prime) the multiples of each prime, starting with the first prime number, 2. The multiples of a given prime are generated as a sequence of numbers starting from that prime, with arithmetic progression, constant difference between them that is equal to that prime.Horsley, Rev. Samuel, F. R. S., "' or, The Sieve of Eratosthenes. Being an account of his method of finding all the Prime Numbers,''Philosophical Transactions'' (1683–1775), Vol. 62. (1772), pp. 327–347 This is the sieve's key distinction from using trial division to sequentially test each candidate number for divisibility by each prime. Once all the multiples of each discovered prime have been marked as composites, the remaining unmarked numbers are primes. The earliest known reference to the sieve (, ''kóskinon Eratosthén ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sieve Of Atkin
In mathematics, the sieve of Atkin is a modern algorithm for finding all prime numbers up to a specified integer. Compared with the ancient sieve of Eratosthenes, which marks off multiples of primes, the sieve of Atkin does some preliminary work and then marks off multiples of ''squares'' of primes, thus achieving a better theoretical asymptotic complexity. It was created in 2003 by A. O. L. Atkin and Daniel J. Bernstein.A.O.L. Atkin, D.J. Bernstein''Prime sieves using binary quadratic forms'' Math. Comp. 73 (2004), 1023-103/ref> Algorithm In the algorithm: *All remainders are Modulo operation, modulo-sixty remainders (divide the number by 60 and return the remainder). * All numbers, including and , are positive integers. * Flipping an entry in the sieve list means to change the marking (prime or nonprime) to the opposite marking. * This results in numbers with an odd number of solutions to the corresponding equation being potentially prime (prime if they are also square fre ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sieve Of Sundaram
In mathematics, the sieve of Sundaram is a variant of the sieve of Eratosthenes, a simple deterministic algorithm for finding all the prime numbers up to a specified integer. It was discovered by Indian student S. P. Sundaram in 1934. Algorithm The sieve starts with a list of the integers from 1 to . From this list, all numbers of the form are removed, where and are positive integers such that and The remaining numbers are doubled and incremented by one, giving a list of the odd prime numbers (that is, all primes except 2) below The sieve of Sundaram sieves out the composite numbers just as the sieve of Eratosthenes does, but even numbers are not considered; the work of "crossing out" the multiples of 2 is done by the final double-and-increment step. Whenever Eratosthenes' method would cross out different multiples of a prime , Sundaram's method crosses out for Correctness If we start with integers from to , the final list contains only odd integers from to From ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Oxford University Press
Oxford University Press (OUP) is the publishing house of the University of Oxford. It is the largest university press in the world. Its first book was printed in Oxford in 1478, with the Press officially granted the legal right to print books by decree in 1586. It is the second-oldest university press after Cambridge University Press, which was founded in 1534. It is a department of the University of Oxford. It is governed by a group of 15 academics, the Delegates of the Press, appointed by the Vice Chancellor, vice-chancellor of the University of Oxford. The Delegates of the Press are led by the Secretary to the Delegates, who serves as OUP's chief executive and as its major representative on other university bodies. Oxford University Press has had a similar governance structure since the 17th century. The press is located on Walton Street, Oxford, Walton Street, Oxford, opposite Somerville College, Oxford, Somerville College, in the inner suburb of Jericho, Oxford, Jericho. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
An Introduction To The Theory Of Numbers
''An Introduction to the Theory of Numbers'' is a classic textbook in the field of number theory, by G. H. Hardy and E. M. Wright. It is on the list of 173 books essential for undergraduate math libraries. The book grew out of a series of lectures by Hardy and Wright and was first published in 1938. The third edition added an elementary proof of the prime number theorem, and the sixth edition added a chapter on elliptic curves. See also * List of important publications in mathematics This is a list of publications in mathematics, organized by field. Some reasons a particular publication might be regarded as important: *Topic creator – A publication that created a new topic *Breakthrough – A publication that cha ... References * * * * * * Reviews *E. T. Bell (July 1939). "Review: G. H. Hardy and E. M. Wright, An Introduction to the Theory of Numbers", '' Bull. Amer. Math. Soc.'' 45(7): pp. 507–509 * * Citations Mathematics textbooks Number theo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euler–Mascheroni Constant
Euler's constant (sometimes called the Euler–Mascheroni constant) is a mathematical constant, usually denoted by the lowercase Greek letter gamma (), defined as the limiting difference between the harmonic series and the natural logarithm, denoted here by : \begin \gamma &= \lim_\left(-\log n + \sum_^n \frac1\right)\\ px&=\int_1^\infty\left(-\frac1x+\frac1\right)\,\mathrm dx. \end Here, represents the floor function. The numerical value of Euler's constant, to 50 decimal places, is: History The constant first appeared in a 1734 paper by the Swiss mathematician Leonhard Euler, titled ''De Progressionibus harmonicis observationes'' (Eneström Index 43), where he described it as "worthy of serious consideration". Euler initially calculated the constant's value to 6 decimal places. In 1781, he calculated it to 16 decimal places. Euler used the notations and for the constant. The Italian mathematician Lorenzo Mascheroni attempted to calculate the constant to 32 dec ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euler's Totient Function
In number theory, Euler's totient function counts the positive integers up to a given integer that are relatively prime to . It is written using the Greek letter phi as \varphi(n) or \phi(n), and may also be called Euler's phi function. In other words, it is the number of integers in the range for which the greatest common divisor is equal to 1. The integers of this form are sometimes referred to as totatives of . For example, the totatives of are the six numbers 1, 2, 4, 5, 7 and 8. They are all relatively prime to 9, but the other three numbers in this range, 3, 6, and 9 are not, since and . Therefore, . As another example, since for the only integer in the range from 1 to is 1 itself, and . Euler's totient function is a multiplicative function, meaning that if two numbers and are relatively prime, then . This function gives the order of the multiplicative group of integers modulo (the group of units of the ring \Z/n\Z). It is also used for defining the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wheel Factorization-n=6
A wheel is a rotating component (typically circular in shape) that is intended to turn on an axle bearing. The wheel is one of the key components of the wheel and axle which is one of the six simple machines. Wheels, in conjunction with axles, allow heavy objects to be moved easily facilitating movement or transportation while supporting a load, or performing labor in machines. Wheels are also used for other purposes, such as a ship's wheel, steering wheel, potter's wheel, and flywheel. Common examples can be found in transport applications. A wheel reduces friction by facilitating motion by rolling together with the use of axles. In order for a wheel to rotate, a moment must be applied to the wheel about its axis, either by gravity or by the application of another external force or torque. Terminology The English word ''wheel'' comes from the Old English word , from Proto-Germanic , from Proto-Indo-European , an extended form of the root . Cognates within Indo-European in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algorithm
In mathematics and computer science, an algorithm () is a finite sequence of Rigour#Mathematics, mathematically rigorous instructions, typically used to solve a class of specific Computational problem, problems or to perform a computation. Algorithms are used as specifications for performing calculations and data processing. More advanced algorithms can use Conditional (computer programming), conditionals to divert the code execution through various routes (referred to as automated decision-making) and deduce valid inferences (referred to as automated reasoning). In contrast, a Heuristic (computer science), heuristic is an approach to solving problems without well-defined correct or optimal results.David A. Grossman, Ophir Frieder, ''Information Retrieval: Algorithms and Heuristics'', 2nd edition, 2004, For example, although social media recommender systems are commonly called "algorithms", they actually rely on heuristics as there is no truly "correct" recommendation. As an e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
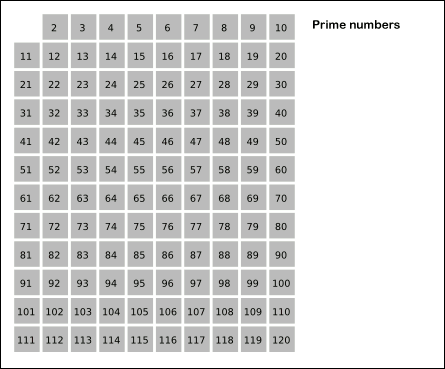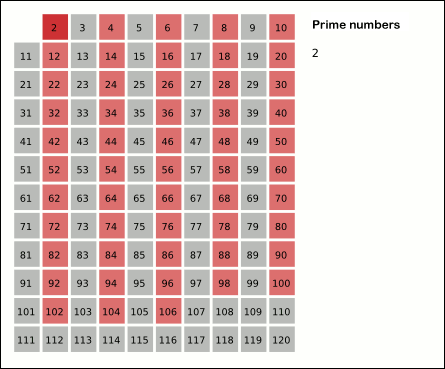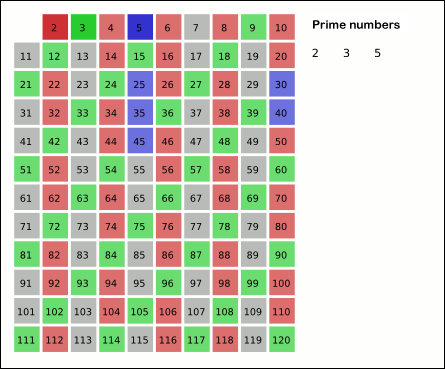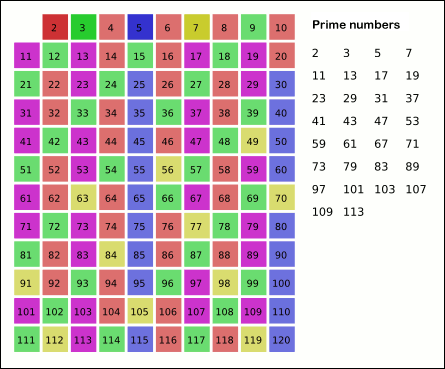
Prime Number
A prime number (or a prime) is a natural number greater than 1 that is not a Product (mathematics), product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways of writing it as a product, or , involve 5 itself. However, 4 is composite because it is a product (2 × 2) in which both numbers are smaller than 4. Primes are central in number theory because of the fundamental theorem of arithmetic: every natural number greater than 1 is either a prime itself or can be factorization, factorized as a product of primes that is unique up to their order. The property of being prime is called primality. A simple but slow primality test, method of checking the primality of a given number , called trial division, tests whether is a multiple of any integer between 2 and . Faster algorithms include the Miller–Rabin primality test, which is fast but has a small chance of error ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sieve Theory
Sieve theory is a set of general techniques in number theory, designed to count, or more realistically to estimate the size of, sifted sets of integers. The prototypical example of a sifted set is the set of prime numbers up to some prescribed limit ''X''. Correspondingly, the prototypical example of a sieve is the sieve of Eratosthenes, or the more general Legendre sieve. The direct attack on prime numbers using these methods soon reaches apparently insuperable obstacles, in the way of the accumulation of error terms. In one of the major strands of number theory in the twentieth century, ways were found of avoiding some of the difficulties of a frontal attack with a naive idea of what sieving should be. One successful approach is to approximate a specific sifted set of numbers (e.g. the set of prime numbers) by another, simpler set (e.g. the set of almost prime numbers), which is typically somewhat larger than the original set, and easier to analyze. More sophisticated sieves a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |