|
Secondary Vector Bundle Structure
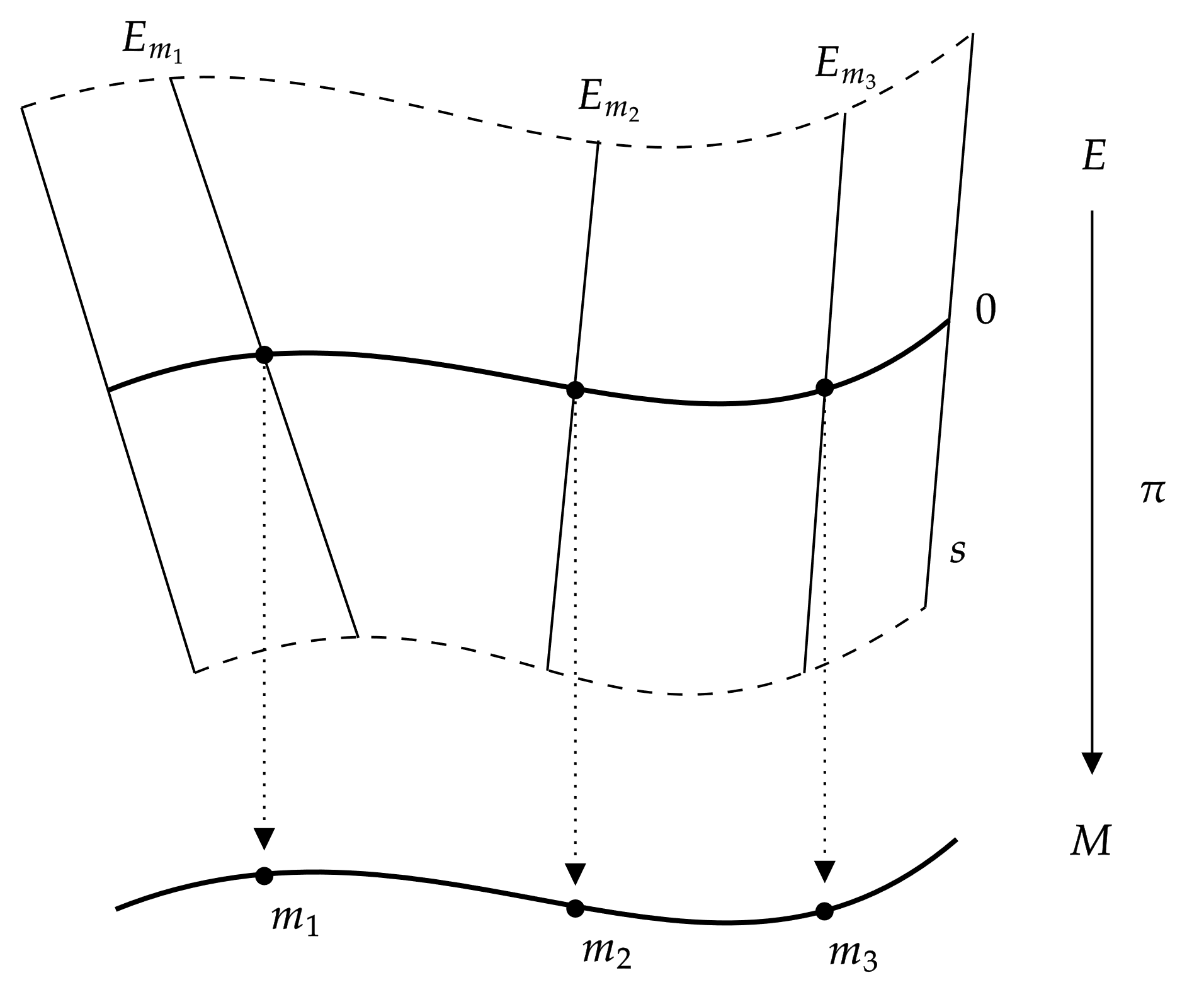
In mathematics, particularly differential topology, the secondary vector bundle structure refers to the natural vector bundle structure on the total space ''TE'' of the tangent bundle of a smooth vector bundle , induced by the push-forward of the original projection map . This gives rise to a double vector bundle structure . In the special case , where is the double tangent bundle, the secondary vector bundle is isomorphic to the tangent bundle of through the canonical flip. Construction of the secondary vector bundle structure Let be a smooth vector bundle of rank . Then the preimage of any tangent vector in in the push-forward of the canonical projection is a smooth submanifold of dimension , and it becomes a vector space with the push-forwards : +_*:T(E \times_ \! E) \to TE, \qquad \lambda_*:TE\to TE of the original addition and scalar multiplication :+:E \times_ \! E \to E, \qquad \lambda:E\to E as its vector space operations. It becomes clear +_* actuall ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Differential Topology
In mathematics, differential topology is the field dealing with the topological properties and smooth properties of smooth manifolds. In this sense differential topology is distinct from the closely related field of differential geometry, which concerns the ''geometric'' properties of smooth manifolds, including notions of size, distance, and rigid shape. By comparison differential topology is concerned with coarser properties, such as the number of holes in a manifold, its homotopy type, or the structure of its diffeomorphism group. Because many of these coarser properties may be captured algebraically, differential topology has strong links to algebraic topology. The central goal of the field of differential topology is the classification of all smooth manifolds up to diffeomorphism. Since dimension is an invariant of smooth manifolds up to diffeomorphism type, this classification is often studied by classifying the ( connected) manifolds in each dimension separately: * In ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vector Bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X (for example X could be a topological space, a manifold, or an algebraic variety): to every point x of the space X we associate (or "attach") a vector space V(x) in such a way that these vector spaces fit together to form another space of the same kind as X (e.g. a topological space, manifold, or algebraic variety), which is then called a vector bundle over X. The simplest example is the case that the family of vector spaces is constant, i.e., there is a fixed vector space V such that V(x)=V for all x in X: in this case there is a copy of V for each x in X and these copies fit together to form the vector bundle X\times V over X. Such vector bundles are said to be ''trivial''. A more complicated (and prototypical) class of examples are the tangent bundles of smooth (or differentiable) manifolds: to every point of such a mani ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tangent Bundle
A tangent bundle is the collection of all of the tangent spaces for all points on a manifold, structured in a way that it forms a new manifold itself. Formally, in differential geometry, the tangent bundle of a differentiable manifold M is a manifold TM which assembles all the tangent vectors in M . As a set, it is given by the disjoint unionThe disjoint union ensures that for any two points and of manifold the tangent spaces and have no common vector. This is graphically illustrated in the accompanying picture for tangent bundle of circle , see Examples section: all tangents to a circle lie in the plane of the circle. In order to make them disjoint it is necessary to align them in a plane perpendicular to the plane of the circle. of the tangent spaces of M . That is, : \begin TM &= \bigsqcup_ T_xM \\ &= \bigcup_ \left\ \times T_xM \\ &= \bigcup_ \left\ \\ &= \left\ \end where T_x M denotes the tangent space to M at the point x . So, an el ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pushforward (differential)
In differential geometry, pushforward is a linear approximation of smooth maps (formulating manifold) on tangent spaces. Suppose that \varphi\colon M\to N is a smooth map between smooth manifolds; then the differential of \varphi at a point x, denoted \mathrm d\varphi_x, is, in some sense, the best linear approximation of \varphi near x. It can be viewed as a generalization of the total derivative of ordinary calculus. Explicitly, the differential is a linear map from the tangent space of M at x to the tangent space of N at \varphi(x), \mathrm d\varphi_x\colon T_xM \to T_N. Hence it can be used to ''push'' tangent vectors on M ''forward'' to tangent vectors on N. The differential of a map \varphi is also called, by various authors, the derivative or total derivative of \varphi. Motivation Let \varphi: U \to V be a Smooth function#Smooth functions on and between manifolds, smooth map from an Open subset#Euclidean space, open subset U of \R^m to an open subset V of \R^n. For an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Double Vector Bundle
In mathematics, a double vector bundle is the combination of two compatible vector bundle structures, which contains in particular the tangent TE of a vector bundle E and the double tangent bundle T^2M. Definition and first consequences A double vector bundle consists of (E, E^H, E^V, B), where # the ''side bundles'' E^H and E^V are vector bundles over the base B, # E is a vector bundle on both side bundles E^H and E^V, # the projection, the addition, the scalar multiplication and the zero map on ''E'' for both vector bundle structures are morphisms. Double vector bundle morphism A double vector bundle morphism (f_E, f_H, f_V, f_B) consists of maps f_E : E \mapsto E', f_H : E^H \mapsto E^H', f_V : E^V \mapsto E^V' and f_B : B \mapsto B' such that (f_E, f_V) is a bundle morphism from (E, E^V) to (E', E^V'), (f_E, f_H) is a bundle morphism from (E, E^H) to (E', E^H'), (f_V, f_B) is a bundle morphism from (E^V, B) to (E^V', B') and (f_H, f_B) is a bundle morphism from (E^H, B) to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Double Tangent Bundle
In mathematics, particularly differential topology, the double tangent bundle or the second tangent bundle refers to the tangent bundle of the total space ''TM'' of the tangent bundle of a smooth manifold ''M'' . A note on notation: in this article, we denote projection maps by their domains, e.g., ''π''''TTM'' : ''TTM'' → ''TM''. Some authors index these maps by their ranges instead, so for them, that map would be written ''π''''TM''. The second tangent bundle arises in the study of connections and second order ordinary differential equations, i.e., (semi)spray structures on smooth manifolds, and it is not to be confused with the second order jet bundle. Secondary vector bundle structure and canonical flip Since is a vector bundle in its own right, its tangent bundle has the secondary vector bundle structure where is the push-forward of the canonical projection In the following we denote : \xi = \xi^k\frac\Big, _x\in T_xM, \qquad X = X^k\frac\Big, _x\in T_xM ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ehresmann Connection
In differential geometry, an Ehresmann connection (after the French mathematician Charles Ehresmann who first formalized this concept) is a version of the notion of a connection, which makes sense on any smooth fiber bundle. In particular, it does not rely on the possible vector bundle structure of the underlying fiber bundle, but nevertheless, linear connections may be viewed as a special case. Another important special case of Ehresmann connections are principal connections on principal bundles, which are required to be equivariant in the principal Lie group action. Introduction A covariant derivative in differential geometry is a linear differential operator which takes the directional derivative of a section of a vector bundle in a covariant manner. It also allows one to formulate a notion of a parallel section of a bundle in the direction of a vector: a section ''s'' is parallel along a vector X if \nabla_X s = 0. So a covariant derivative provides at least two things: ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Covariant Derivative
In mathematics and physics, covariance is a measure of how much two variables change together, and may refer to: Statistics * Covariance matrix, a matrix of covariances between a number of variables * Covariance or cross-covariance between two random variables or data sets * Autocovariance, the covariance of a signal with a time-shifted version of itself * Covariance function, a function giving the covariance of a random field with itself at two locations Algebra and geometry * A covariant (invariant theory) is a bihomogeneous polynomial in and the coefficients of some homogeneous form in that is invariant under some group of linear transformations. * Covariance and contravariance of vectors, properties of how vector coordinates change under a change of basis ** Covariant transformation, a rule that describes how certain physical entities change under a change of coordinate system * Covariance and contravariance of functors, properties of functors * General covariance ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Connection (vector Bundle)
In mathematics, and especially differential geometry and gauge theory, a connection on a fiber bundle is a device that defines a notion of parallel transport on the bundle; that is, a way to "connect" or identify fibers over nearby points. The most common case is that of a linear connection on a vector bundle, for which the notion of parallel transport must be linear. A linear connection is equivalently specified by a '' covariant derivative'', an operator that differentiates sections of the bundle along tangent directions in the base manifold, in such a way that parallel sections have derivative zero. Linear connections generalize, to arbitrary vector bundles, the Levi-Civita connection on the tangent bundle of a pseudo-Riemannian manifold, which gives a standard way to differentiate vector fields. Nonlinear connections generalize this concept to bundles whose fibers are not necessarily linear. Linear connections are also called Koszul connections after Jean-Louis Koszu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Double Tangent Bundle
In mathematics, particularly differential topology, the double tangent bundle or the second tangent bundle refers to the tangent bundle of the total space ''TM'' of the tangent bundle of a smooth manifold ''M'' . A note on notation: in this article, we denote projection maps by their domains, e.g., ''π''''TTM'' : ''TTM'' → ''TM''. Some authors index these maps by their ranges instead, so for them, that map would be written ''π''''TM''. The second tangent bundle arises in the study of connections and second order ordinary differential equations, i.e., (semi)spray structures on smooth manifolds, and it is not to be confused with the second order jet bundle. Secondary vector bundle structure and canonical flip Since is a vector bundle in its own right, its tangent bundle has the secondary vector bundle structure where is the push-forward of the canonical projection In the following we denote : \xi = \xi^k\frac\Big, _x\in T_xM, \qquad X = X^k\frac\Big, _x\in T_xM ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vector Bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X (for example X could be a topological space, a manifold, or an algebraic variety): to every point x of the space X we associate (or "attach") a vector space V(x) in such a way that these vector spaces fit together to form another space of the same kind as X (e.g. a topological space, manifold, or algebraic variety), which is then called a vector bundle over X. The simplest example is the case that the family of vector spaces is constant, i.e., there is a fixed vector space V such that V(x)=V for all x in X: in this case there is a copy of V for each x in X and these copies fit together to form the vector bundle X\times V over X. Such vector bundles are said to be ''trivial''. A more complicated (and prototypical) class of examples are the tangent bundles of smooth (or differentiable) manifolds: to every point of such a mani ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |