|
Offset Filtration
The offset filtration (also called the "union-of-balls" or "union-of-disks" filtration) is a growing sequence of metric balls used to detect the size and scale of topological features of a data set. The offset filtration commonly arises in persistent homology and the field of topological data analysis. Utilizing a union of balls to approximate the shape of geometric objects was first suggested by Frosini in 1992 in the context of submanifolds of Euclidean space. The construction was independently explored by Robins in 1998, and expanded to considering the collection of offsets indexed over a series of increasing scale parameters (i.e., a growing sequence of balls), in order to observe the stability of topological features with respect to attractors. Homological persistence as introduced in these papers by Frosini and Robins was subsequently formalized by Edelsbrunner et al. in their seminal 2002 paper ''Topological Persistence and Simplification.'' Since then, the offset filtration ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Offset (union-of-balls) Filtration
Offset or Off-Set may refer to: Arts, entertainment, and media * "Off-Set", a song by T.I. and Young Thug from the '' Furious 7: Original Motion Picture Soundtrack'' * ''Offset'' (EP), a 2018 EP by singer Kim Chung-ha * ''Offset'' (film), a 2006 film featuring Răzvan Vasilescu and Alexandra Maria Lara * Offset Software, a video game development company ** '' Project Offset'', working title of a first-person shooter video game by Offset Software People * Offset (rapper), a rapper and member of the American hip-hop trio Migos Science and engineering * Offset (botany), a separable part of a plant that can develop into a new, independent plant * Offset (computer science), the distance to (displacement of) an element within a data object * Offset (gears), the perpendicular distance between the axes of hypoid or offset-facing gears * Offset (geometry), see parallel curve * Offset (geophysics), the distance between a source and receiver of seismic or other geophysical readings * D ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Set
In geometry, a set of points is convex if it contains every line segment between two points in the set. For example, a solid cube (geometry), cube is a convex set, but anything that is hollow or has an indent, for example, a crescent shape, is not convex. The boundary (topology), boundary of a convex set in the plane is always a convex curve. The intersection of all the convex sets that contain a given subset of Euclidean space is called the convex hull of . It is the smallest convex set containing . A convex function is a real-valued function defined on an interval (mathematics), interval with the property that its epigraph (mathematics), epigraph (the set of points on or above the graph of a function, graph of the function) is a convex set. Convex minimization is a subfield of mathematical optimization, optimization that studies the problem of minimizing convex functions over convex sets. The branch of mathematics devoted to the study of properties of convex sets and convex f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computational Topology
Algorithmic topology, or computational topology, is a subfield of topology with an overlap with areas of computer science, in particular, computational geometry and computational complexity theory. A primary concern of algorithmic topology, as its name suggests, is to develop efficient algorithms for solving problems that arise naturally in fields such as computational geometry, graphics, robotics, social science, structural biology, and chemistry, using methods from computable topology. Major algorithms by subject area Algorithmic 3-manifold theory A large family of algorithms concerning 3-manifolds revolve around normal surface theory, which is a phrase that encompasses several techniques to turn problems in 3-manifold theory into integer linear programming problems. * ''Rubinstein and Thompson's 3-sphere recognition algorithm''. This is an algorithm that takes as input a triangulated 3-manifold and determines whether or not the manifold is homeomorphic to the 3-sphere. I ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Applied Mathematics
Applied mathematics is the application of mathematics, mathematical methods by different fields such as physics, engineering, medicine, biology, finance, business, computer science, and Industrial sector, industry. Thus, applied mathematics is a combination of mathematical science and specialized knowledge. The term "applied mathematics" also describes the profession, professional specialty in which mathematicians work on practical problems by formulating and studying mathematical models. In the past, practical applications have motivated the development of mathematical theories, which then became the subject of study in pure mathematics where abstract concepts are studied for their own sake. The activity of applied mathematics is thus intimately connected with research in pure mathematics. History Historically, applied mathematics consisted principally of Mathematical analysis, applied analysis, most notably differential equations; approximation theory (broadly construed, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
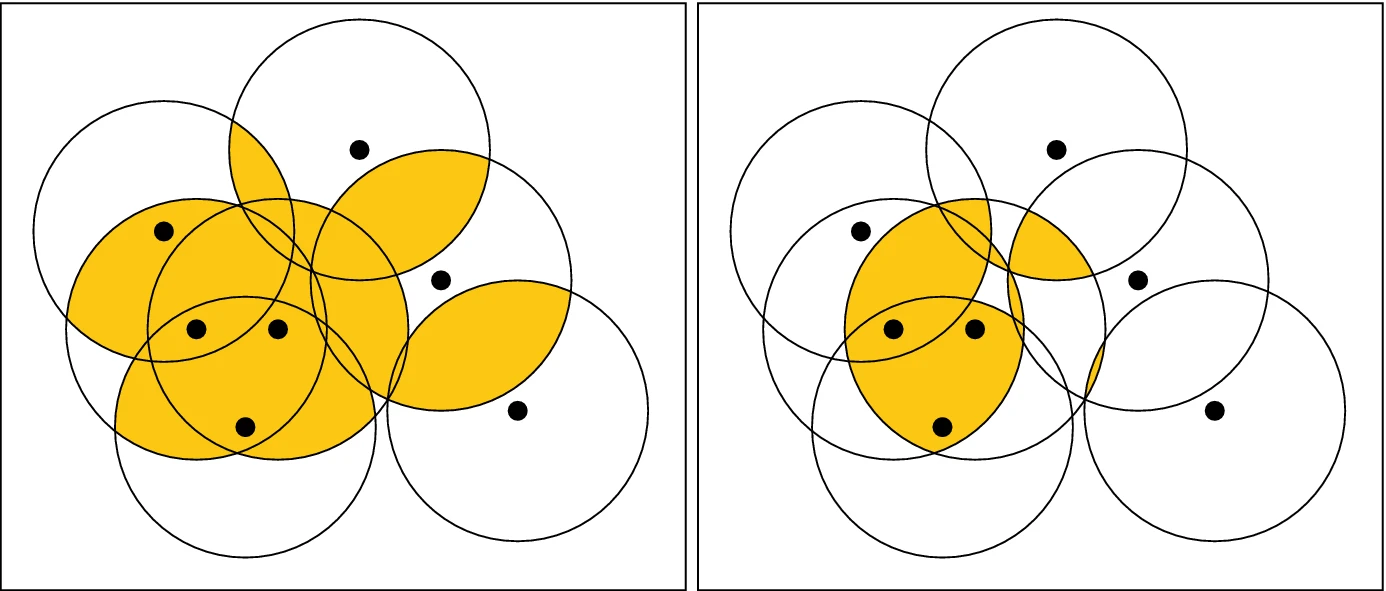
Multicover Bifiltration
The multicover bifiltration is a two-parameter sequence of nested Topological space, topological spaces derived from the covering of a finite set in a metric space by growing Ball (mathematics), metric balls. It is a multidimensional extension of the Offset Filtration, offset filtration that captures density information about the underlying data set by filtering the points of the offsets at each index according to how many balls cover each point. The multicover bifiltration has been an object of study within multidimensional persistent homology and topological data analysis. Definition Following the notation of Corbet et al. (2022), given a finite set A\subset \mathbb R^d, the multicover bifiltration on A is a two-parameter filtration indexed by \mathbb R \times \mathbb N^ defined index-wise as \operatorname_ := \, where \mathbb N denotes the non-negative integers.{{Cite journal , last1=Corbet , first1=René , last2=Kerber , first2=Michael , last3=Lesnick , first3=Michael , last4= ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |