|
Mean Longitude
Mean longitude is the ecliptic longitude at which an orbiting body could be found if its orbit were circular and free of perturbations. While nominally a simple longitude, in practice the mean longitude does not correspond to any one physical angle. Definition * Define a reference direction, ♈︎, along the ecliptic. Typically, this is the direction of the March equinox. At this point, ecliptic longitude is 0°. * The body's orbit is generally inclined to the ecliptic, therefore define the angular distance from ♈︎ to the place where the orbit crosses the ecliptic from south to north as the '' longitude of the ascending node'', . * Define the angular distance along the plane of the orbit from the ascending node to the pericenter as the '' argument of periapsis,'' . * Define the ''mean anomaly'', , as the angular distance from the periapsis which the body would have if it moved in a circular orbit, in the same orbital period as the actual body in its elliptical orbit. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ecliptic Coordinate System
In astronomy, the ecliptic coordinate system is a celestial coordinate system commonly used for representing the apparent positions, orbits, and pole orientations of Solar System objects. Because most planets (except Mercury) and many small Solar System bodies have orbits with only slight inclinations to the ecliptic, using it as the fundamental plane is convenient. The system's origin can be the center of either the Sun or Earth, its primary direction is towards the March equinox, and it has a right-hand convention. It may be implemented in spherical or rectangular coordinates. Primary direction The celestial equator and the ecliptic are slowly moving due to perturbing forces on the Earth, therefore the orientation of the primary direction, their intersection at the March equinox, is not quite fixed. A slow motion of Earth's axis, precession, causes a slow, continuous turning of the coordinate system westward about the poles of the ecliptic, completing one circ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
True Longitude
In celestial mechanics, true longitude is the ecliptic longitude at which an orbiting body could actually be found if its inclination were zero. Together with the inclination and the ascending node, the true longitude can tell us the precise direction from the central object at which the body would be located at a particular time. Calculation The true longitude can be calculated as follows: : where: * is the orbit's true anomaly In celestial mechanics, true anomaly is an angular parameter that defines the position of a body moving along a Keplerian orbit. It is the angle between the direction of periapsis and the current position of the body, as seen from the main focus ..., * is the longitude of orbit's periapsis, ** is the argument of periapsis, and ** is the longitude of the orbit's ascending node, References Orbits Equations of astronomy {{Astrophysics-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orbital Elements
Orbital elements are the parameters required to uniquely identify a specific orbit. In celestial mechanics these elements are considered in two-body systems using a Kepler orbit. There are many different ways to mathematically describe the same orbit, but certain schemes are commonly used in astronomy and orbital mechanics. A real orbit and its elements change over time due to gravitational Perturbation (astronomy), perturbations by other objects and the effects of general relativity. A Kepler orbit is an idealized, mathematical approximation of the orbit at a particular time. When viewed from an inertial frame, two orbiting bodies trace out distinct trajectories. Each of these trajectories has its Focus (geometry), focus at the common center of mass. When viewed from a non-inertial frame centered on one of the bodies, only the trajectory of the opposite body is apparent; Keplerian elements describe these non-inertial trajectories. An orbit has two sets of Keplerian elements depe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mean Motion
In orbital mechanics, mean motion (represented by ''n'') is the angular speed required for a body to complete one orbit, assuming constant speed in a circular orbit which completes in the same time as the variable speed, elliptical orbit of the actual body. The concept applies equally well to a small body revolving about a large, massive primary body or to two relatively same-sized bodies revolving about a common center of mass In physics, the center of mass of a distribution of mass in space (sometimes referred to as the barycenter or balance point) is the unique point at any given time where the weight function, weighted relative position (vector), position of the d .... While nominally a mean, and theoretically so in the case of Two-body problem, two-body motion, in practice the mean motion is not typically an average over time for the orbits of real bodies, which only approximate the two-body assumption. It is rather the instantaneous value which satisfies the above condi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orbital Elements
Orbital elements are the parameters required to uniquely identify a specific orbit. In celestial mechanics these elements are considered in two-body systems using a Kepler orbit. There are many different ways to mathematically describe the same orbit, but certain schemes are commonly used in astronomy and orbital mechanics. A real orbit and its elements change over time due to gravitational Perturbation (astronomy), perturbations by other objects and the effects of general relativity. A Kepler orbit is an idealized, mathematical approximation of the orbit at a particular time. When viewed from an inertial frame, two orbiting bodies trace out distinct trajectories. Each of these trajectories has its Focus (geometry), focus at the common center of mass. When viewed from a non-inertial frame centered on one of the bodies, only the trajectory of the opposite body is apparent; Keplerian elements describe these non-inertial trajectories. An orbit has two sets of Keplerian elements depe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mean Motion
In orbital mechanics, mean motion (represented by ''n'') is the angular speed required for a body to complete one orbit, assuming constant speed in a circular orbit which completes in the same time as the variable speed, elliptical orbit of the actual body. The concept applies equally well to a small body revolving about a large, massive primary body or to two relatively same-sized bodies revolving about a common center of mass In physics, the center of mass of a distribution of mass in space (sometimes referred to as the barycenter or balance point) is the unique point at any given time where the weight function, weighted relative position (vector), position of the d .... While nominally a mean, and theoretically so in the case of Two-body problem, two-body motion, in practice the mean motion is not typically an average over time for the orbits of real bodies, which only approximate the two-body assumption. It is rather the instantaneous value which satisfies the above condi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Epoch (astronomy)
In astronomy, an epoch or reference epoch is a instant, moment in time used as a reference point for some time-varying astronomical quantity. It is useful for the celestial coordinates or orbital elements of a Astronomical object, celestial body, as they are subject to Perturbation (astronomy), perturbations and vary with time. These time-varying astronomical quantities might include, for example, the mean longitude or mean anomaly of a body, the node of its orbit relative to a reference plane, the direction of the apogee or Perihelion and aphelion, aphelion of its orbit, or the size of the major axis of its orbit. The main use of astronomical quantities specified in this way is to calculate other relevant parameters of motion, in order to predict future positions and velocities. The applied tools of the disciplines of celestial mechanics or its subfield orbital mechanics (for predicting orbital paths and positions for bodies in motion under the gravitational effects of other bodi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Longitude Of The Periapsis
In celestial mechanics, the longitude of the periapsis, also called longitude of the pericenter, of an orbiting body is the longitude (measured from the point of the vernal equinox) at which the periapsis (closest approach to the central body) would occur if the body's orbit inclination were zero. It is usually denoted '' ϖ''. For the motion of a planet around the Sun, this position is called longitude of perihelion ϖ, which is the sum of the longitude of the ascending node Ω, and the argument of perihelion ω. The longitude of periapsis is a compound angle, with part of it being measured in the plane of reference and the rest being measured in the plane of the orbit. Likewise, any angle derived from the longitude of periapsis (e.g., mean longitude and true longitude) will also be compound. Sometimes, the term ''longitude of periapsis'' is used to refer to ''ω'', the angle between the ascending node and the periapsis. That usage of the term is especially common in discussion ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equation Of The Center
In Two-body problem, two-body, Kepler orbit, Keplerian orbital mechanics, the equation of the center is the angular difference between the actual position of a body in its elliptic orbit, elliptical orbit and the position it would occupy if its motion were uniform, in a circular orbit of the same period. It is defined as the difference true anomaly, , minus mean anomaly, , and is typically expressed a function of mean anomaly, , and orbital eccentricity, . Discussion Since antiquity, the problem of predicting the motions of the heavenly bodies has been simplified by reducing it to one of a single body in orbit about another. In calculating the position of the body around its orbit, it is often convenient to begin by assuming circular motion. This first approximation is then simply a constant angular rate multiplied by an amount of time. However, the actual solution, assuming Newtonian physics, is an elliptical orbit (a Keplerian orbit). For these, it is easy to find the mean anoma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
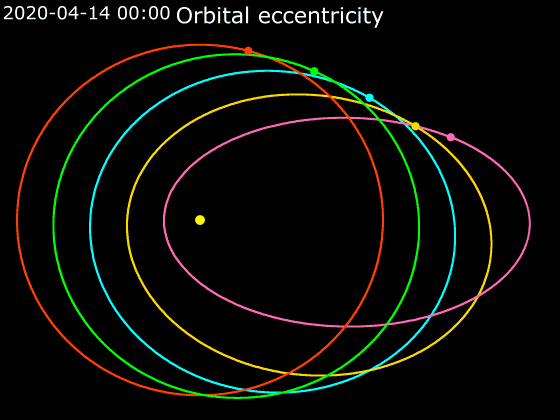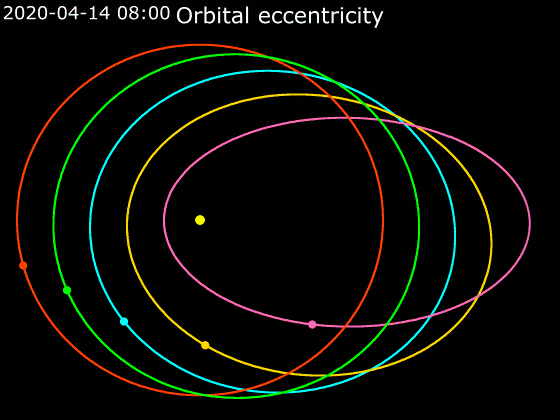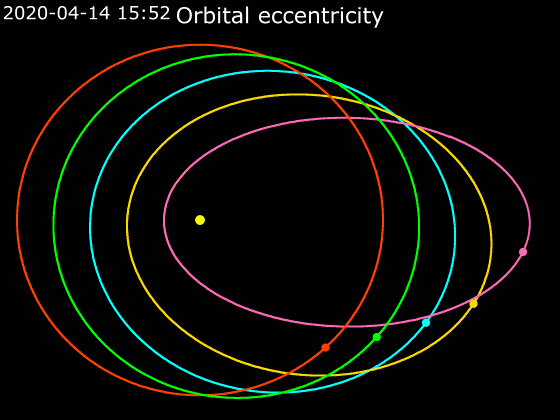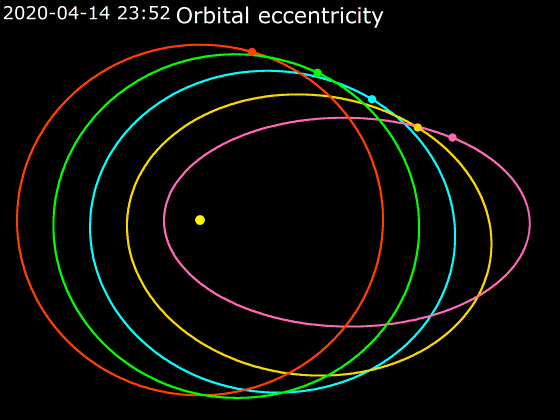
Elliptic Orbit
In astrodynamics or celestial mechanics, an elliptical orbit or eccentric orbit is an orbit with an eccentricity of less than 1; this includes the special case of a circular orbit, with eccentricity equal to 0. Some orbits have been referred to as "elongated orbits" if the eccentricity is "high" but that is not an explanatory term. For the simple two body problem, all orbits are ellipses. In a gravitational two-body problem, both bodies follow similar elliptical orbits with the same orbital period around their common barycenter. The relative position of one body with respect to the other also follows an elliptic orbit. Examples of elliptic orbits include Hohmann transfer orbits, Molniya orbits, and tundra orbits. Velocity Under standard assumptions, no other forces acting except two spherically symmetrical bodies (m_1) and (m_2), the orbital speed (v\,) of one body traveling along an elliptical orbit can be computed from the vis-viva equation as: :v = \sqrt where: * ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orbital Speed
In gravitationally bound systems, the orbital speed of an astronomical body or object (e.g. planet, moon, artificial satellite, spacecraft, or star) is the speed at which it orbits around either the barycenter (the combined center of mass) or, if one body is much more massive than the other bodies of the system combined, its speed relative to the center of mass of the most massive body. The term can be used to refer to either the mean orbital speed (i.e. the average speed over an entire orbit) or its instantaneous speed at a particular point in its orbit. The maximum (instantaneous) orbital speed occurs at periapsis (perigee, perihelion, etc.), while the minimum speed for objects in closed orbits occurs at apoapsis (apogee, aphelion, etc.). In ideal two-body systems, objects in open orbits continue to slow down forever as their distance to the barycenter increases. When a system approximates a two-body system, instantaneous orbital speed at a given point of the orbit can b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
True Anomaly
In celestial mechanics, true anomaly is an angular parameter that defines the position of a body moving along a Keplerian orbit. It is the angle between the direction of periapsis and the current position of the body, as seen from the main focus of the ellipse (the point around which the object orbits). The true anomaly is usually denoted by the Greek alphabet, Greek letters or , or the Latin script, Latin letter , and is usually restricted to the range 0–360° (0–2π rad). The true anomaly is one of three angular parameters (''anomalies'') that can be used to define a position along an orbit, the other three being the eccentric anomaly and the mean anomaly. Formulas From state vectors For elliptic orbits, the true anomaly can be calculated from orbital state vectors as: : \nu = \arccos ::(if then replace by ) where: * v is the orbital velocity vector of the orbiting body, * e is the eccentricity vector, * r is the orbital position vector (segment ''FP'' in the fi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |