|
Orbital Speed
In gravitationally bound systems, the orbital speed of an astronomical body or object (e.g. planet, moon, artificial satellite, spacecraft, or star) is the speed at which it orbits around either the barycenter (the combined center of mass) or, if one body is much more massive than the other bodies of the system combined, its speed relative to the center of mass of the most massive body. The term can be used to refer to either the mean orbital speed (i.e. the average speed over an entire orbit) or its instantaneous speed at a particular point in its orbit. The maximum (instantaneous) orbital speed occurs at periapsis (perigee, perihelion, etc.), while the minimum speed for objects in closed orbits occurs at apoapsis (apogee, aphelion, etc.). In ideal two-body systems, objects in open orbits continue to slow down forever as their distance to the barycenter increases. When a system approximates a two-body system, instantaneous orbital speed at a given point of the orbit can b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gravitational Binding Energy
The gravitational binding energy of a system is the minimum energy which must be added to it in order for the system to cease being in a gravitationally bound state. A gravitationally bound system has a lower (''i.e.'', more negative) gravitational potential energy than the sum of the energies of its parts when these are completely separated—this is what keeps the system aggregated in accordance with the minimum total potential energy principle. The gravitational binding energy can be conceptually different within the theories of Newtonian gravity and Albert Einstein's theory of gravity called General Relativity. In Newtonian gravity, the binding energy can be considered to be the linear sum of the interactions between all pairs of microscopic components of the system, while in General Relativity, this is only approximately true if the gravitational fields are all weak. When stronger fields are present within a system, the binding energy is a nonlinear property of the sy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Focus (geometry)
In geometry, focuses or foci (; : focus) are special points with reference to which any of a variety of curves is constructed. For example, one or two foci can be used in defining conic sections, the four types of which are the circle, ellipse, parabola, and hyperbola. In addition, two foci are used to define the Cassini oval and the Cartesian oval, and more than two foci are used in defining an n-ellipse, ''n''-ellipse. Conic sections Defining conics in terms of two foci An ellipse can be defined as the locus (mathematics), locus of points for which the sum of the distances to two given foci is constant. A circle is the special case of an ellipse in which the two foci coincide with each other. Thus, a circle can be more simply defined as the locus of points each of which is a fixed distance from a single given focus. A circle can also be defined as the Circles of Apollonius, circle of Apollonius, in terms of two different foci, as the locus of points having a fixed ratio of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
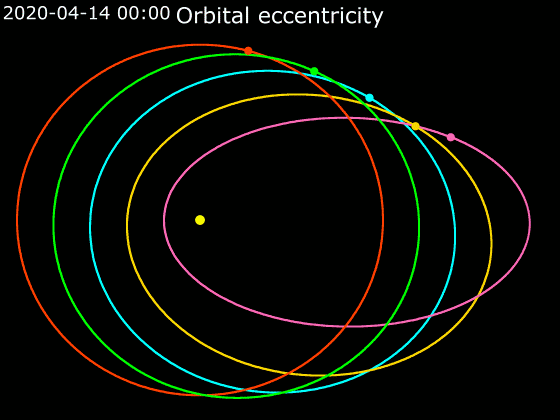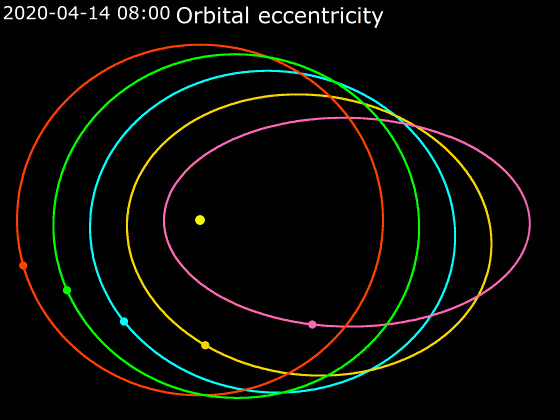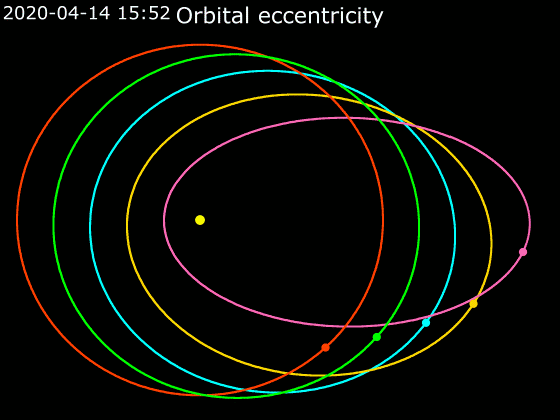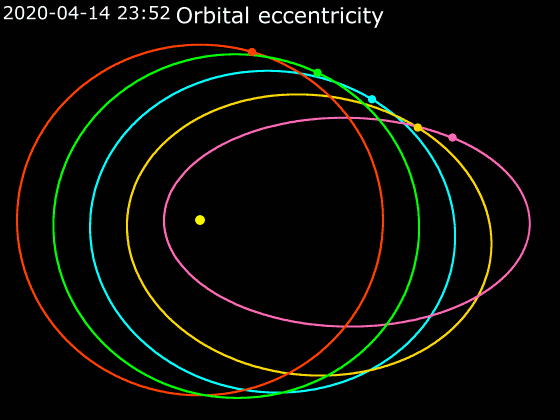
Eccentricity (orbit)
In astrodynamics, the orbital eccentricity of an astronomical object is a dimensionless parameter that determines the amount by which its orbit around another body deviates from a perfect circle. A value of 0 is a circular orbit, values between 0 and 1 form an elliptic orbit, 1 is a parabolic escape orbit (or capture orbit), and greater than 1 is a hyperbola. The term derives its name from the parameters of conic sections, as every Kepler orbit is a conic section. It is normally used for the isolated two-body problem, but extensions exist for objects following a rosette orbit through the Galaxy. Definition In a two-body problem with inverse-square-law force, every orbit is a Kepler orbit. The eccentricity of this Kepler orbit is a non-negative number that defines its shape. The eccentricity may take the following values: * Circular orbit: * Elliptic orbit: * Parabolic trajectory: * Hyperbolic trajectory: The eccentricity is given by e = \sqrt where is the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Periapsis
An apsis (; ) is the farthest or nearest point in the orbit of a planetary body about its primary body. The line of apsides (also called apse line, or major axis of the orbit) is the line connecting the two extreme values. Apsides pertaining to orbits around different bodies have distinct names to differentiate themselves from other apsides. Apsides pertaining to geocentric orbits, orbits around the Earth, are at the farthest point called the ''apogee'', and at the nearest point the ''perigee'', like with orbits of satellites and the Moon around Earth. Apsides pertaining to orbits around the Sun are named ''aphelion'' for the farthest and ''perihelion'' for the nearest point in a heliocentric orbit. Earth's two apsides are the farthest point, ''aphelion'', and the nearest point, ''perihelion'', of its orbit around the host Sun. The terms ''aphelion'' and ''perihelion'' apply in the same way to the orbits of Jupiter and the other planets, the comets, and the asteroids of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kepler's Laws Of Planetary Motion
In astronomy, Kepler's laws of planetary motion, published by Johannes Kepler in 1609 (except the third law, which was fully published in 1619), describe the orbits of planets around the Sun. These laws replaced circular orbits and epicycles in the heliocentric theory of Nicolaus Copernicus with elliptical orbits and explained how planetary velocities vary. The three laws state that: # The orbit of a planet is an ellipse with the Sun at one of the two foci. # A line segment joining a planet and the Sun sweeps out equal areas during equal intervals of time. # The square of a planet's orbital period is proportional to the cube of the length of the semi-major axis of its orbit. The elliptical orbits of planets were indicated by calculations of the orbit of Mars. From this, Kepler inferred that other bodies in the Solar System, including those farther away from the Sun, also have elliptical orbits. The second law establishes that when a planet is closer to the Sun, it travels fa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Johannes Kepler
Johannes Kepler (27 December 1571 – 15 November 1630) was a German astronomer, mathematician, astrologer, Natural philosophy, natural philosopher and writer on music. He is a key figure in the 17th-century Scientific Revolution, best known for his Kepler's laws of planetary motion, laws of planetary motion, and his books ''Astronomia nova'', ''Harmonice Mundi'', and ''Epitome Astronomiae Copernicanae'', influencing among others Isaac Newton, providing one of the foundations for his theory of Newton's law of universal gravitation, universal gravitation. The variety and impact of his work made Kepler one of the founders and fathers of modern astronomy, the scientific method, Natural science, natural and modern science. He has been described as the "father of science fiction" for his novel ''Somnium (novel), Somnium''. Kepler was a mathematics teacher at a seminary school in Graz, where he became an associate of Hans Ulrich von Eggenberg, Prince Hans Ulrich von Eggenberg. Lat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Angular Momentum
Angular momentum (sometimes called moment of momentum or rotational momentum) is the rotational analog of Momentum, linear momentum. It is an important physical quantity because it is a Conservation law, conserved quantity – the total angular momentum of a closed system remains constant. Angular momentum has both a direction (geometry), direction and a magnitude, and both are conserved. Bicycle and motorcycle dynamics, Bicycles and motorcycles, flying discs, Rifling, rifled bullets, and gyroscopes owe their useful properties to conservation of angular momentum. Conservation of angular momentum is also why hurricanes form spirals and neutron stars have high rotational rates. In general, conservation limits the possible motion of a system, but it does not uniquely determine it. The three-dimensional angular momentum for a point particle is classically represented as a pseudovector , the cross product of the particle's position vector (relative to some origin) and its mo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transverse Direction
In mathematics, the polar coordinate system specifies a given point in a plane by using a distance and an angle as its two coordinates. These are *the point's distance from a reference point called the ''pole'', and *the point's direction from the pole relative to the direction of the ''polar axis'', a ray drawn from the pole. The distance from the pole is called the ''radial coordinate'', ''radial distance'' or simply ''radius'', and the angle is called the ''angular coordinate'', ''polar angle'', or ''azimuth''. The pole is analogous to the origin in a Cartesian coordinate system. Polar coordinates are most appropriate in any context where the phenomenon being considered is inherently tied to direction and length from a center point in a plane, such as spirals. Planar physical systems with bodies moving around a central point, or phenomena originating from a central point, are often simpler and more intuitive to model using polar coordinates. The polar coordinate system is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Free-fall Time
The free-fall time is the characteristic time that would take a body to collapse under its own gravitational attraction, if no other forces existed to oppose the collapse. As such, it plays a fundamental role in setting the timescale for a wide variety of astrophysical processes—from star formation to helioseismology to supernovae—in which gravity plays a dominant role. Derivation Infall to a point source of gravity It is relatively simple to derive the free-fall time by applying Kepler's Third Law of planetary motion to a degenerate elliptic orbit. Consider a point mass m at distance R from a point source of mass M which falls radially inward to it. (Crucially, Kepler's Third Law depends only on the semi-major axis of the orbit, and does not depend on the eccentricity). A purely radial trajectory is an example of a degenerate ellipse with an eccentricity of 1 and semi-major axis R/2. Therefore, the time it would take a body to fall inward, turn around, and return to its ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Radial Elliptic Trajectory
In astrodynamics or celestial mechanics, an elliptical orbit or eccentric orbit is an orbit with an eccentricity of less than 1; this includes the special case of a circular orbit, with eccentricity equal to 0. Some orbits have been referred to as "elongated orbits" if the eccentricity is "high" but that is not an explanatory term. For the simple two body problem, all orbits are ellipses. In a gravitational two-body problem, both bodies follow similar elliptical orbits with the same orbital period around their common barycenter. The relative position of one body with respect to the other also follows an elliptic orbit. Examples of elliptic orbits include Hohmann transfer orbits, Molniya orbits, and tundra orbits. Velocity Under standard assumptions, no other forces acting except two spherically symmetrical bodies (m_1) and (m_2), the orbital speed (v\,) of one body traveling along an elliptical orbit can be computed from the vis-viva equation as: :v = \sqrt where: *\mu\ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ellipse
In mathematics, an ellipse is a plane curve surrounding two focus (geometry), focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. It generalizes a circle, which is the special type of ellipse in which the two focal points are the same. The elongation of an ellipse is measured by its eccentricity (mathematics), eccentricity e, a number ranging from e = 0 (the Limiting case (mathematics), limiting case of a circle) to e = 1 (the limiting case of infinite elongation, no longer an ellipse but a parabola). An ellipse has a simple algebraic solution for its area, but for Perimeter of an ellipse, its perimeter (also known as circumference), Integral, integration is required to obtain an exact solution. The largest and smallest diameters of an ellipse, also known as its width and height, are typically denoted and . An ellipse has four extreme points: two ''Vertex (geometry), vertices'' at the endpoints of the major axis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |