|
Cantellation
In geometry, a cantellation is a 2nd-order truncation in any dimension that bevels a regular polytope at its edges and at its vertices, creating a new facet in place of each edge and of each vertex. Cantellation also applies to regular tilings and honeycombs. Cantellating a polyhedron is also rectifying its rectification. Cantellation (for polyhedra and tilings) is also called '' expansion'' by Alicia Boole Stott: it corresponds to moving the faces of the regular form away from the center, and filling in a new face in the gap for each opened edge and for each opened vertex. Notation A cantellated polytope is represented by an extended Schläfli symbol ''t''0,2 or ''r''\beginp\\q\\...\end or ''rr''. For polyhedra, a cantellation offers a direct sequence from a regular polyhedron to its dual. Example: cantellation sequence between cube and octahedron: Example: a cuboctahedron is a cantellated tetrahedron. For higher-dimensional polytopes, a cantellation offers a direct ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Truncation (geometry)
In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new Facet (geometry), facet in place of each vertex. The term originates from Kepler's names for the Archimedean solids. Uniform truncation In general any polyhedron (or polytope) can also be truncated with a degree of freedom as to how deep the cut is, as shown in Conway polyhedron notation truncation operation. A special kind of truncation, usually implied, is a uniform truncation, a truncation operator applied to a regular polyhedron (or regular polytope) which creates a resulting uniform polyhedron (uniform polytope) with equal edge lengths. There are no degrees of freedom, and it represents a fixed geometric, just like the regular polyhedra. In general all single ringed uniform polytopes have a uniform truncation. For example, the icosidodecahedron, represented as Schläfli symbols r or \begin 5 \\ 3 \end, and Coxeter-Dynkin diagram or has a uniform truncation, the truncate ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Expansion (geometry)
In geometry, expansion is a polytope operation where Facet (mathematics), facets are separated and moved radially apart, and new facets are formed at separated elements (Vertex (geometry), vertices, Edge (geometry), edges, etc.). Equivalently this operation can be imagined by keeping facets in the same position but reducing their size. The expansion of a Regular polytope, regular convex polytope creates a uniform polytope, uniform convex polytope. For polyhedra, an expanded polyhedron has all the Face (geometry), faces of the original polyhedron, all the faces of the dual polyhedron, and new square faces in place of the original edges. Expansion of regular polytopes According to Coxeter, this multidimensional term was defined by Alicia Boole StottCoxeter, ''Regular Polytopes'' (1973), p. 123. p.210 for creating new polytopes, specifically starting from regular polytopes to construct new uniform polytopes. The ''expansion'' operation is symmetric with respect to a regular p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Small Rhombicuboctahedron
In geometry, the rhombicuboctahedron is an Archimedean solid with 26 faces, consisting of 8 equilateral triangles and 18 squares. It was named by Johannes Kepler in his 1618 Harmonices Mundi, being short for ''truncated cuboctahedral rhombus'', with cuboctahedral rhombus being his name for a rhombic dodecahedron. The rhombicuboctahedron is an Archimedean solid, and its dual is a Catalan solid, the deltoidal icositetrahedron. The elongated square gyrobicupola is a polyhedron that is similar to a rhombicuboctahedron, but it is not an Archimedean solid because it is not vertex-transitive. The rhombicuboctahedron is found in diverse cultures in architecture, toys, the arts, and elsewhere. Construction The rhombicuboctahedron may be constructed from a cube by drawing a smaller one in the middle of each face, parallel to the cube's edges. After removing the edges of a cube, the squares may be joined by adding more squares adjacent between them, and the corners may be filled by th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rectification (geometry)
In Euclidean geometry, rectification, also known as critical truncation or complete-truncation, is the process of truncating a polytope by marking the midpoints of all its edges, and cutting off its vertices at those points. The resulting polytope will be bounded by vertex figure facets and the rectified facets of the original polytope. A rectification operator is sometimes denoted by the letter with a Schläfli symbol. For example, is the rectified cube, also called a cuboctahedron, and also represented as \begin 4 \\ 3 \end. And a rectified cuboctahedron is a rhombicuboctahedron, and also represented as r\begin 4 \\ 3 \end. Conway polyhedron notation uses for ambo as this operator. In graph theory this operation creates a medial graph. The rectification of any regular self-dual polyhedron or tiling will result in another regular polyhedron or tiling with a tiling order of 4, for example the tetrahedron becoming an octahedron As a special case, a square til ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
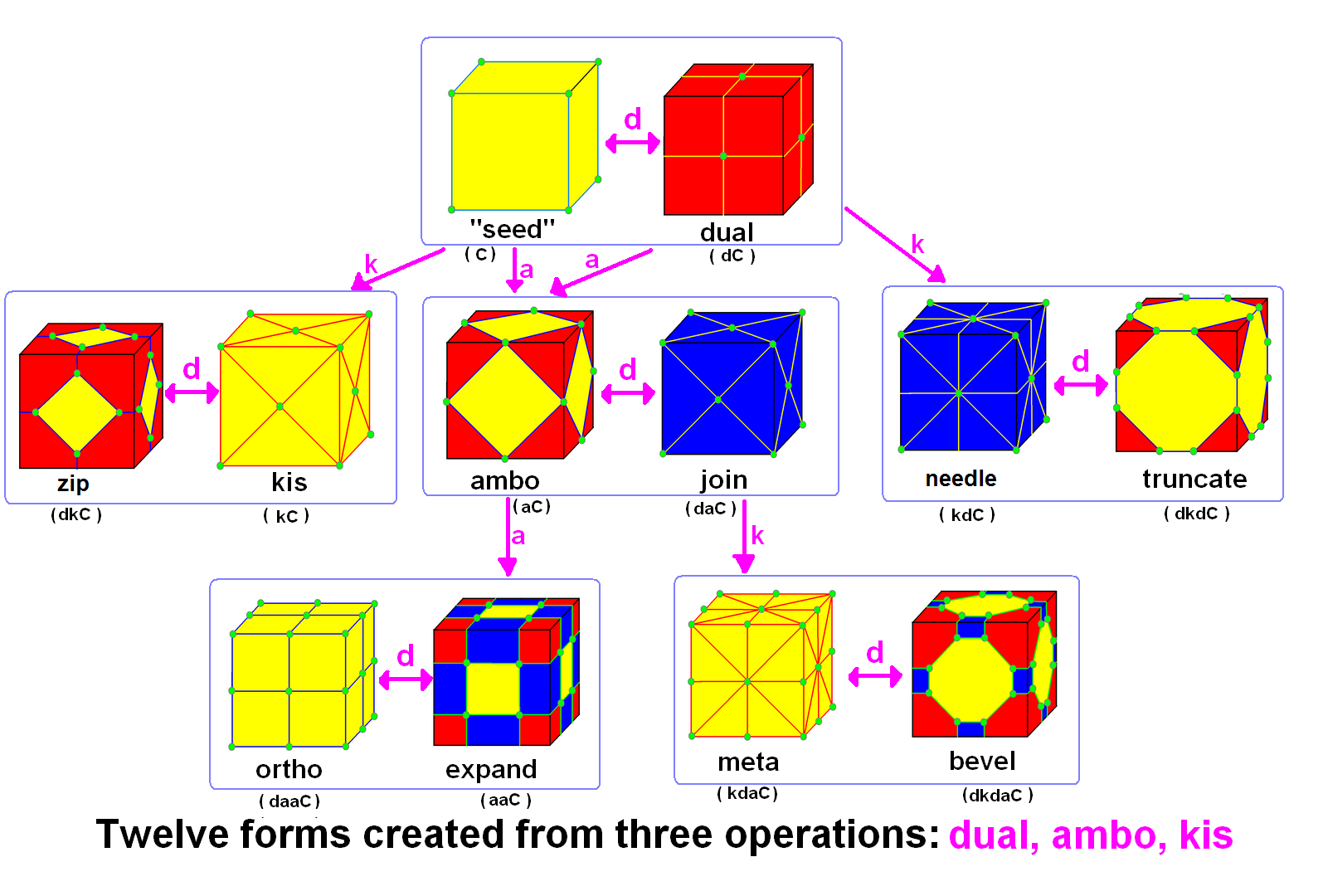
Conway Polyhedron Notation
In geometry and topology, Conway polyhedron notation, invented by John Horton Conway and promoted by George W. Hart, is used to describe polyhedra based on a seed polyhedron modified by various prefix operations. Conway and Hart extended the idea of using operators, like truncation as defined by Kepler, to build related polyhedra of the same symmetry. For example, represents a truncated cube, and , parsed as , is ( topologically) a truncated cuboctahedron. The simplest operator dual swaps vertex and face elements; e.g., a dual cube is an octahedron: . Applied in a series, these operators allow many higher order polyhedra to be generated. Conway defined the operators (ambo), (bevel), ( dual), (expand), (gyro), (join), (kis), (meta), (ortho), ( snub), and ( truncate), while Hart added ( reflect) and (propellor). Later implementations named further operators, sometimes referred to as "extended" operators. Conway's basic operations are sufficient to generate the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cuboctahedron
A cuboctahedron is a polyhedron with 8 triangular faces and 6 square faces. A cuboctahedron has 12 identical vertex (geometry), vertices, with 2 triangles and 2 squares meeting at each, and 24 identical edge (geometry), edges, each separating a triangle from a square. As such, it is a quasiregular polyhedron, i.e., an Archimedean solid that is not only vertex-transitive but also edge-transitive. It is Cuboctahedron#Radial equilateral symmetry, radially equilateral. Its dual polyhedron is the rhombic dodecahedron. Construction The cuboctahedron can be constructed in many ways: * Its construction can be started by attaching two regular triangular cupolas base-to-base. This is similar to one of the Johnson solids, triangular orthobicupola. The difference is that the triangular orthobicupola is constructed with one of the cupolas twisted so that similar polygonal faces are adjacent, whereas the cuboctahedron is not. As a result, the cuboctahedron may also called the ''triangular gyro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Icosahedron
In geometry, an icosahedron ( or ) is a polyhedron with 20 faces. The name comes . The plural can be either "icosahedra" () or "icosahedrons". There are infinitely many non- similar shapes of icosahedra, some of them being more symmetrical than others. The best known is the ( convex, non- stellated) regular icosahedron—one of the Platonic solids—whose faces are 20 equilateral triangles. Regular icosahedra There are two objects, one convex and one nonconvex, that can both be called regular icosahedra. Each has 30 edges and 20 equilateral triangle faces with five meeting at each of its twelve vertices. Both have icosahedral symmetry. The term "regular icosahedron" generally refers to the convex variety, while the nonconvex form is called a ''great icosahedron''. Convex regular icosahedron The convex regular icosahedron is usually referred to simply as the ''regular icosahedron'', one of the five regular Platonic solids, and is represented by its Schläfli symbol , contai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cube Cantellation Sequence
A cube or regular hexahedron is a three-dimensional solid object in geometry, which is bounded by six congruent square faces, a type of polyhedron. It has twelve congruent edges and eight vertices. It is a type of parallelepiped, with pairs of parallel opposite faces, and more specifically a rhombohedron, with congruent edges, and a rectangular cuboid, with right angles between pairs of intersecting faces and pairs of intersecting edges. It is an example of many classes of polyhedra: Platonic solid, regular polyhedron, parallelohedron, zonohedron, and plesiohedron. The dual polyhedron of a cube is the regular octahedron. The cube can be represented in many ways, one of which is the graph known as the cubical graph. It can be constructed by using the Cartesian product of graphs. The cube is the three-dimensional hypercube, a family of polytopes also including the two-dimensional square and four-dimensional tesseract. A cube with unit side length is the canonical unit of volume in t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cube
A cube or regular hexahedron is a three-dimensional space, three-dimensional solid object in geometry, which is bounded by six congruent square (geometry), square faces, a type of polyhedron. It has twelve congruent edges and eight vertices. It is a type of parallelepiped, with pairs of parallel opposite faces, and more specifically a rhombohedron, with congruent edges, and a rectangular cuboid, with right angles between pairs of intersecting faces and pairs of intersecting edges. It is an example of many classes of polyhedra: Platonic solid, regular polyhedron, parallelohedron, zonohedron, and plesiohedron. The dual polyhedron of a cube is the regular octahedron. The cube can be represented in many ways, one of which is the graph known as the cubical graph. It can be constructed by using the Cartesian product of graphs. The cube is the three-dimensional hypercube, a family of polytopes also including the two-dimensional square and four-dimensional tesseract. A cube with 1, unit s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tetrahedron
In geometry, a tetrahedron (: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular Face (geometry), faces, six straight Edge (geometry), edges, and four vertex (geometry), vertices. The tetrahedron is the simplest of all the ordinary convex polytope, convex polyhedra. The tetrahedron is the three-dimensional case of the more general concept of a Euclidean geometry, Euclidean simplex, and may thus also be called a 3-simplex. The tetrahedron is one kind of pyramid (geometry), pyramid, which is a polyhedron with a flat polygon base and triangular faces connecting the base to a common point. In the case of a tetrahedron, the base is a triangle (any of the four faces can be considered the base), so a tetrahedron is also known as a "triangular pyramid". Like all convex polyhedra, a tetrahedron can be folded from a single sheet of paper. It has two such net (polyhedron), nets. For any tetrahedron there exists a sphere (called th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dodecahedron
In geometry, a dodecahedron (; ) or duodecahedron is any polyhedron with twelve flat faces. The most familiar dodecahedron is the regular dodecahedron with regular pentagons as faces, which is a Platonic solid. There are also three Kepler–Poinsot polyhedron, regular star dodecahedra, which are constructed as stellations of the convex form. All of these have icosahedral symmetry, order 120. Some dodecahedra have the same combinatorial structure as the regular dodecahedron (in terms of the graph formed by its vertices and edges), but their pentagonal faces are not regular: The #Pyritohedron, pyritohedron, a common crystal form in pyrite, has pyritohedral symmetry, while the #Tetartoid, tetartoid has tetrahedral symmetry. The rhombic dodecahedron can be seen as a limiting case of the pyritohedron, and it has octahedral symmetry. The elongated dodecahedron and trapezo-rhombic dodecahedron variations, along with the rhombic dodecahedra, are space-filling polyhedra, space-filling. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |