|
Zeldovich Regularization
Zeldovich regularization refers to a regularization method to calculate divergent integrals and divergent series, that was first introduced by Yakov Zeldovich Yakov Borisovich Zeldovich (, ; 8 March 1914 – 2 December 1987), also known as YaB, was a leading Soviet people, Soviet Physics, physicist of Belarusians, Belarusian origin, who is known for his prolific contributions in physical Physical c ... in 1961. Zeldovich was originally interested in calculating the norm of the Gamow wave function which is divergent since there is an outgoing spherical wave. Zeldovich regularization uses a Gaussian type-regularization and is defined, for divergent integrals, by : \int_0^\infty f(x) dx \equiv \lim_\int_0^\infty f(x) e^ dx. and, for divergent series, byOrlov, Y. V., & Irgaziev, B. F. (2008). On the normalization of the Gamov resonant wave function in the configuration space. Bulletin of the Russian Academy of Sciences: Physics, 72, 1539-1543. :\sum_n c_n \equiv \lim_\sum_ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regularization (physics)
In physics, especially quantum field theory, regularization is a method of modifying observables which have singularities in order to make them finite by the introduction of a suitable parameter called the regulator. The regulator, also known as a "cutoff", models our lack of knowledge about physics at unobserved scales (e.g. scales of small size or large energy levels). It compensates for (and requires) the possibility of separation of scales that "new physics" may be discovered at those scales which the present theory is unable to model, while enabling the current theory to give accurate predictions as an "effective theory" within its intended scale of use. It is distinct from renormalization, another technique to control infinities without assuming new physics, by adjusting for self-interaction feedback. Regularization was for many decades controversial even amongst its inventors, as it combines physical and epistemological claims into the same equations. However, it i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
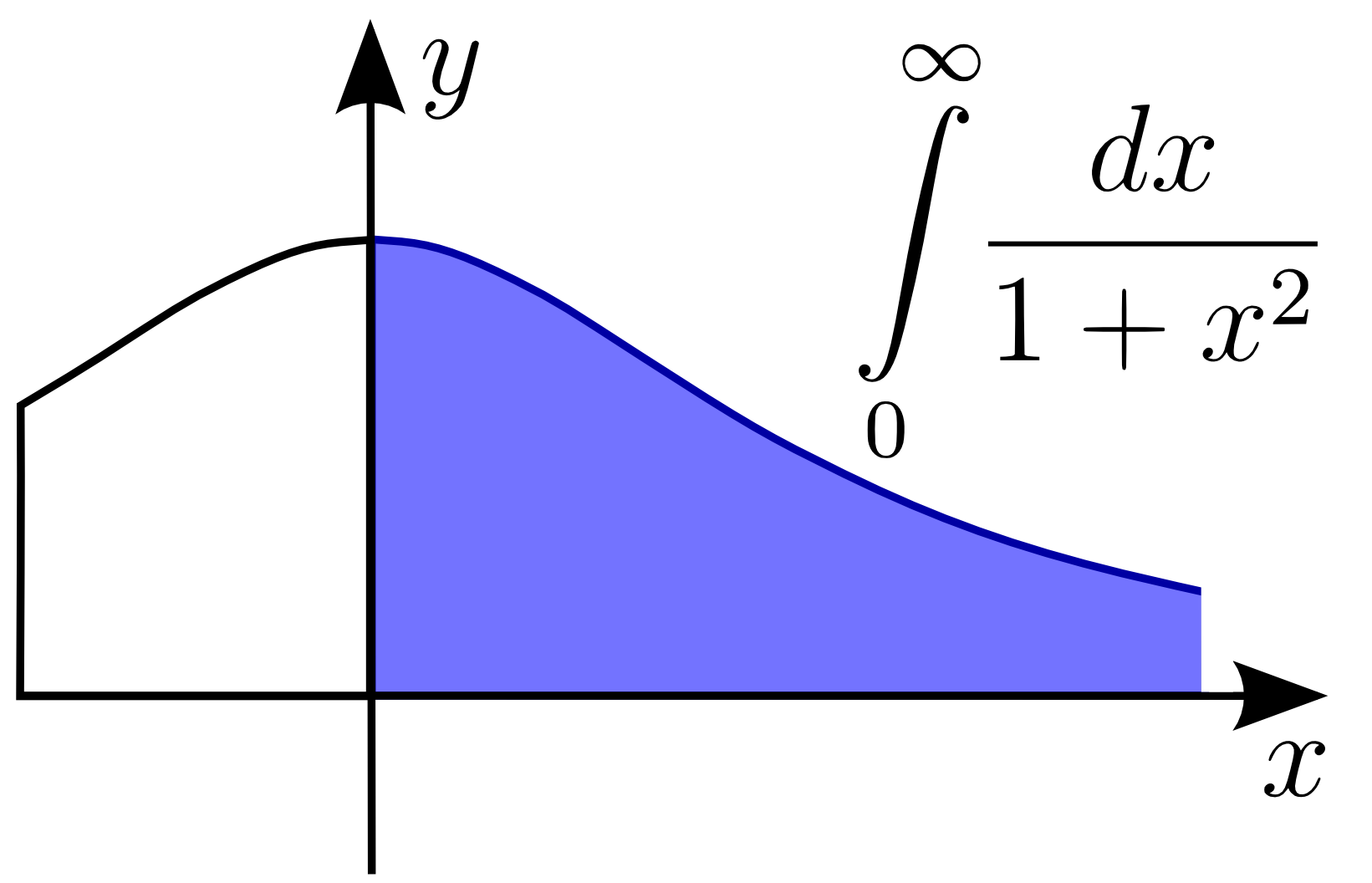
Improper Integral
In mathematical analysis, an improper integral is an extension of the notion of a definite integral to cases that violate the usual assumptions for that kind of integral. In the context of Riemann integrals (or, equivalently, Darboux integrals), this typically involves unboundedness, either of the set over which the integral is taken or of the integrand (the function being integrated), or both. It may also involve bounded but not closed sets or bounded but not continuous functions. While an improper integral is typically written symbolically just like a standard definite integral, it actually represents a limit of a definite integral or a sum of such limits; thus improper integrals are said to converge or diverge. If a regular definite integral (which may retronymically be called a proper integral) is worked out as if it is improper, the same answer will result. In the simplest case of a real-valued function of a single variable integrated in the sense of Riemann (or Darbou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Divergent Series
In mathematics, a divergent series is an infinite series that is not convergent, meaning that the infinite sequence of the partial sums of the series does not have a finite limit. If a series converges, the individual terms of the series must approach zero. Thus any series in which the individual terms do not approach zero diverges. However, convergence is a stronger condition: not all series whose terms approach zero converge. A counterexample is the harmonic series :1 + \frac + \frac + \frac + \frac + \cdots =\sum_^\infty\frac. The divergence of the harmonic series was proven by the medieval mathematician Nicole Oresme. In specialized mathematical contexts, values can be objectively assigned to certain series whose sequences of partial sums diverge, in order to make meaning of the divergence of the series. A ''summability method'' or ''summation method'' is a partial function from the set of series to values. For example, Cesàro summation assigns Grandi's divergent ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Yakov Zeldovich
Yakov Borisovich Zeldovich (, ; 8 March 1914 – 2 December 1987), also known as YaB, was a leading Soviet people, Soviet Physics, physicist of Belarusians, Belarusian origin, who is known for his prolific contributions in physical Physical cosmology, cosmology, physics of Plasma physics, thermonuclear reactions, combustion, and Fluid dynamics, hydrodynamical phenomena. From 1943, Zeldovich, a self-taught physicist, started his career by playing a crucial role in the development of the former Soviet atomic bomb project, Soviet program of nuclear weapons. In 1963, he returned to academia to embark on pioneering contributions on the fundamental understanding of the Black hole thermodynamics, thermodynamics of black holes and expanding the scope of physical cosmology. Biography Early life and education Yakov Zeldovich was born into a History of the Jews in Belarus, Belarusian Jewish family in his grandfather's house in Minsk. However, in mid-1914, the Zeldovich family moved to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gamow Factor
The Gamow factor, Sommerfeld factor or Gamow–Sommerfeld factor, named after physicists George Gamow or after Arnold Sommerfeld, is a probability factor for two nuclear particles' chance of overcoming the Coulomb barrier in order to undergo nuclear reactions, for example in nuclear fusion. By classical physics, there is almost no possibility for protons to fuse by crossing each other's Coulomb barrier at temperatures commonly observed to cause fusion, such as those found in the Sun. In 1927 it was discovered that there is a significant chance for nuclear fusion due to quantum tunnelling. While the probability of overcoming the Coulomb barrier increases rapidly with increasing particle energy, for a given temperature, the probability of a particle having such an energy falls off very fast, as described by the Maxwell–Boltzmann distribution. Gamow found that, taken together, these effects mean that for any given temperature, the particles that fuse are mostly in a temperature-dep ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
