|
Synge's World Function
In general relativity, Synge's world function is a smooth locally defined function of pairs of points in a smooth spacetime M with smooth Lorentzian metric g . Let x, x' be two points in spacetime, and suppose x belongs to a convex normal neighborhood U of x, x' (referred to the Levi-Civita connection associated to g ) so that there exists a unique geodesic \gamma(\lambda) from x to x' included in U, up to the affine parameter \lambda. Suppose \gamma(\lambda_0) = x' and \gamma(\lambda_1) = x. Then Synge's world function is defined as: :\sigma(x,x') = \frac (\lambda_-\lambda_) \int_ g_(z) t^t^ d\lambda where t^= \frac is the tangent vector to the affinely parametrized geodesic \gamma(\lambda). That is, \sigma(x,x') is half the square of the signed geodesic length from x to x' computed along the unique geodesic segment, in U, joining the two points. Synge's world function is well-defined, since the integral above is invariant under reparameterization. In particular, for Minkowski spac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
General Relativity
General relativity, also known as the general theory of relativity and Einstein's theory of gravity, is the geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of gravitation in modern physics. General relativity generalizes special relativity and refines Newton's law of universal gravitation, providing a unified description of gravity as a geometric property of space and time or four-dimensional spacetime. In particular, the ' is directly related to the energy and momentum of whatever matter and radiation are present. The relation is specified by the Einstein field equations, a system of second order partial differential equations. Newton's law of universal gravitation, which describes classical gravity, can be seen as a prediction of general relativity for the almost flat spacetime geometry around stationary mass distributions. Some predictions of general relativity, however, are beyond Newton's law of universal gr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
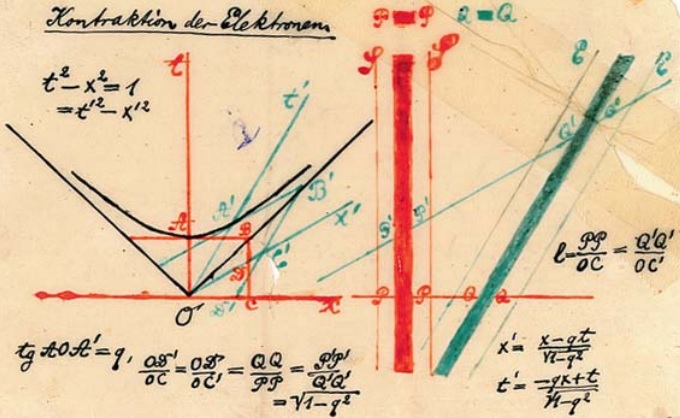
John Lighton Synge
John Lighton Synge (; 23 March 1897 – 30 March 1995) was an Irish mathematician and physicist, whose seven-decade career included significant periods in Ireland, Canada, and the USA. He was a prolific author and influential mentor, and is credited with the introduction of a new geometrical approach to the theory of relativity. Background Synge was born 1897 in Dublin, Ireland, into a prominent Church of Ireland family. He attended St. Andrew's College, Dublin and in 1915 entered Trinity College Dublin (TCD). He was elected a Foundation Scholar his first year, which was unusual as it was normally won by more advanced students. While an undergraduate at TCD, he spotted a non-trivial error in '' Analytical Dynamics'', a textbook by E. T. Whittaker, who had recently taught there, and notified Whittaker of the error. In 1919 he was awarded a B.A. in Mathematics and Experimental Physics, and also a gold medal for outstanding merit. In 1922 he was awarded an M.A., and in 1926 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spacetime
In physics, spacetime is a mathematical model that combines the three dimensions of space and one dimension of time into a single four-dimensional manifold. Spacetime diagrams can be used to visualize relativistic effects, such as why different observers perceive differently where and when events occur. Until the 20th century, it was assumed that the three-dimensional geometry of the universe (its spatial expression in terms of coordinates, distances, and directions) was independent of one-dimensional time. The physicist Albert Einstein helped develop the idea of spacetime as part of his theory of relativity. Prior to his pioneering work, scientists had two separate theories to explain physical phenomena: Isaac Newton's laws of physics described the motion of massive objects, while James Clerk Maxwell's electromagnetic models explained the properties of light. However, in 1905, Einstein based a work on special relativity on two postulates: * The laws of physics are invari ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lorentzian Metric
In differential geometry, a pseudo-Riemannian manifold, also called a semi-Riemannian manifold, is a differentiable manifold with a metric tensor that is everywhere nondegenerate. This is a generalization of a Riemannian manifold in which the requirement of positive-definiteness is relaxed. Every tangent space of a pseudo-Riemannian manifold is a pseudo-Euclidean vector space. A special case used in general relativity is a four-dimensional Lorentzian manifold for modeling spacetime, where tangent vectors can be classified as timelike, null, and spacelike. Introduction Manifolds In differential geometry, a differentiable manifold is a space which is locally similar to a Euclidean space. In an ''n''-dimensional Euclidean space any point can be specified by ''n'' real numbers. These are called the coordinates of the point. An ''n''-dimensional differentiable manifold is a generalisation of ''n''-dimensional Euclidean space. In a manifold it may only be possible to de ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Normal Neighborhood
In differential geometry, normal coordinates at a point ''p'' in a differentiable manifold equipped with a symmetric affine connection are a local coordinate system in a neighborhood of ''p'' obtained by applying the exponential map to the tangent space at ''p''. In a normal coordinate system, the Christoffel symbols of the connection vanish at the point ''p'', thus often simplifying local calculations. In normal coordinates associated to the Levi-Civita connection of a Riemannian manifold, one can additionally arrange that the metric tensor is the Kronecker delta at the point ''p'', and that the first partial derivatives of the metric at ''p'' vanish. A basic result of differential geometry states that normal coordinates at a point always exist on a manifold with a symmetric affine connection. In such coordinates the covariant derivative reduces to a partial derivative (at ''p'' only), and the geodesics through ''p'' are locally linear functions of ''t'' (the affine param ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Levi-Civita Connection
In Riemannian or pseudo Riemannian geometry (in particular the Lorentzian geometry of general relativity), the Levi-Civita connection is the unique affine connection on the tangent bundle of a manifold (i.e. affine connection) that preserves the ( pseudo-) Riemannian metric and is torsion-free. The fundamental theorem of Riemannian geometry states that there is a unique connection which satisfies these properties. In the theory of Riemannian and pseudo-Riemannian manifolds the term covariant derivative is often used for the Levi-Civita connection. The components (structure coefficients) of this connection with respect to a system of local coordinates are called Christoffel symbols. History The Levi-Civita connection is named after Tullio Levi-Civita, although originally "discovered" by Elwin Bruno Christoffel. Levi-Civita, along with Gregorio Ricci-Curbastro, used Christoffel's symbols to define the notion of parallel transport and explore the relationship of par ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geodesic
In geometry, a geodesic () is a curve representing in some sense the shortest path ( arc) between two points in a surface, or more generally in a Riemannian manifold. The term also has meaning in any differentiable manifold with a connection. It is a generalization of the notion of a "straight line". The noun '' geodesic'' and the adjective '' geodetic'' come from ''geodesy'', the science of measuring the size and shape of Earth, though many of the underlying principles can be applied to any ellipsoidal geometry. In the original sense, a geodesic was the shortest route between two points on the Earth's surface. For a spherical Earth, it is a segment of a great circle (see also great-circle distance). The term has since been generalized to more abstract mathematical spaces; for example, in graph theory, one might consider a geodesic between two vertices/nodes of a graph. In a Riemannian manifold or submanifold, geodesics are characterised by the property of having vanis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Minkowski Spacetime
In mathematical physics, Minkowski space (or Minkowski spacetime) () is a combination of three-dimensional Euclidean space and time into a four-dimensional manifold where the spacetime interval between any two events is independent of the inertial frame of reference in which they are recorded. Although initially developed by mathematician Hermann Minkowski for Maxwell's equations of electromagnetism, the mathematical structure of Minkowski spacetime was shown to be implied by the postulates of special relativity. Minkowski space is closely associated with Einstein's theories of special relativity and general relativity and is the most common mathematical structure on which special relativity is formulated. While the individual components in Euclidean space and time may differ due to length contraction and time dilation, in Minkowski spacetime, all frames of reference will agree on the total distance in spacetime between events.This makes spacetime distance an invar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spacetime Interval
In physics, spacetime is a mathematical model that combines the three dimensions of space and one dimension of time into a single four-dimensional manifold. Spacetime diagrams can be used to visualize relativistic effects, such as why different observers perceive differently where and when events occur. Until the 20th century, it was assumed that the three-dimensional geometry of the universe (its spatial expression in terms of coordinates, distances, and directions) was independent of one-dimensional time. The physicist Albert Einstein helped develop the idea of spacetime as part of his theory of relativity. Prior to his pioneering work, scientists had two separate theories to explain physical phenomena: Isaac Newton's laws of physics described the motion of massive objects, while James Clerk Maxwell's electromagnetic models explained the properties of light. However, in 1905, Einstein based a work on special relativity on two postulates: * The laws of physics are invaria ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multivalued Function
In mathematics, a multivalued function, also called multifunction, many-valued function, set-valued function, is similar to a function, but may associate several values to each input. More precisely, a multivalued function from a domain to a codomain associates each in to one or more values in ; it is thus a serial binary relation. Some authors allow a multivalued function to have no value for some inputs (in this case a multivalued function is simply a binary relation). However, in some contexts such as in complex analysis (''X'' = ''Y'' = C), authors prefer to mimic function theory as they extend concepts of the ordinary (single-valued) functions. In this context, an ordinary function is often called a single-valued function to avoid confusion. The term ''multivalued function'' originated in complex analysis, from analytic continuation. It often occurs that one knows the value of a complex analytic function f(z) in some neighbourhood of a point z=a. This is the cas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Field Theory In Curved Spacetime
In theoretical physics, quantum field theory in curved spacetime (QFTCS) is an extension of quantum field theory from Minkowski spacetime to a general curved spacetime. This theory treats spacetime as a fixed, classical background, while giving a quantum-mechanical description of the matter and energy propagating through that spacetime. A general prediction of this theory is that particles can be created by time-dependent gravitational fields (multi graviton pair production), or by time-independent gravitational fields that contain horizons. The most famous example of the latter is the phenomenon of Hawking radiation emitted by black holes. Overview Ordinary quantum field theories, which form the basis of standard model, are defined in flat Minkowski space, which is an excellent approximation when it comes to describing the behavior of microscopic particles in weak gravitational fields like those found on Earth. In order to describe situations in which gravity is strong eno ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parametrix
In mathematics, and specifically the field of partial differential equations (PDEs), a parametrix is an approximation to a fundamental solution of a PDE, and is essentially an approximate inverse to a differential operator. A parametrix for a differential operator is often easier to construct than a fundamental solution, and for many purposes is almost as good. It is sometimes possible to construct a fundamental solution from a parametrix by iteratively improving it. Overview and informal definition It is useful to review what a fundamental solution for a differential operator with constant coefficients is: it is a distribution on ℝ''n'' such that :P(D) = \delta(x)~, in the weak sense, where is the Dirac delta distribution. In a similar way, a parametrix for a variable coefficient differential operator is a distribution such that :P(x,D) = \delta(x) + \omega(x) ~, where is some function with compact support. The parametrix is a useful concept in the study of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |