Minkowski spacetime

In physics, Minkowski space (or Minkowski spacetime) () is the main mathematical description of spacetime in the absence of gravitation. It combines inertial space and time manifolds into a four-dimensional model.

The model helps show how a spacetime interval between any two events is independent of the inertial frame of reference in which they are recorded. Mathematician Hermann Minkowski developed it from the work of Hendrik Lorentz, Henri Poincaré, and others said it "was grown on experimental physical grounds".

Minkowski space is closely associated with Einstein's theories of special relativity and general relativity and is the most common mathematical structure by which special relativity is formalized. While the individual components in Euclidean space and time might differ due to length contraction and time dilation, in Minkowski spacetime, all frames of reference will agree on the total interval in spacetime between events.This makes spacetime distance an invariant. Minkowski space differs from four-dimensional Euclidean space insofar as it treats time differently from the three spatial dimensions.

In 3-dimensional Euclidean space, the isometry group (maps preserving the regular Euclidean distance) is the Euclidean group. It is generated by rotations, reflections and translations. When time is appended as a fourth dimension, the further transformations of translations in time and Lorentz boosts are added, and the group of all these transformations is called the Poincaré group. Minkowski's model follows special relativity, where motion causes time dilation changing the scale applied to the frame in motion and shifts the phase of light.

Minkowski space is a pseudo-Euclidean space equipped with an isotropic quadratic form called the spacetime interval or the ''Minkowski norm squared''. An event in Minkowski space for which the spacetime interval is zero is on the null cone of the origin, called the light cone in Minkowski space. Using the polarization identity the quadratic form is converted to a symmetric bilinear form called the ''Minkowski inner product'', though it is not a geometric inner product. Another misnomer is ''Minkowski metric'', but Minkowski space is not a metric space.

The group of transformations for Minkowski space that preserves the spacetime interval (as opposed to the spatial Euclidean distance) is the Lorentz group (as opposed to the Galilean group).

History

Complex Minkowski spacetime

In his second relativity paper in 1905, Henri Poincaré showed how, by taking time to be an imaginary fourth spacetime coordinate , where is the speed of light and is the imaginary unit, Lorentz transformations can be visualized as ordinary rotations of the four-dimensional Euclidean sphere. The four-dimensional spacetime can be visualized as a four-dimensional space, with each point representing an event in spacetime. The Lorentz transformations can then be thought of as rotations in this four-dimensional space, where the rotation axis corresponds to the direction of relative motion between the two observers and the rotation angle is related to their relative velocity.

To understand this concept, one should consider the coordinates of an event in spacetime represented as a four-vector . A Lorentz transformation is represented by a matrix that acts on the four-vector, changing its components. This matrix can be thought of as a rotation matrix in four-dimensional space, which rotates the four-vector around a particular axis.$x^2 + y^2 + z^2 + (ict)^2 = \text.$

Rotations in planes spanned by two space unit vectors appear in coordinate space as well as in physical spacetime as Euclidean rotations and are interpreted in the ordinary sense. The "rotation" in a plane spanned by a space unit vector and a time unit vector, while formally still a rotation in coordinate space, is a Lorentz boost in physical spacetime with ''real'' inertial coordinates. The analogy with Euclidean rotations is only partial since the radius of the sphere is actually imaginary, which turns rotations into rotations in hyperbolic space (see hyperbolic rotation).

This idea, which was mentioned only briefly by Poincaré, was elaborated by Minkowski in a paper in German published in 1908 called "The Fundamental Equations for Electromagnetic Processes in Moving Bodies". He reformulated Maxwell equations as a symmetrical set of equations in the four variables combined with redefined vector variables for electromagnetic quantities, and he was able to show directly and very simply their invariance under Lorentz transformation. He also made other important contributions and used matrix notation for the first time in this context.
From his reformulation, he concluded that time and space should be treated equally, and so arose his concept of events taking place in a unified four-dimensional spacetime continuum.

Real Minkowski spacetime

In a further development in his 1908 "Space and Time" lecture, Various English translations on Wikisource: "Space and Time" Minkowski gave an alternative formulation of this idea that used a real time coordinate instead of an imaginary one, representing the four variables of space and time in the coordinate form in a four-dimensional real vector space. Points in this space correspond to events in spacetime. In this space, there is a defined light-cone associated with each point, and events not on the light cone are classified by their relation to the apex as ''spacelike'' or ''timelike''. It is principally this view of spacetime that is current nowadays, although the older view involving imaginary time has also influenced special relativity.

In the English translation of Minkowski's paper, the Minkowski metric, as defined below, is referred to as the ''line element''. The Minkowski inner product below appears unnamed when referring to orthogonality (which he calls ''normality'') of certain vectors, and the Minkowski norm squared is referred to (somewhat cryptically, perhaps this is a translation dependent) as "sum".

Minkowski's principal tool is the Minkowski diagram, and he uses it to define concepts and demonstrate properties of Lorentz transformations (e.g., proper time and length contraction) and to provide geometrical interpretation to the generalization of Newtonian mechanics to relativistic mechanics. For these special topics, see the referenced articles, as the presentation below will be principally confined to the mathematical structure (Minkowski metric and from it derived quantities and the Poincaré group as symmetry group of spacetime) ''following'' from the invariance of the spacetime interval on the spacetime manifold as consequences of the postulates of special relativity, not to specific application or ''derivation'' of the invariance of the spacetime interval. This structure provides the background setting of all present relativistic theories, barring general relativity for which flat Minkowski spacetime still provides a springboard as curved spacetime is locally Lorentzian.

Minkowski, aware of the fundamental restatement of the theory which he had made, said

Though Minkowski took an important step for physics, Albert Einstein saw its limitation:

For further historical information see references , and .

Causal structure

Where is velocity, , , and are Cartesian coordinates in 3-dimensional space, is the constant representing the universal speed limit, and is time, the four-dimensional vector is classified according to the sign of . A vector is timelike if , spacelike if , and null or lightlike if . This can be expressed in terms of the sign of , also called scalar product, as well, which depends on the signature. The classification of any vector will be the same in all frames of reference that are related by a Lorentz transformation (but not by a general Poincaré transformation because the origin may then be displaced) because of the invariance of the spacetime interval under Lorentz transformation.

The set of all null vectors at an eventTranslate the coordinate system so that the event is the new origin. of Minkowski space constitutes the light cone of that event. Given a timelike vector , there is a worldline of constant velocity associated with it, represented by a straight line in a Minkowski diagram.

Once a direction of time is chosen,This corresponds to the time coordinate either increasing or decreasing when the proper time for any particle increases. An application of flips this direction. timelike and null vectors can be further decomposed into various classes. For timelike vectors, one has
# future-directed timelike vectors whose first component is positive (tip of vector located in causal future (also called the absolute future) in the figure) and
# past-directed timelike vectors whose first component is negative (causal past (also called the absolute past)).
Null vectors fall into three classes:
# the zero vector, whose components in any basis are (origin),
# future-directed null vectors whose first component is positive (upper light cone), and
# past-directed null vectors whose first component is negative (lower light cone).
Together with spacelike vectors, there are 6 classes in all.

An orthonormal basis for Minkowski space necessarily consists of one timelike and three spacelike unit vectors. If one wishes to work with non-orthonormal bases, it is possible to have other combinations of vectors. For example, one can easily construct a (non-orthonormal) basis consisting entirely of null vectors, called a null basis.

Vector fields are called timelike, spacelike, or null if the associated vectors are timelike, spacelike, or null at each point where the field is defined.

Properties of time-like vectors

Time-like vectors have special importance in the theory of relativity as they correspond to events that are accessible to the observer at (0, 0, 0, 0) with a speed less than that of light. Of most interest are time-like vectors that are ''similarly directed'', i.e. all either in the forward or in the backward cones. Such vectors have several properties not shared by space-like vectors. These arise because both forward and backward cones are convex, whereas the space-like region is not convex.

Scalar product

The scalar product of two time-like vectors and is
$\eta (u_1, u_2) = u_1 \cdot u_2 = c^2 t_1 t_2 - x_1 x_2 - y_1 y_2 - z_1 z_2 .$

''Positivity of scalar product'': An important property is that the scalar product of two similarly directed time-like vectors is always positive. This can be seen from the reversed Cauchy–Schwarz inequality below. It follows that if the scalar product of two vectors is zero, then one of these, at least, must be space-like. The scalar product of two space-like vectors can be positive or negative as can be seen by considering the product of two space-like vectors having orthogonal spatial components and times either of different or the same signs.

Using the positivity property of time-like vectors, it is easy to verify that a linear sum with positive coefficients of similarly directed time-like vectors is also similarly directed time-like (the sum remains within the light cone because of convexity).

Norm and reversed Cauchy inequality

The norm of a time-like vector is defined as
$\left\, u \right\, = \sqrt = \sqrt$

''The reversed Cauchy inequality'' is another consequence of the convexity of either light cone. For two distinct similarly directed time-like vectors and this inequality is
$\eta(u_1, u_2) > \left\, u_1 \right\, \left\, u_2 \right\,$
or algebraically,
$c^2 t_1 t_2 - x_1 x_2 - y_1 y_2 - z_1 z_2 > \sqrt$

From this, the positive property of the scalar product can be seen.

Reversed triangle inequality

For two similarly directed time-like vectors and , the inequality is
$\left\, u + w \right\, \ge \left\, u \right\, + \left\, w \right\, ,$
where the equality holds when the vectors are linearly dependent.

The proof uses the algebraic definition with the reversed Cauchy inequality:
\begin
\left\, u + w \right\, ^2
&= \left\, u \right\, ^2 + 2 \left(u, w \right) + \left\, w \right\, ^2 \\ mu&\ge \left\, u \right\, ^2 +2 \left\, u \right\, \left\, w \right\, + \left\, w \right\, ^2
= \left( \left\, u \right\, + \left\, w \right\, \right)^2.
\end

The result now follows by taking the square root on both sides.

Mathematical structure

It is assumed below that spacetime is endowed with a coordinate system corresponding to an inertial frame. This provides an ''origin'', which is necessary for spacetime to be modeled as a vector space. This addition is not required, and more complex treatments analogous to an affine space can remove the extra structure. However, this is not the introductory convention and is not covered here.

For an overview, Minkowski space is a -dimensional real vector space equipped with a non-degenerate, symmetric bilinear form on the tangent space at each point in spacetime, here simply called the ''Minkowski inner product'', with metric signature either or . The tangent space at each event is a vector space of the same dimension as spacetime, .

Tangent vectors

In practice, one need not be concerned with the tangent spaces. The vector space structure of Minkowski space allows for the canonical identification of vectors in tangent spaces at points (events) with vectors (points, events) in Minkowski space itself. See e.g. or These identifications are routinely done in mathematics. They can be expressed formally in Cartesian coordinates as
$\begin \left(x^0,\, x^1,\, x^2,\, x^3\right) \ &\leftrightarrow\ \left. x^0 \mathbf e_0 \_p + \left. x^1 \mathbf e_1 \_p + \left. x^2 \mathbf e_2 \_p + \left. x^3 \mathbf e_3 \_p \\ &\leftrightarrow\ \left. x^0 \mathbf e_0 \_q + \left. x^1 \mathbf e_1 \_q + \left. x^2 \mathbf e_2 \_q + \left. x^3 \mathbf e_3 \_q \end$
with basis vectors in the tangent spaces defined by
$\left.\mathbf e_\mu\_p = \left.\frac\_p \text \mathbf e_0, _p = \left(\begin 1 \\ 0 \\ 0 \\ 0\end\right) \text.$

Here, and are any two events, and the second basis vector identification is referred to as parallel transport. The first identification is the canonical identification of vectors in the tangent space at any point with vectors in the space itself. The appearance of basis vectors in tangent spaces as first-order differential operators is due to this identification. It is motivated by the observation that a geometrical tangent vector can be associated in a one-to-one manner with a directional derivative operator on the set of smooth functions. This is promoted to a ''definition'' of tangent vectors in manifolds ''not'' necessarily being embedded in . This definition of tangent vectors is not the only possible one, as ordinary ''n''-tuples can be used as well.

A tangent vector at a point may be defined, here specialized to Cartesian coordinates in Lorentz frames, as column vectors associated to ''each'' Lorentz frame related by Lorentz transformation such that the vector in a frame related to some frame by transforms according to . This is the ''same'' way in which the coordinates transform. Explicitly,
$\begin x'^\mu &= _\nu x^\nu, \\ v'^\mu &= _\nu v^\nu. \end$

This definition is equivalent to the definition given above under a canonical isomorphism.

For some purposes, it is desirable to identify tangent vectors at a point with ''displacement vectors'' at , which is, of course, admissible by essentially the same canonical identification. The identifications of vectors referred to above in the mathematical setting can correspondingly be found in a more physical and explicitly geometrical setting in . They offer various degrees of sophistication (and rigor) depending on which part of the material one chooses to read.

Metric signature

The metric signature refers to which sign the Minkowski inner product yields when given space (''spacelike'' to be specific, defined further down) and time basis vectors (''timelike'') as arguments. Further discussion about this theoretically inconsequential but practically necessary choice for purposes of internal consistency and convenience is deferred to the hide box below. See also the page treating sign convention in Relativity.

In general, but with several exceptions, mathematicians and general relativists prefer spacelike vectors to yield a positive sign, , while particle physicists tend to prefer timelike vectors to yield a positive sign, . Authors covering several areas of physics, e.g. Steven Weinberg and Landau and Lifshitz and , respectively stick to one choice regardless of topic. Arguments for the former convention include "continuity" from the Euclidean case corresponding to the non-relativistic limit . Arguments for the latter include that minus signs, otherwise ubiquitous in particle physics, go away. Yet other authors, especially of introductory texts, e.g. , do ''not'' choose a signature at all, but instead, opt to coordinatize spacetime such that the time ''coordinate'' (but not time itself!) is imaginary. This removes the need for the ''explicit'' introduction of a metric tensor (which may seem like an extra burden in an introductory course), and one needs ''not'' be concerned with covariant vectors and contravariant vectors (or raising and lowering indices) to be described below. The inner product is instead affected by a straightforward extension of the dot product from over to This works in the flat spacetime of special relativity, but not in the curved spacetime of general relativity, see who, by the way use MTW also argues that it hides the true ''indefinite'' nature of the metric and the true nature of Lorentz boosts, which are not rotations. It also needlessly complicates the use of tools of differential geometry that are otherwise immediately available and useful for geometrical description and calculation – even in the flat spacetime of special relativity, e.g. of the electromagnetic field.

Terminology

Mathematically associated with the bilinear form is a tensor of type at each point in spacetime, called the ''Minkowski metric''.For comparison and motivation of terminology, take a Riemannian metric, which provides a positive definite symmetric bilinear form, i. e. an inner product proper at each point on a manifold. The Minkowski metric, the bilinear form, and the Minkowski inner product are all the same object; it is a bilinear function that accepts two (contravariant) vectors and returns a real number. In coordinates, this is the matrix representing the bilinear form.

For comparison, in general relativity, a Lorentzian manifold is likewise equipped with a metric tensor , which is a nondegenerate symmetric bilinear form on the tangent space at each point of . In coordinates, it may be represented by a matrix ''depending on spacetime position''. Minkowski space is thus a comparatively simple special case of a Lorentzian manifold. Its metric tensor is in coordinates with the same symmetric matrix at every point of , and its arguments can, per above, be taken as vectors in spacetime itself.

Introducing more terminology (but not more structure), Minkowski space is thus a pseudo-Euclidean space with total dimension and signature or . Elements of Minkowski space are called events. Minkowski space is often denoted or to emphasize the chosen signature, or just . It is an example of a pseudo-Riemannian manifold.

Then mathematically, the metric is a bilinear form on an abstract four-dimensional real vector space , that is,
$\eta:V\times V\rightarrow \mathbf$
where has signature , and signature is a coordinate-invariant property of . The space of bilinear maps forms a vector space which can be identified with $M^*\otimes M^*$, and may be equivalently viewed as an element of this space. By making a choice of orthonormal basis $\$, $M:=(V,\eta)$ can be identified with the space $\mathbf^:=(\mathbf^,\eta_)$. The notation is meant to emphasize the fact that and $\mathbf^$ are not just vector spaces but have added structure. $\eta_ = \text(+1, -1, -1, -1)$.

An interesting example of non-inertial coordinates for (part of) Minkowski spacetime is the Born coordinates. Another useful set of coordinates is the light-cone coordinates.

Pseudo-Euclidean metrics

The Minkowski inner product is not an inner product, since it has non-zero null vectors. Since it is not a definite bilinear form it is called ''indefinite''.

The Minkowski metric is the metric tensor of Minkowski space. It is a pseudo-Euclidean metric, or more generally, a ''constant'' pseudo-Riemannian metric in Cartesian coordinates. As such, it is a nondegenerate symmetric bilinear form, a type tensor. It accepts two arguments , vectors in , the tangent space at in . Due to the above-mentioned canonical identification of with itself, it accepts arguments with both and in .

As a notational convention, vectors in , called 4-vectors, are denoted in italics, and not, as is common in the Euclidean setting, with boldface . The latter is generally reserved for the -vector part (to be introduced below) of a -vector.

The definition
$u \cdot v = \eta(u,\, v)$
yields an inner product-like structure on , previously and also henceforth, called the ''Minkowski inner product'', similar to the Euclidean inner product, but it describes a different geometry. It is also called the ''relativistic dot product''. If the two arguments are the same,
$u \cdot u = \eta(u, u) \equiv \, u\, ^2 \equiv u^2,$
the resulting quantity will be called the ''Minkowski norm squared''. The Minkowski inner product satisfies the following properties.

; Linearity in the first argument
: $\eta(au + v,\, w) = a\eta(u,\, w) + \eta(v,\, w),\quad \forall u,\, v \in M,\; \forall a \in \R$
; Symmetry
: $\eta(u,\, v) = \eta(v,\, u)$
; Non-degeneracy
: $\eta(u,\, v) = 0,\; \forall v \in M\ \Rightarrow\ u = 0$

The first two conditions imply bilinearity.

The most important feature of the inner product and norm squared is that ''these are quantities unaffected by Lorentz transformations''. In fact, it can be taken as the defining property of a Lorentz transformation in that it preserves the inner product (i.e. the value of the corresponding bilinear form on two vectors). This approach is taken more generally for ''all'' classical groups definable this way in classical group. There, the matrix is identical in the case (the Lorentz group) to the matrix to be displayed below.

Orthogonality

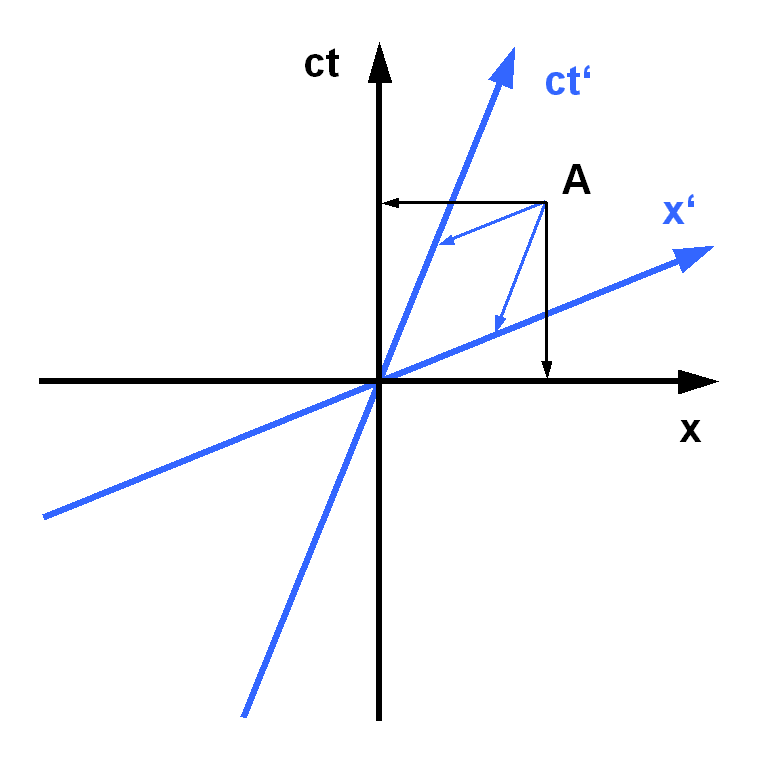
Minkowski space is constructed so that the speed of light will be the same constant regardless of the reference frame in which it is measured. This property results from the relation of the time axis to a space axis. Two events ''u'' and ''v'' are orthogonal when the bilinear form is zero for them: .

When both ''u'' and ''v'' are both space-like, then they are perpendicular, but if one is time-like and the other space-like, then the relation is hyperbolic orthogonality. The relation is preserved in a change of reference frames and consequently the computation of light speed yields a constant result. The change of reference frame is called a Lorentz boost and in mathematics it is a hyperbolic rotation. Each reference frame is associated with a hyperbolic angle, which is zero for the rest frame in Minkowski space. Such a hyperbolic angle has been labelled rapidity since it is associated with the speed of the frame.

Minkowski metric

From the second postulate of special relativity, together with homogeneity of spacetime and isotropy of space, it follows that the spacetime interval between two arbitrary events called and is:
$c^2\left(t_1 - t_2\right)^2 - \left(x_1 - x_2\right)^2 - \left(y_1 - y_2\right)^2 - \left(z_1 - z_2\right)^2.$
This quantity is not consistently named in the literature. The interval is sometimes referred to as the square root of the interval as defined here.

The invariance of the interval under coordinate transformations between inertial frames follows from the invariance of
$c^2 t^2 - x^2 - y^2 - z^2$
provided the transformations are linear. This quadratic form can be used to define a bilinear form
$u \cdot v = c^2 t_1 t_2 - x_1 x_2 - y_1 y_2 - z_1 z_2$
via the polarization identity. This bilinear form can in turn be written as
$u \cdot v = u^\textsf \,$eta\, v,
where is a $4\times 4$ matrix associated with . While possibly confusing, it is common practice to denote with just . The matrix is read off from the explicit bilinear form as
$\eta = \left(\begin 1 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & -1 \end\right)\!,$
and the bilinear form
$u \cdot v = \eta(u, v),$
with which this section started by assuming its existence, is now identified.

For definiteness and shorter presentation, the signature is adopted below. This choice (or the other possible choice) has no (known) physical implications. The symmetry group preserving the bilinear form with one choice of signature is isomorphic (under the map given here) with the symmetry group preserving the other choice of signature. This means that both choices are in accord with the two postulates of relativity. Switching between the two conventions is straightforward. If the metric tensor has been used in a derivation, go back to the earliest point where it was used, substitute for , and retrace forward to the desired formula with the desired metric signature.

Standard basis

A standard or orthonormal basis for Minkowski space is a set of four mutually orthogonal vectors such that
$\eta(e_0, e_0) = -\eta(e_1, e_1) = -\eta(e_2, e_2) = -\eta(e_3, e_3) = 1$
and for which $\eta(e_\mu, e_\nu) = 0$ when $\mu \neq \nu\,.$

These conditions can be written compactly in the form
$\eta(e_\mu, e_\nu) = \eta_.$

Relative to a standard basis, the components of a vector are written where the Einstein notation is used to write . The component is called the timelike component of while the other three components are called the spatial components. The spatial components of a -vector may be identified with a -vector .

In terms of components, the Minkowski inner product between two vectors and is given by

$\eta(v, w) = \eta_ v^\mu w^\nu = v^0 w_0 + v^1 w_1 + v^2 w_2 + v^3 w_3 = v^\mu w_\mu = v_\mu w^\mu,$
and
$\eta(v, v) = \eta_ v^\mu v^\nu = v^0v_0 + v^1 v_1 + v^2 v_2 + v^3 v_3 = v^\mu v_\mu.$

Here lowering of an index with the metric was used.

There are many possible choices of standard basis obeying the condition $\eta(e_\mu, e_\nu) = \eta_.$ Any two such bases are related in some sense by a Lorentz transformation, either by a change-of-basis matrix $\Lambda^\mu_\nu$, a real matrix satisfying
$\Lambda^\mu_\rho\eta_\Lambda^\nu_\sigma = \eta_.$
or , a linear map on the abstract vector space satisfying, for any pair of vectors , ,
$\eta(\Lambda u, \Lambda v) = \eta(u, v).$

Then if two different bases exist, and , $e_\mu' = e_\nu\Lambda^\nu_\mu$ can be represented as $e_\mu' = e_\nu\Lambda^\nu_\mu$ or $e_\mu' = \Lambda e_\mu$. While it might be tempting to think of $\Lambda^\mu_\nu$ and as the same thing, mathematically, they are elements of different spaces, and act on the space of standard bases from different sides.

Raising and lowering of indices

Technically, a non-degenerate bilinear form provides a map between a vector space and its dual; in this context, the map is between the tangent spaces of and the cotangent spaces of . At a point in , the tangent and cotangent spaces are dual vector spaces (so the dimension of the cotangent space at an event is also ). Just as an authentic inner product on a vector space with one argument fixed, by Riesz representation theorem, may be expressed as the action of a linear functional on the vector space, the same holds for the Minkowski inner product of Minkowski space.

Thus if are the components of a vector in tangent space, then are the components of a vector in the cotangent space (a linear functional). Due to the identification of vectors in tangent spaces with vectors in itself, this is mostly ignored, and vectors with lower indices are referred to as covariant vectors. In this latter interpretation, the covariant vectors are (almost always implicitly) identified with vectors (linear functionals) in the dual of Minkowski space. The ones with upper indices are contravariant vectors. In the same fashion, the inverse of the map from tangent to cotangent spaces, explicitly given by the inverse of in matrix representation, can be used to define raising of an index. The components of this inverse are denoted . It happens that . These maps between a vector space and its dual can be denoted (eta-flat) and (eta-sharp) by the musical analogy.

Contravariant and covariant vectors are geometrically very different objects. The first can and should be thought of as arrows. A linear function can be characterized by two objects: its kernel, which is a hyperplane passing through the origin, and its norm. Geometrically thus, covariant vectors should be viewed as a set of hyperplanes, with spacing depending on the norm (bigger = smaller spacing), with one of them (the kernel) passing through the origin. The mathematical term for a covariant vector is 1-covector or 1-form (though the latter is usually reserved for covector ''fields'').

One quantum mechanical analogy explored in the literature is that of a de Broglie wave (scaled by a factor of Planck's reduced constant) associated with a momentum four-vector to illustrate how one could imagine a covariant version of a contravariant vector. The inner product of two contravariant vectors could equally well be thought of as the action of the covariant version of one of them on the contravariant version of the other. The inner product is then how many times the arrow pierces the planes. The mathematical reference, , offers the same geometrical view of these objects (but mentions no piercing).

The electromagnetic field tensor is a differential 2-form, which geometrical description can as well be found in MTW.

One may, of course, ignore geometrical views altogether (as is the style in e.g. and ) and proceed algebraically in a purely formal fashion. The time-proven robustness of the formalism itself, sometimes referred to as index gymnastics, ensures that moving vectors around and changing from contravariant to covariant vectors and vice versa (as well as higher order tensors) is mathematically sound. Incorrect expressions tend to reveal themselves quickly.

Coordinate free raising and lowering

Given a bilinear form $\ \eta : M \times M \rightarrow \mathbb\ ,$ the lowered version of a vector can be thought of as the partial evaluation of $\ \eta\ ,$ that is, there is an associated partial evaluation map
$\eta(\cdot, -) : M \rightarrow M^*\ ~,\quad v \mapsto \eta(v,\cdot) ~.$

The lowered vector $\ \eta(v,\cdot) \in M^*\$ is then the dual map $\ u \mapsto \eta(v,u) ~.$ Note it does not matter which argument is partially evaluated due to the symmetry of $\ \eta ~.$

Non-degeneracy is then equivalent to injectivity of the partial evaluation map, or equivalently non-degeneracy indicates that the kernel of the map is trivial. In finite dimension, as is the case here, and noting that the dimension of a finite-dimensional space is equal to the dimension of the dual, this is enough to conclude the partial evaluation map is a linear isomorphism from $\ M\$ to $\ M^* ~.$ This then allows the definition of the inverse partial evaluation map,
$\eta^ : M^* \rightarrow M\ ,$
which allows the inverse metric to be defined as
$\eta^ : M^* \times M^* \rightarrow \mathbb\ ~,\quad \eta^\!(\alpha,\beta)\ =\ \eta\bigl(\ \eta^\!(\alpha),\ \eta^\!(\beta)\ \bigr)\$
where the two different usages of $\; \eta^\$ can be told apart by the argument each is evaluated on. This can then be used to raise indices. If a coordinate basis is used, the metric is indeed the matrix inverse to

Formalism of the Minkowski metric

The present purpose is to show semi-rigorously how ''formally'' one may apply the Minkowski metric to two vectors and obtain a real number, i.e. to display the role of the differentials and how they disappear in a calculation. The setting is that of smooth manifold theory, and concepts such as convector fields and exterior derivatives are introduced.

A full-blown version of the Minkowski metric in coordinates as a tensor field on spacetime has the appearance
$\eta_ \operatornamex^\mu \otimes \operatornamex^\nu = \eta_ \operatornamex^\mu \odot \operatornamex^\nu = \eta_ \operatornamex^\mu \operatornamex^\nu ~.$

Explanation: The coordinate differentials are 1-form fields. They are defined as the exterior derivative of the coordinate functions . These quantities evaluated at a point provide a basis for the cotangent space at . The tensor product (denoted by the symbol ) yields a tensor field of type , i.e. the type that expects two contravariant vectors as arguments. On the right-hand side, the symmetric product (denoted by the symbol or by juxtaposition) has been taken. The equality holds since, by definition, the Minkowski metric is symmetric. The notation on the far right is also sometimes used for the related, but different, line element. It is ''not'' a tensor. For elaboration on the differences and similarities, see

''Tangent'' vectors are, in this formalism, given in terms of a basis of differential operators of the first order,
$\left.\frac\_p\ ,$
where is an event. This operator applied to a function gives the directional derivative of at in the direction of increasing with fixed. They provide a basis for the tangent space at .

The exterior derivative of a function is a covector field, i.e. an assignment of a cotangent vector to each point , by definition such that
$\operatornamef(X) = X\ f,$
for each vector field . A vector field is an assignment of a tangent vector to each point . In coordinates can be expanded at each point in the basis given by the Applying this with , the coordinate function itself, and called a ''coordinate vector field'', one obtains
$\operatornamex^\mu\left(\frac\right) = \frac = \delta_\nu^\mu ~.$

Since this relation holds at each point , the provide a basis for the cotangent space at each and the bases and are dual to each other,
$\Bigl.\operatornamex^\mu \Bigr, _p \left(\left.\frac\_p\right) = \delta^\mu_\nu ~.$
at each . Furthermore, one has
$\alpha\ \otimes\ \beta(a, b)\ =\ \alpha(a)\ \beta(b)\$
for general one-forms on a tangent space and general tangent vectors . (This can be taken as a definition, but may also be proved in a more general setting.)

Thus when the metric tensor is fed two vectors fields , , both expanded in terms of the basis coordinate vector fields, the result is
$\eta_\ \operatornamex^\mu \otimes \operatornamex^\nu(a, b)\ =\ \eta_\ a^\mu\ b^\nu\ ,$
where , are the ''component functions'' of the vector fields. The above equation holds at each point , and the relation may as well be interpreted as the Minkowski metric at applied to two tangent vectors at .

As mentioned, in a vector space, such as modeling the spacetime of special relativity, tangent vectors can be canonically identified with vectors in the space itself, and vice versa. This means that the tangent spaces at each point are canonically identified with each other and with the vector space itself. This explains how the right-hand side of the above equation can be employed directly, without regard to the spacetime point the metric is to be evaluated and from where (which tangent space) the vectors come from.

This situation changes in general relativity. There one has
$g_\!(p)\ \Bigl.\operatornamex^\mu \Bigr, _p\ \left. \operatornamex^\nu \_p(a, b)\ =\ g_\!(p)\ a^\mu\ b^\nu\ ,$
where now , i.e., is still a metric tensor but now depending on spacetime and is a solution of Einstein's field equations. Moreover, ''must'' be tangent vectors at spacetime point and can no longer be moved around freely.

Chronological and causality relations

Let . Here,
# chronologically precedes if is future-directed timelike. This relation has the transitive property and so can be written .
# causally precedes if is future-directed null or future-directed timelike. It gives a partial ordering of spacetime and so can be written .

Suppose is timelike. Then the simultaneous hyperplane for is . Since this hyperplane varies as varies, there is a relativity of simultaneity in Minkowski space.

Generalizations

A Lorentzian manifold is a generalization of Minkowski space in two ways. The total number of spacetime dimensions is not restricted to be ( or more) and a Lorentzian manifold need not be flat, i.e. it allows for curvature.

Complexified Minkowski space

Complexified Minkowski space is defined as . Its real part is the Minkowski space of four-vectors, such as the four-velocity and the four-momentum, which are independent of the choice of orientation of the space. The imaginary part, on the other hand, may consist of four pseudovectors, such as angular velocity and magnetic moment, which change their direction with a change of orientation. A pseudoscalar is introduced, which also changes sign with a change of orientation. Thus, elements of are independent of the choice of the orientation.

The inner product-like structure on is defined as for any . A relativistic pure spin of an electron or any half spin particle is described by as , where is the four-velocity of the particle, satisfying and is the 4D spin vector, which is also the Pauli–Lubanski pseudovector satisfying and .

Generalized Minkowski space

Minkowski space refers to a mathematical formulation in four dimensions. However, the mathematics can easily be extended or simplified to create an analogous generalized Minkowski space in any number of dimensions. If , -dimensional Minkowski space is a vector space of real dimension on which there is a constant Minkowski metric of signature or . These generalizations are used in theories where spacetime is assumed to have more or less than dimensions. String theory and M-theory are two examples where . In string theory, there appears conformal field theories with spacetime dimensions.

de Sitter space can be formulated as a submanifold of generalized Minkowski space as can the model spaces of hyperbolic geometry (see below).

Curvature

As a flat spacetime, the three spatial components of Minkowski spacetime always obey the Pythagorean Theorem. Minkowski space is a suitable basis for special relativity, a good description of physical systems over finite distances in systems without significant gravitation. However, in order to take gravity into account, physicists use the theory of general relativity, which is formulated in the mathematics of differential geometry of differential manifolds. When this geometry is used as a model of spacetime, it is known as curved spacetime.

Even in curved spacetime, Minkowski space is still a good description in an infinitesimal region surrounding any point (barring gravitational singularities).This similarity between flat space and curved space at infinitesimally small distance scales is foundational to the definition of a manifold in general. More abstractly, it can be said that in the presence of gravity spacetime is described by a curved 4-dimensional manifold for which the tangent space to any point is a 4-dimensional Minkowski space. Thus, the structure of Minkowski space is still essential in the description of general relativity.

Geometry

The meaning of the term ''geometry'' for the Minkowski space depends heavily on the context. Minkowski space is not endowed with Euclidean geometry, and not with any of the generalized Riemannian geometries with intrinsic curvature, those exposed by the ''model spaces'' in hyperbolic geometry (negative curvature) and the geometry modeled by the sphere (positive curvature). The reason is the indefiniteness of the Minkowski metric. Minkowski space is, in particular, not a metric space and not a Riemannian manifold with a Riemannian metric. However, Minkowski space contains submanifolds endowed with a Riemannian metric yielding hyperbolic geometry.

Model spaces of hyperbolic geometry of low dimension, say 2 or 3, ''cannot'' be isometrically embedded in Euclidean space with one more dimension, i.e. $\mathbf^3$ or $\mathbf^4$ respectively, with the Euclidean metric $\overline$, preventing easy visualization.There ''is'' an isometric embedding into according to the Nash embedding theorem (), but the embedding dimension is much higher, for a Riemannian manifold of dimension . By comparison, model spaces with positive curvature are just spheres in Euclidean space of one higher dimension. Hyperbolic spaces ''can'' be isometrically embedded in spaces of one more dimension when the embedding space is endowed with the Minkowski metric $\eta$.

Define $\mathbf^_R \subset \mathbf^$to be the upper sheet ($ct > 0$) of the hyperboloid
$\mathbf H_R^ = \left\$
in generalized Minkowski space $\mathbf^$ of spacetime dimension $n + 1.$ This is one of the surfaces of transitivity of the generalized Lorentz group. The induced metric on this submanifold,
$h_R^ = \iota^* \eta,$
the pullback of the Minkowski metric $\eta$ under inclusion, is a Riemannian metric. With this metric $\mathbf^_R$ is a Riemannian manifold. It is one of the model spaces of Riemannian geometry, the hyperboloid model of hyperbolic space. It is a space of constant negative curvature $-1/R^2$. The 1 in the upper index refers to an enumeration of the different model spaces of hyperbolic geometry, and the for its dimension. A $2(2)$ corresponds to the Poincaré disk model, while $3(n)$ corresponds to the Poincaré half-space model of dimension $n.$

Preliminaries

In the definition above $\iota: \mathbf^_R \rightarrow \mathbf^$ is the inclusion map and the superscript star denotes the pullback. The present purpose is to describe this and similar operations as a preparation for the actual demonstration that $\mathbf^_R$ actually is a hyperbolic space.

Hyperbolic stereographic projection

In order to exhibit the metric, it is necessary to pull it back via a suitable ''parametrization''. A parametrization of a submanifold of a manifold is a map whose range is an open subset of . If has the same dimension as , a parametrization is just the inverse of a coordinate map . The parametrization to be used is the inverse of ''hyperbolic stereographic projection''. This is illustrated in the figure to the right for . It is instructive to compare to stereographic projection for spheres.

Stereographic projection and its inverse are given by
$\begin \sigma(\tau, \mathbf x) = \mathbf u &= \frac,\\ \sigma^(\mathbf u) = (\tau, \mathbf x) &= \left(R\frac, \frac\right), \end$
where, for simplicity, . The are coordinates on and the are coordinates on .

Pulling back the metric

One has
$h_R^ = \eta, _ = \left(dx^1\right)^2 + \cdots + \left(dx^n\right)^2 - d\tau^2$
and the map
$\sigma^:\mathbf^n \rightarrow \mathbf_R^;\quad \sigma^(\mathbf) = (\tau(\mathbf),\, \mathbf(\mathbf)) = \left(R\frac,\, \frac\right).$

The pulled back metric can be obtained by straightforward methods of calculus;
$\left.\left(\sigma^\right)^* \eta\_ = \left(dx^1(\mathbf u)\right)^2 + \cdots + \left(dx^n(\mathbf u)\right)^2 - \left(d\tau(\mathbf u)\right)^2.$

One computes according to the standard rules for computing differentials (though one is really computing the rigorously defined exterior derivatives),
$\begin dx^1(\mathbf u) &= d\left(\frac\right) = \frac\fracdu^1 + \cdots + \frac\fracdu^n + \frac\fracd\tau,\\ &\ \ \vdots\\ dx^n(\mathbf u) &= d\left(\frac\right) = \cdots,\\ d\tau(\mathbf u) &= d\left(R\frac\right) = \cdots, \end$
and substitutes the results into the right hand side. This yields
$\left(\sigma^\right)^* h_R^ = \frac \equiv h_R^.$

This last equation shows that the metric on the ball is identical to the Riemannian metric in the Poincaré ball model, another standard model of hyperbolic geometry.

See also

* Hyperbolic quaternion
* Hyperspace
* Introduction to the mathematics of general relativity
* Minkowski plane

Remarks

Notes

References

*
*
*
* Giulini D The rich structure of Minkowski space, https://arxiv.org/abs/0802.4345v1.
*
*
*
*
*
*
** Published translation:
** Wikisource translation: The Fundamental Equations for Electromagnetic Processes in Moving Bodies
* Various English translations on Wikisource: Space and Time.
* .
*
*
*
* Wikisource translation: On the Dynamics of the Electron
* Robb A A: Optical Geometry of Motion; a New View of the Theory of Relativity Cambridge 1911, (Heffers). http://www.archive.org/details/opticalgeometryoOOrobbrich.
* Robb A A: Geometry of Time and Space, 1936 Cambridge Univ Press http://www.archive.org/details/geometryoftimean032218mbp.
*
*
*
* .

External links

* visualizing Minkowski space in the context of special relativity.

The Geometry of Special Relativity: The Minkowski Space – Time Light Cone

Minkowski space
at PhilPapers

{{DEFAULTSORT:Minkowski Space
Equations of physics
Geometry

Lorentzian manifolds
Special relativity
Exact solutions in general relativity
Hermann Minkowski