|
Standard Gravitational Parameter
The standard gravitational parameter ''μ'' of a celestial body is the product of the gravitational constant ''G'' and the mass ''M'' of that body. For two bodies, the parameter may be expressed as , or as when one body is much larger than the other: \mu=G(M+m)\approx GM . For several objects in the Solar System, the value of ''μ'' is known to greater accuracy than either ''G'' or ''M''. The SI unit of the standard gravitational parameter is . However, the unit is frequently used in the scientific literature and in spacecraft navigation. Definition Small body orbiting a central body The central body in an orbital system can be defined as the one whose mass (''M'') is much larger than the mass of the orbiting body (''m''), or . This approximation is standard for planets orbiting the Sun or most moons and greatly simplifies equations. Under Newton's law of universal gravitation, if the distance between the bodies is ''r'', the force exerted on the smaller body is: F = ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mercury (planet)
Mercury is the first planet from the Sun. It is a rocky planet with a trace atmosphere. While it is the List of Solar System objects by size, smallest and least massive planet of the Solar System, its surface gravity is slightly higher than that of Mars. The surface of Mercury is similar to Earth's Moon, heavily Impact crater, cratered, with expansive rupes system, generated from thrust faults, and bright ray systems, formed by ejecta. Its largest crater, Caloris Planitia, has a diameter of , which is about one-third the diameter of the planet (). Being the most inferior planet, inferior orbiting planet it appears in Earth's sky, always close to the Sun, either as a "morning star" or an "evening star". It stays most of the time the closest to all other planets and is the planet with the highest delta-v needed to travel to from all other planets of the Solar System. Mercury's sidereal year (88.0 Earth days) and sidereal day (58.65 Earth days) are in a 3:2 ratio. This relation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kilometre
The kilometre (SI symbol: km; or ), spelt kilometer in American English, American and Philippine English, is a unit of length in the International System of Units (SI), equal to one thousand metres (kilo- being the SI prefix for ). It is the preferred measurement unit to express distances between geographical places on land in most of the world; notable exceptions are the United States and the United Kingdom where the statute mile is used. Pronunciation There are two common pronunciations for the word. # # The first pronunciation follows a pattern in English whereby SI units are pronounced with the stress on the first syllable (as in kilogram, kilojoule and kilohertz) and the pronunciation of the actual base unit does not change irrespective of the prefix (as in centimetre, millimetre, nanometre and so on). It is generally preferred by the British Broadcasting Corporation (BBC), the Canadian Broadcasting Corporation (CBC), and the Australian Broadcasting Corporation (ABC) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parabolic Trajectory
In astrodynamics or celestial mechanics a parabolic trajectory is a Kepler orbit with the Orbital eccentricity, eccentricity equal to 1 and is an unbound orbit that is exactly on the border between elliptical and hyperbolic. When moving away from the source it is called an escape orbit, otherwise a capture orbit. It is also sometimes referred to as a C3 = 0 orbit (see Characteristic energy). Under standard assumptions a body traveling along an escape orbit will coast along a Parabola, parabolic trajectory to infinity, with velocity relative to the central body tending to zero, and therefore will never return. Parabolic trajectories are minimum-energy escape trajectories, separating positive-characteristic energy, energy hyperbolic trajectory, hyperbolic trajectories from negative-energy elliptic orbits. Velocity The Kinetic energy, orbital velocity (v) of a body travelling along a parabolic trajectory can be computed as: :v = \sqrt where: *r is the radial distance of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kepler's Laws Of Planetary Motion
In astronomy, Kepler's laws of planetary motion, published by Johannes Kepler in 1609 (except the third law, which was fully published in 1619), describe the orbits of planets around the Sun. These laws replaced circular orbits and epicycles in the heliocentric theory of Nicolaus Copernicus with elliptical orbits and explained how planetary velocities vary. The three laws state that: # The orbit of a planet is an ellipse with the Sun at one of the two foci. # A line segment joining a planet and the Sun sweeps out equal areas during equal intervals of time. # The square of a planet's orbital period is proportional to the cube of the length of the semi-major axis of its orbit. The elliptical orbits of planets were indicated by calculations of the orbit of Mars. From this, Kepler inferred that other bodies in the Solar System, including those farther away from the Sun, also have elliptical orbits. The second law establishes that when a planet is closer to the Sun, it travels fa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Semi-major Axis
In geometry, the major axis of an ellipse is its longest diameter: a line segment that runs through the center and both foci, with ends at the two most widely separated points of the perimeter. The semi-major axis (major semiaxis) is the longest semidiameter or one half of the major axis, and thus runs from the centre, through a focus, and to the perimeter. The semi-minor axis (minor semiaxis) of an ellipse or hyperbola is a line segment that is at right angles with the semi-major axis and has one end at the center of the conic section. For the special case of a circle, the lengths of the semi-axes are both equal to the radius of the circle. The length of the semi-major axis of an ellipse is related to the semi-minor axis's length through the eccentricity and the semi-latus rectum \ell, as follows: The semi-major axis of a hyperbola is, depending on the convention, plus or minus one half of the distance between the two branches. Thus it is the distance from the ce ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
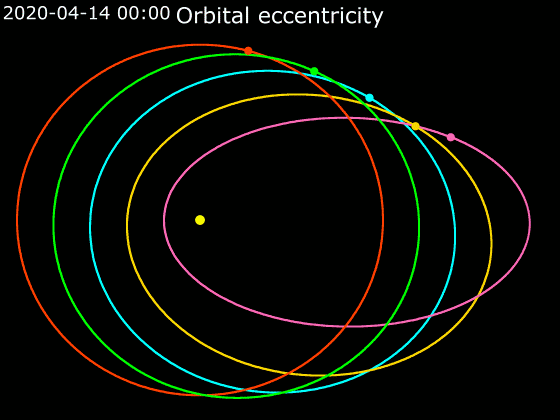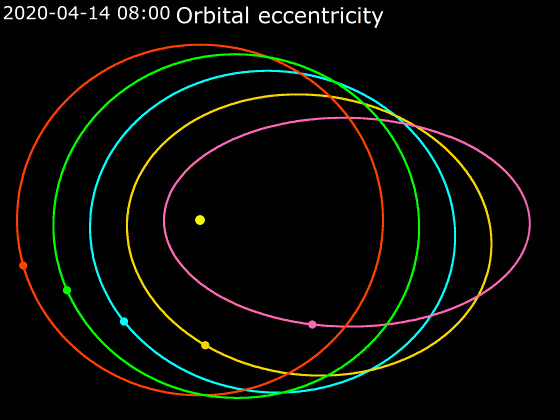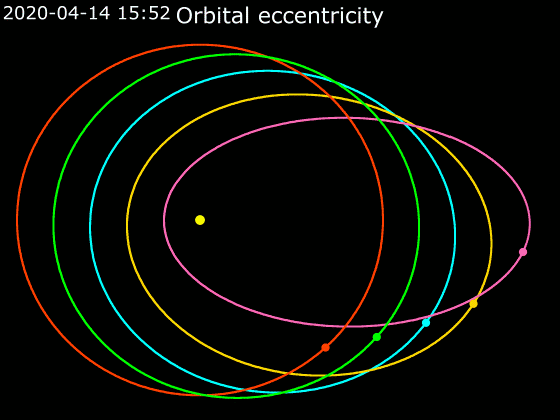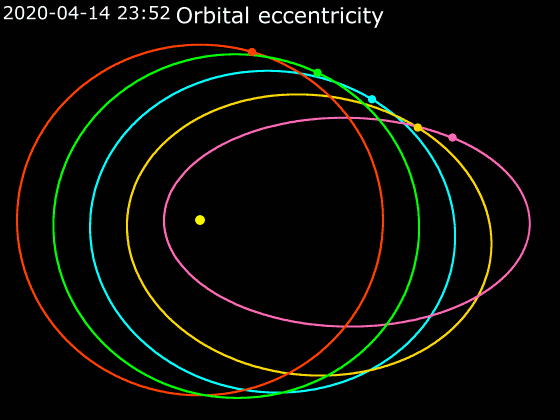
Elliptic Orbit
In astrodynamics or celestial mechanics, an elliptical orbit or eccentric orbit is an orbit with an eccentricity of less than 1; this includes the special case of a circular orbit, with eccentricity equal to 0. Some orbits have been referred to as "elongated orbits" if the eccentricity is "high" but that is not an explanatory term. For the simple two body problem, all orbits are ellipses. In a gravitational two-body problem, both bodies follow similar elliptical orbits with the same orbital period around their common barycenter. The relative position of one body with respect to the other also follows an elliptic orbit. Examples of elliptic orbits include Hohmann transfer orbits, Molniya orbits, and tundra orbits. Velocity Under standard assumptions, no other forces acting except two spherically symmetrical bodies (m_1) and (m_2), the orbital speed (v\,) of one body traveling along an elliptical orbit can be computed from the vis-viva equation as: :v = \sqrt where: * ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orbital Period
The orbital period (also revolution period) is the amount of time a given astronomical object takes to complete one orbit around another object. In astronomy, it usually applies to planets or asteroids orbiting the Sun, moons orbiting planets, exoplanets orbiting other stars, or binary stars. It may also refer to the time it takes a satellite orbiting a planet or moon to complete one orbit. For celestial objects in general, the orbital period is determined by a 360° revolution of one body around its primary, ''e.g.'' Earth around the Sun. Periods in astronomy are expressed in units of time, usually hours, days, or years. Its reciprocal is the orbital frequency, a kind of revolution frequency, in units of hertz. Small body orbiting a central body According to Kepler's Third Law, the orbital period ''T'' of two point masses orbiting each other in a circular or elliptic orbit is: :T = 2\pi\sqrt where: * ''a'' is the orbit's semi-major axis * ''G'' is the gravitationa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Angular Speed
In physics, angular frequency (symbol ''ω''), also called angular speed and angular rate, is a scalar measure of the angle rate (the angle per unit time) or the temporal rate of change of the phase argument of a sinusoidal waveform or sine function (for example, in oscillations and waves). Angular frequency (or angular speed) is the magnitude of the pseudovector quantity ''angular velocity''. (UP1) Angular frequency can be obtained multiplying ''rotational frequency'', ''ν'' (or ordinary ''frequency'', ''f'') by a full turn (2 radians): . It can also be formulated as , the instantaneous rate of change of the angular displacement, ''θ'', with respect to time, ''t''. (11 pages) Unit In SI |
Orbital Speed
In gravitationally bound systems, the orbital speed of an astronomical body or object (e.g. planet, moon, artificial satellite, spacecraft, or star) is the speed at which it orbits around either the barycenter (the combined center of mass) or, if one body is much more massive than the other bodies of the system combined, its speed relative to the center of mass of the most massive body. The term can be used to refer to either the mean orbital speed (i.e. the average speed over an entire orbit) or its instantaneous speed at a particular point in its orbit. The maximum (instantaneous) orbital speed occurs at periapsis (perigee, perihelion, etc.), while the minimum speed for objects in closed orbits occurs at apoapsis (apogee, aphelion, etc.). In ideal two-body systems, objects in open orbits continue to slow down forever as their distance to the barycenter increases. When a system approximates a two-body system, instantaneous orbital speed at a given point of the orbit can b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Radius
In classical geometry, a radius (: radii or radiuses) of a circle or sphere is any of the line segments from its Centre (geometry), center to its perimeter, and in more modern usage, it is also their length. The radius of a regular polygon is the line segment or distance from its center to any of its Vertex (geometry), vertices. The name comes from the Latin ''radius'', meaning ray but also the spoke of a chariot wheel.Definition of Radius at dictionary.reference.com. Accessed on 2009-08-08. The typical abbreviation and mathematical symbol for radius is ''R'' or ''r''. By extension, the diameter ''D'' is defined as twice the radius:Definition of radius at mathwords.com. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Centripetal Force
Centripetal force (from Latin ''centrum'', "center" and ''petere'', "to seek") is the force that makes a body follow a curved trajectory, path. The direction of the centripetal force is always orthogonality, orthogonal to the motion of the body and towards the fixed point of the instantaneous osculating circle, center of curvature of the path. Isaac Newton coined the term, describing it as "a force by which bodies are drawn or impelled, or in any way tend, towards a point as to a centre". In Newtonian mechanics, gravity provides the centripetal force causing astronomical orbits. One common example involving centripetal force is the case in which a body moves with uniform speed along a circular path. The centripetal force is directed at right angles to the motion and also along the radius towards the centre of the circular path. The mathematical description was derived in 1659 by the Dutch physicist Christiaan Huygens. Formula From the kinematics of curved motion it is known ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circular Orbit
A circular orbit is an orbit with a fixed distance around the barycenter; that is, in the shape of a circle. In this case, not only the distance, but also the speed, angular speed, Potential energy, potential and kinetic energy are constant. There is no periapsis or apoapsis. This orbit has no Radial orbit, radial version. Listed below is a circular orbit in astrodynamics or celestial mechanics under standard assumptions. Here the centripetal force is the gravitational force, and the axis mentioned above is the line through the Center of mass, center of the central mass perpendicular to the orbital plane. Circular acceleration :wikt:transverse, Transverse acceleration (perpendicular to velocity) causes a change in direction. If it is constant in magnitude and changing in direction with the velocity, circular motion ensues. Taking two derivatives of the particle's coordinates concerning time gives the centripetal acceleration : a\, = \frac \, = where: *v\, is Kinetic e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |