|
Spherical Conic
In mathematics, a spherical conic or sphero-conic is a curve on the sphere, the intersection of the sphere with a concentric elliptic cone. It is the spherical analog of a conic section (ellipse, parabola, or hyperbola) in the plane, and as in the planar case, a spherical conic can be defined as the locus (mathematics), locus of points the sum or difference of whose great-circle distances to two focus (geometry), foci is constant. By taking the antipodal point to one focus, every spherical ellipse is also a spherical hyperbola, and vice versa. As a space curve, a spherical conic is a quartic function, quartic, though its orthogonal projections in three Principal axis theorem, principal axes are planar conics. Like planar conics, spherical conics also satisfy a "reflection property": the great-circle arcs from the two foci to any point on the conic have the tangent and normal to the conic at that point as their angle bisectors. Many theorems about conics in the plane extend to sp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ellipse
In mathematics, an ellipse is a plane curve surrounding two focus (geometry), focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. It generalizes a circle, which is the special type of ellipse in which the two focal points are the same. The elongation of an ellipse is measured by its eccentricity (mathematics), eccentricity e, a number ranging from e = 0 (the Limiting case (mathematics), limiting case of a circle) to e = 1 (the limiting case of infinite elongation, no longer an ellipse but a parabola). An ellipse has a simple algebraic solution for its area, but for Perimeter of an ellipse, its perimeter (also known as circumference), Integral, integration is required to obtain an exact solution. The largest and smallest diameters of an ellipse, also known as its width and height, are typically denoted and . An ellipse has four extreme points: two ''Vertex (geometry), vertices'' at the endpoints of the major axis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Solid Geometry
Euclidean (or, less commonly, Euclidian) is an adjective derived from the name of Euclid, an ancient Greek mathematician. Geometry *Euclidean space, the two-dimensional plane and three-dimensional space of Euclidean geometry as well as their higher dimensional generalizations *Euclidean geometry, the study of the properties of Euclidean spaces *Non-Euclidean geometry, systems of points, lines, and planes analogous to Euclidean geometry but without uniquely determined parallel lines *Euclidean distance, the distance between pairs of points in Euclidean spaces *Euclidean ball, the set of points within some fixed distance from a center point Number theory *Euclidean division, the division which produces a quotient and a remainder *Euclidean algorithm, a method for finding greatest common divisors *Extended Euclidean algorithm, a method for solving the Diophantine equation ''ax'' + ''by'' = ''d'' where ''d'' is the greatest common divisor of ''a'' and ''b'' *Euclid's lemma: if a p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spherical Geometry
300px, A sphere with a spherical triangle on it. Spherical geometry or spherics () is the geometry of the two-dimensional surface of a sphere or the -dimensional surface of higher dimensional spheres. Long studied for its practical applications to astronomy, navigation, and geodesy, spherical geometry and the metrical tools of spherical trigonometry are in many respects analogous to Euclidean plane geometry and trigonometry, but also have some important differences. The sphere can be studied either ''extrinsically'' as a surface embedded in 3-dimensional Euclidean space (part of the study of solid geometry), or ''intrinsically'' using methods that only involve the surface itself without reference to any surrounding space. Principles In plane (Euclidean) geometry, the basic concepts are points and (straight) lines. In spherical geometry, the basic concepts are points and great circles. However, two great circles on a plane intersect in two antipodal points, unlike coplan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spherical Curves
A sphere (from Greek , ) is a surface analogous to the circle, a curve. In solid geometry, a sphere is the set of points that are all at the same distance from a given point in three-dimensional space.. That given point is the ''center'' of the sphere, and the distance is the sphere's ''radius''. The earliest known mentions of spheres appear in the work of the ancient Greek mathematicians. The sphere is a fundamental surface in many fields of mathematics. Spheres and nearly-spherical shapes also appear in nature and industry. Bubbles such as soap bubbles take a spherical shape in equilibrium. The Earth is often approximated as a sphere in geography, and the celestial sphere is an important concept in astronomy. Manufactured items including pressure vessels and most curved mirrors and lenses are based on spheres. Spheres roll smoothly in any direction, so most balls used in sports and toys are spherical, as are ball bearings. Basic terminology As mentioned earlie ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conic Sections
A conic section, conic or a quadratic curve is a curve obtained from a Conical surface, cone's surface intersecting a plane (mathematics), plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, though it was sometimes considered a fourth type. The Greek mathematics, ancient Greek mathematicians studied conic sections, culminating around 200 BC with Apollonius of Perga's systematic work on their properties. The conic sections in the Euclidean plane have various distinguishing properties, many of which can be used as alternative definitions. One such property defines a non-circular conic to be the set (mathematics), set of those points whose distances to some particular point, called a ''Focus (geometry), focus'', and some particular line, called a ''directrix'', are in a fixed ratio, called the ''Eccentricity (mathematics), eccentricity''. The type of conic is determined by the value of the ec ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
TU Wien
TU Wien () is a public research university in Vienna, Austria. The university's teaching and research are focused on engineering, computer science, and natural sciences. It currently has about 28,100 students (29% women), eight faculties, and about 5,000 staff members (3,800 academics). History The institution was founded in 1815 by Emperor Francis I of Austria as the '' k.k. Polytechnisches Institut'' (). The first rector was Johann Joseph von Prechtl. It was renamed the ''Technische Hochschule'' () in 1872. In 1975, it was renamed ''Technische Universität Wien'' (). Academic reputation As a university of technology, TU Wien covers a wide spectrum of scientific concepts from abstract pure research and the fundamental principles of science to applied technological research and partnership with industry. TU Wien is ranked #190 by the QS World University Ranking, #406 by the Center of World University Rankings, and it is positioned among the best 251-300 higher education ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbolic Navigation
Hyperbolic navigation is a class of radio navigation systems in which a navigation receiver instrument is used to determine location based on the difference in timing of radio waves received from radio navigation beacon transmitters. Such systems rely on the ability of two widely separated stations to broadcast a signal that is highly correlated in time. Typical systems broadcast either short pulses at the same time, or continual signals that are identical in phase. A receiver located at the midpoint between the two stations will receive the signals at the same time or have identical phase, but at any other location the signal from the closer station will be received first or have a different phase. Determining the location of a receiver requires that the two synchronized stations be tuned in at the same time so the signals can be compared. This reveals a ''difference'' in time, corresponding to a relative distance closer to one station or the other. Plotting all the locations ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
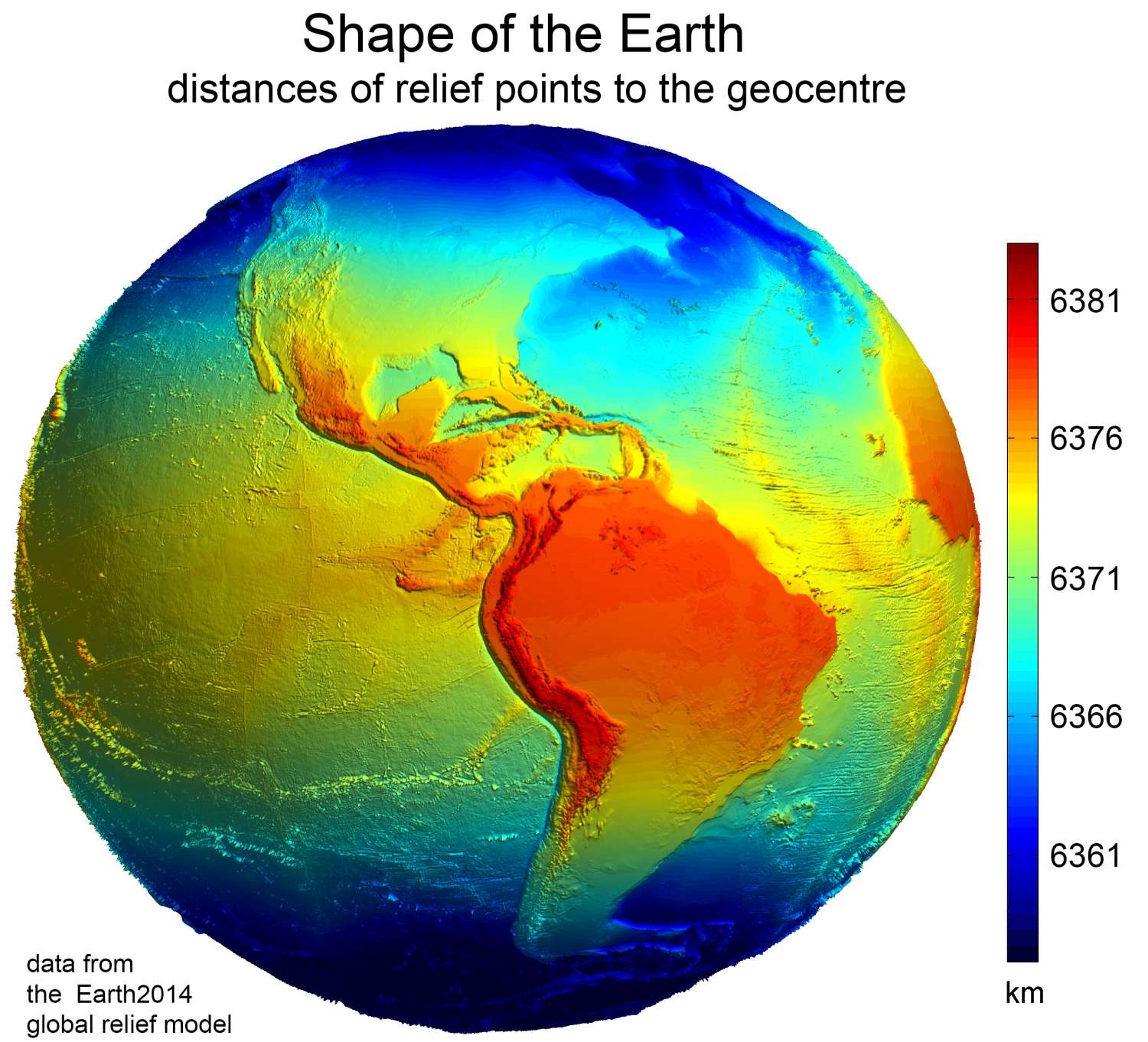
Osculating Sphere
In geodesy, the figure of the Earth is the size and shape used to model planet Earth. The kind of figure depends on application, including the precision needed for the model. A spherical Earth is a well-known historical approximation that is satisfactory for geography, astronomy and many other purposes. Several models with greater accuracy (including ellipsoid) have been developed so that coordinate systems can serve the precise needs of navigation, surveying, cadastre, land use, and various other concerns. Motivation Earth's topographic surface is apparent with its variety of land forms and water areas. This topographic surface is generally the concern of topographers, hydrographers, and geophysicists. While it is the surface on which Earth measurements are made, mathematically modeling it while taking the irregularities into account would be extremely complicated. The Pythagorean concept of a spherical Earth offers a simple surface that is easy to deal with mathematically ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kepler Problem
In classical mechanics, the Kepler problem is a special case of the two-body problem, in which the two bodies interact by a central force that varies in strength as the inverse square of the distance between them. The force may be either attractive or repulsive. The problem is to find the position or speed of the two bodies over time given their masses, positions, and velocities. Using classical mechanics, the solution can be expressed as a Kepler orbit using six orbital elements. The Kepler problem is named after Johannes Kepler, who proposed Kepler's laws of planetary motion (which are part of classical mechanics and solved the problem for the orbits of the planets) and investigated the types of forces that would result in orbits obeying those laws (called ''Kepler's inverse problem''). For a discussion of the Kepler problem specific to radial orbits, see Radial trajectory. General relativity provides more accurate solutions to the two-body problem, especially in stron ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elliptic Coordinate System
In geometry, the elliptic coordinate system is a two-dimensional orthogonal coordinate system in which the coordinate lines are confocal ellipses and hyperbolae. The two foci F_ and F_ are generally taken to be fixed at -a and +a, respectively, on the x-axis of the Cartesian coordinate system. Basic definition The most common definition of elliptic coordinates (\mu, \nu) is :\begin x &= a \ \cosh \mu \ \cos \nu \\ y &= a \ \sinh \mu \ \sin \nu \end where \mu is a nonnegative real number and \nu \in , 2\pi On the complex plane, an equivalent relationship is :x + iy = a \ \cosh(\mu + i\nu) These definitions correspond to ellipses and hyperbolae. The trigonometric identity :\frac + \frac = \cos^ \nu + \sin^ \nu = 1 shows that curves of constant \mu form ellipses, whereas the hyperbolic trigonometric identity :\frac - \frac = \cosh^ \mu - \sinh^ \mu = 1 shows that curves of constant \nu form hyperbolae. Scale factors In an orthogonal coordinate system the lengths of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |