|
SQIsign
SQIsign is a post-quantum signature scheme submitted to first round of the post-quantum standardisation process. It is based around a proof of knowledge of an elliptic curve endomorphism that can be transformed to a signature scheme using the Fiat–Shamir transform. It promises small key sizes between 64 and 128 bytes and small signature sizes between 177 and 335 bytes, which outperforms other post-quantum signature schemes that have a trade-off between signature and key sizes. SQIsign, however, has higher signing and verification times. The original paper concluded that their C implementation takes 0.6 s for key generation, 2.5 s for a sign operation and 0.05 s or 50 ms for a verification operation. These times have been improved with new variations like SQIsign-east. The name stands for "Short Quaternion and Isogeny Signature" as it makes use of isogenies and quaternions. Security SQIsign's security relies on the hardness of the endomorphism ring pro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
NIST Post-Quantum Cryptography Standardization
Post-Quantum Cryptography Standardization is a program and competition by NIST to update their standards to include post-quantum cryptography. It was announced at PQCrypto 2016. 23 signature schemes and 59 encryption/ KEM schemes were submitted by the initial submission deadline at the end of 2017 of which 69 total were deemed complete and proper and participated in the first round. Seven of these, of which 3 are signature schemes, have advanced to the third round, which was announced on July 22, 2020. On August 13, 2024, NIST released final versions of the first three Post Quantum Crypto Standards: FIPS 203, FIPS 204, and FIPS 205.NIST Releases First 3 Finalized Post-Quantum Encryption Standards NIST, August 13, 2024 [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Post-quantum Cryptography
Post-quantum cryptography (PQC), sometimes referred to as quantum-proof, quantum-safe, or quantum-resistant, is the development of cryptographic algorithms (usually public-key algorithms) that are currently thought to be secure against a cryptanalytic attack by a quantum computer. Most widely-used public-key algorithms rely on the difficulty of one of three mathematical problems: the integer factorization problem, the discrete logarithm problem or the elliptic-curve discrete logarithm problem. All of these problems could be easily solved on a sufficiently powerful quantum computer running Shor's algorithm or possibly alternatives. As of 2024, quantum computers lack the processing power to break widely used cryptographic algorithms; however, because of the length of time required for migration to quantum-safe cryptography, cryptographers are already designing new algorithms to prepare for Y2Q or Q-Day, the day when current algorithms will be vulnerable to quantum computin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
NIST
The National Institute of Standards and Technology (NIST) is an agency of the United States Department of Commerce whose mission is to promote American innovation and industrial competitiveness. NIST's activities are organized into physical science laboratory programs that include nanoscale science and technology, engineering, information technology, neutron research, material measurement, and physical measurement. From 1901 to 1988, the agency was named the National Bureau of Standards. History Background The Articles of Confederation, ratified by the colonies in 1781, provided: The United States in Congress assembled shall also have the sole and exclusive right and power of regulating the alloy and value of coin struck by their own authority, or by that of the respective states—fixing the standards of weights and measures throughout the United States. Article 1, section 8, of the Constitution of the United States, ratified in 1789, granted these powers to the new Co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
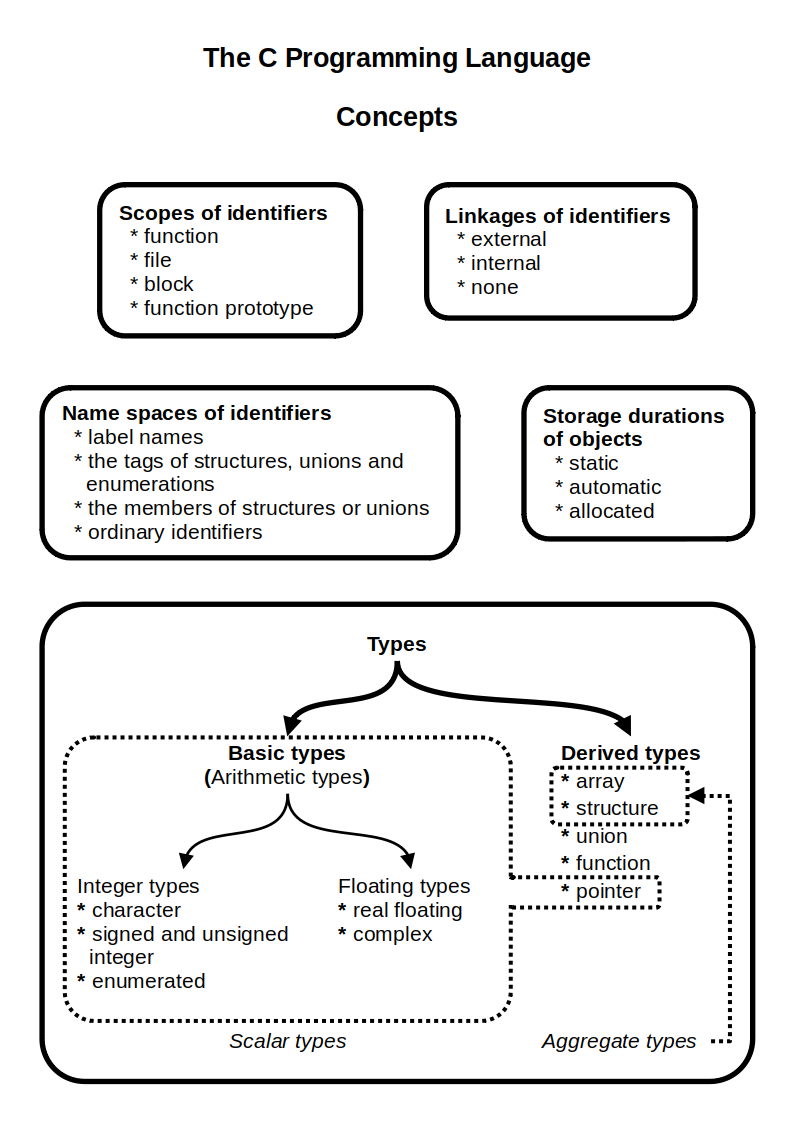
C (programming Language)
C (''pronounced'' '' – like the letter c'') is a general-purpose programming language. It was created in the 1970s by Dennis Ritchie and remains very widely used and influential. By design, C's features cleanly reflect the capabilities of the targeted Central processing unit, CPUs. It has found lasting use in operating systems code (especially in Kernel (operating system), kernels), device drivers, and protocol stacks, but its use in application software has been decreasing. C is commonly used on computer architectures that range from the largest supercomputers to the smallest microcontrollers and embedded systems. A successor to the programming language B (programming language), B, C was originally developed at Bell Labs by Ritchie between 1972 and 1973 to construct utilities running on Unix. It was applied to re-implementing the kernel of the Unix operating system. During the 1980s, C gradually gained popularity. It has become one of the most widely used programming langu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
GitHub
GitHub () is a Proprietary software, proprietary developer platform that allows developers to create, store, manage, and share their code. It uses Git to provide distributed version control and GitHub itself provides access control, bug tracking system, bug tracking, software feature requests, task management, continuous integration, and wikis for every project. Headquartered in California, GitHub, Inc. has been a subsidiary of Microsoft since 2018. It is commonly used to host open source software development projects. GitHub reported having over 100 million developers and more than 420 million Repository (version control), repositories, including at least 28 million public repositories. It is the world's largest source code host Over five billion developer contributions were made to more than 500 million open source projects in 2024. About Founding The development of the GitHub platform began on October 19, 2005. The site was launched in April 2008 by Tom ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
SIDH
Supersingular isogeny Diffie–Hellman key exchange (SIDH or SIKE) is an insecure proposal for a post-quantum cryptographic algorithm to establish a secret key between two parties over an untrusted communications channel. It is analogous to the Diffie–Hellman key exchange, but is based on walks in a supersingular isogeny graph and was designed to resist cryptanalytic attack by an adversary in possession of a quantum computer. Before it was broken, SIDH boasted one of the smallest key sizes of all post-quantum key exchanges; with compression, SIDH used 2688-bit public keys at a 128-bit quantum security level. SIDH also distinguishes itself from similar systems such as NTRU and Ring-LWE by supporting perfect forward secrecy, a property that prevents compromised long-term keys from compromising the confidentiality of old communication sessions. These properties seemed to make SIDH a natural candidate to replace Diffie–Hellman (DHE) and elliptic curve Diffie–Hellma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nothing-up-my-sleeve Number
In cryptography, nothing-up-my-sleeve numbers are any numbers which, by their construction, are above suspicion of hidden properties. They are used in creating cryptographic functions such as hashes and ciphers. These algorithms often need randomized constants for mixing or initialization purposes. The cryptographer may wish to pick these values in a way that demonstrates the constants were not selected for a nefarious purpose, for example, to create a backdoor to the algorithm. These fears can be allayed by using numbers created in a way that leaves little room for adjustment. An example would be the use of initial digits from the number as the constants. Using digits of millions of places after the decimal point would not be considered trustworthy because the algorithm designer might have selected that starting point because it created a secret weakness the designer could later exploit—though even with natural-seeming selections, enough entropy exists in the possible choic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quaternion
In mathematics, the quaternion number system extends the complex numbers. Quaternions were first described by the Irish mathematician William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space. The algebra of quaternions is often denoted by (for ''Hamilton''), or in blackboard bold by \mathbb H. Quaternions are not a field, because multiplication of quaternions is not, in general, commutative. Quaternions provide a definition of the quotient of two vectors in a three-dimensional space. Quaternions are generally represented in the form a + b\,\mathbf i + c\,\mathbf j +d\,\mathbf k, where the coefficients , , , are real numbers, and , are the ''basis vectors'' or ''basis elements''. Quaternions are used in pure mathematics, but also have practical uses in applied mathematics, particularly for calculations involving three-dimensional rotations, such as in three-dimensional computer graphics, computer vision, robotics, magnetic resonance i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isogeny
In mathematics, particularly in algebraic geometry, an isogeny is a morphism of algebraic groups (also known as group varieties) that is surjective and has a finite kernel. If the groups are abelian varieties, then any morphism of the underlying algebraic varieties which is surjective with finite fibres is automatically an isogeny, provided that . Such an isogeny then provides a group homomorphism between the groups of -valued points of and , for any field over which is defined. The terms "isogeny" and "isogenous" come from the Greek word ισογενη-ς, meaning "equal in kind or nature". The term "isogeny" was introduced by Weil; before this, the term "isomorphism" was somewhat confusingly used for what is now called an isogeny. Degree of isogeny Let be isogeny between two algebraic groups. This mapping induces a pullback mapping between their rational function fields. Since the mapping is nontrivial, it is a field embedding and \operatorname f^* is a subfield of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Endomorphism Ring
In mathematics, the endomorphisms of an abelian group ''X'' form a ring. This ring is called the endomorphism ring of ''X'', denoted by End(''X''); the set of all homomorphisms of ''X'' into itself. Addition of endomorphisms arises naturally in a pointwise manner and multiplication via endomorphism composition. Using these operations, the set of endomorphisms of an abelian group forms a (unital) ring, with the zero map 0: x \mapsto 0 as additive identity and the identity map 1: x \mapsto x as multiplicative identity. The functions involved are restricted to what is defined as a homomorphism in the context, which depends upon the category of the object under consideration. The endomorphism ring consequently encodes several internal properties of the object. As the endomorphism ring is often an algebra over some ring ''R,'' this may also be called the endomorphism algebra. An abelian group is the same thing as a module over the ring of integers, which is the initial object ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fiat–Shamir Heuristic
In cryptography, the Fiat–Shamir heuristic is a technique for taking an interactive proof of knowledge and creating a digital signature based on it. This way, some fact (for example, knowledge of a certain secret number) can be publicly proven without revealing underlying information. The technique is due to Amos Fiat and Adi Shamir (1986). For the method to work, the original interactive proof must have the property of being public-coin, i.e. verifier's random coins are made public throughout the proof protocol. Overview The heuristic was originally presented without a proof of security; later, Pointcheval and Stern proved its security against chosen message attacks in the ''random oracle model'', that is, assuming random oracles exist. This result was generalized to the quantum-accessible random oracle (QROM) by Don, Fehr, Majenz and Schaffner, and concurrently by Liu and Zhandry. In the case that random oracles do not exist, the Fiat–Shamir heuristic has been proven ins ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Supersingular Isogeny Graph
In mathematics, the supersingular isogeny graphs are a class of expander graphs that arise in computational number theory and have been applied in elliptic-curve cryptography. Their vertices represent supersingular elliptic curves over finite fields and their edges represent isogenies between curves. Definition and properties A supersingular isogeny graph is determined by choosing a large prime number p and a small prime number \ell, and considering the class of all supersingular elliptic curves defined over the finite field \mathbb_. There are approximately (p+1)/12 such curves, each two of which can be related by isogenies. The vertices in the supersingular isogeny graph represent these curves (or more concretely, their -invariants, elements of \mathbb_) and the edges represent isogenies of degree \ell between two curves. The supersingular isogeny graphs are \ell+1-regular graphs, meaning that each vertex has exactly \ell+1 neighbors. They were proven by Pizer to be Ramanujan gr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |