|
SIDH
Supersingular isogeny Diffie–Hellman key exchange (SIDH or SIKE) is an insecure proposal for a post-quantum cryptographic algorithm to establish a secret key between two parties over an untrusted communications channel. It is analogous to the Diffie–Hellman key exchange, but is based on walks in a supersingular isogeny graph and was designed to resist cryptanalytic attack by an adversary in possession of a quantum computer. Before it was broken, SIDH boasted one of the smallest key sizes of all post-quantum key exchanges; with compression, SIDH used 2688-bit public keys at a 128-bit quantum security level. SIDH also distinguishes itself from similar systems such as NTRU and Ring-LWE by supporting perfect forward secrecy, a property that prevents compromised long-term keys from compromising the confidentiality of old communication sessions. These properties seemed to make SIDH a natural candidate to replace Diffie–Hellman (DHE) and elliptic curve Diffie–Hellma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Post-quantum Cryptography
Post-quantum cryptography (PQC), sometimes referred to as quantum-proof, quantum-safe, or quantum-resistant, is the development of cryptographic algorithms (usually public-key algorithms) that are currently thought to be secure against a cryptanalytic attack by a quantum computer. Most widely-used public-key algorithms rely on the difficulty of one of three mathematical problems: the integer factorization problem, the discrete logarithm problem or the elliptic-curve discrete logarithm problem. All of these problems could be easily solved on a sufficiently powerful quantum computer running Shor's algorithm or possibly alternatives. As of 2024, quantum computers lack the processing power to break widely used cryptographic algorithms; however, because of the length of time required for migration to quantum-safe cryptography, cryptographers are already designing new algorithms to prepare for Y2Q or Q-Day, the day when current algorithms will be vulnerable to quantum computin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
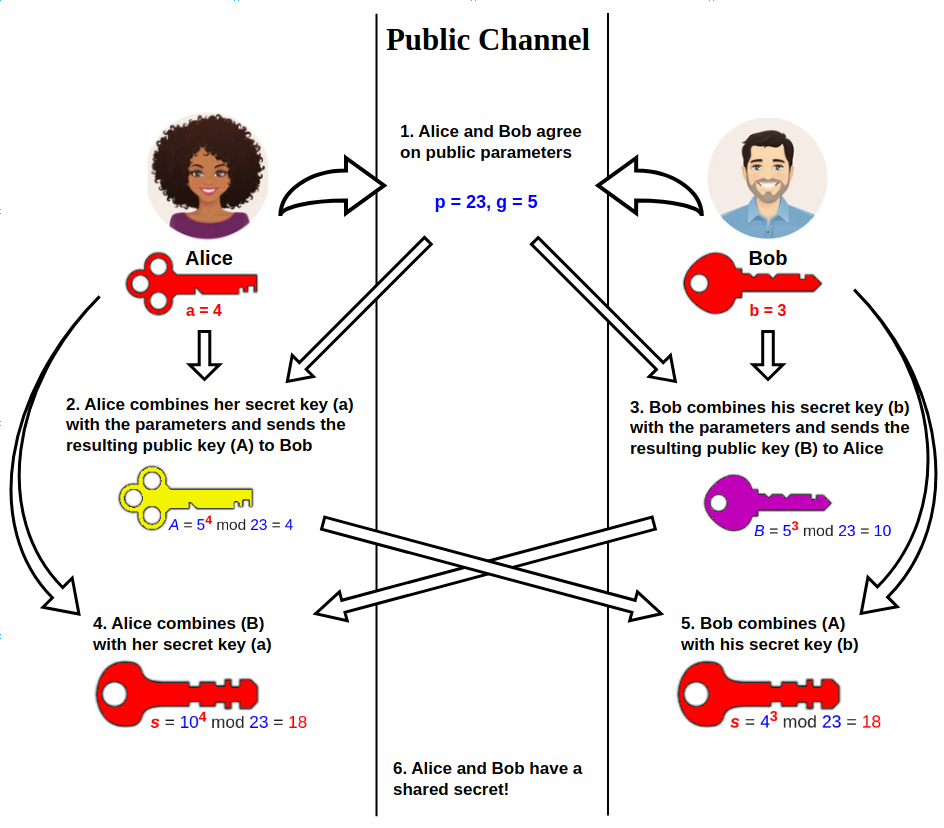
Diffie–Hellman Key Exchange
Diffie–Hellman (DH) key exchangeSynonyms of Diffie–Hellman key exchange include: * Diffie–Hellman–Merkle key exchange * Diffie–Hellman key agreement * Diffie–Hellman key establishment * Diffie–Hellman key negotiation * Exponential key exchange * Diffie–Hellman protocol * Diffie–Hellman handshake is a mathematical method of securely generating a symmetric cryptographic key over a public channel and was one of the first public-key protocols as conceived by Ralph Merkle and named after Whitfield Diffie and Martin Hellman. DH is one of the earliest practical examples of public key exchange implemented within the field of cryptography. Published in 1976 by Diffie and Hellman, this is the earliest publicly known work that proposed the idea of a private key and a corresponding public key. Traditionally, secure encrypted communication between two parties required that they first exchange keys by some secure physical means, such as paper key lists transported by a tr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elliptic Curve Cryptography
Elliptic-curve cryptography (ECC) is an approach to public-key cryptography based on the algebraic structure of elliptic curves over finite fields. ECC allows smaller keys to provide equivalent security, compared to cryptosystems based on modular exponentiation in Galois fields, such as the RSA cryptosystem and ElGamal cryptosystem. Elliptic curves are applicable for key agreement, digital signatures, pseudo-random generators and other tasks. Indirectly, they can be used for encryption by combining the key agreement with a symmetric encryption scheme. They are also used in several integer factorization algorithms that have applications in cryptography, such as Lenstra elliptic-curve factorization. History The use of elliptic curves in cryptography was suggested independently by Neal Koblitz and Victor S. Miller in 1985. Elliptic curve cryptography algorithms entered wide use in 2004 to 2005. In 1999, NIST recommended fifteen elliptic curves. Specifically, FIPS 186 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
General Number Field Sieve
In number theory, the general number field sieve (GNFS) is the most efficient classical algorithm known for factoring integers larger than . Heuristically, its complexity for factoring an integer (consisting of bits) is of the form : \begin & \exp\left(\left((64/9)^+o(1)\right)\left(\log n\right)^ \left(\log\log n\right)^\right) \\ pt= & L_n\left /3,(64/9)^\right\end in O and L-notations. It is a generalization of the special number field sieve: while the latter can only factor numbers of a certain special form, the general number field sieve can factor any number apart from prime powers (which are trivial to factor by taking roots). The principle of the number field sieve (both special and general) can be understood as an improvement to the simpler rational sieve or quadratic sieve. When using such algorithms to factor a large number , it is necessary to search for smooth numbers (i.e. numbers with small prime factors) of order . The size of these values is exponentia ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transport Layer Security
Transport Layer Security (TLS) is a cryptographic protocol designed to provide communications security over a computer network, such as the Internet. The protocol is widely used in applications such as email, instant messaging, and voice over IP, but its use in securing HTTPS remains the most publicly visible. The TLS protocol aims primarily to provide security, including privacy (confidentiality), integrity, and authenticity through the use of cryptography, such as the use of certificates, between two or more communicating computer applications. It runs in the presentation layer and is itself composed of two layers: the TLS record and the TLS handshake protocols. The closely related Datagram Transport Layer Security (DTLS) is a communications protocol that provides security to datagram-based applications. In technical writing, references to "(D)TLS" are often seen when it applies to both versions. TLS is a proposed Internet Engineering Task Force (IETF) standard, fir ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
ElGamal Signature Scheme
The ElGamal signature scheme is a digital signature scheme which is based on the difficulty of computing discrete logarithms. It was described by Taher Elgamal in 1985. (conference version appeared in CRYPTO'84, pp. 10–18) The ElGamal signature algorithm is rarely used in practice. A variant developed at the NSA and known as the Digital Signature Algorithm is much more widely used. There are several other variants. The ElGamal signature scheme must not be confused with ElGamal encryption which was also invented by Taher Elgamal. Overview The ElGamal signature scheme is a digital signature scheme based on the algebraic properties of modular exponentiation, together with the discrete logarithm problem. The algorithm uses a key pair consisting of a public key and a private key. The private key is used to generate a digital signature for a message, and such a signature can be verified by using the signer's corresponding public key. The digital signature provides message authenti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ed25519
In public-key cryptography, Edwards-curve Digital Signature Algorithm (EdDSA) is a digital signature scheme using a variant of Schnorr signature based on twisted Edwards curves. It is designed to be faster than existing digital signature schemes without sacrificing security. It was developed by a team including Daniel J. Bernstein, Niels Duif, Tanja Lange, Peter Schwabe, and Bo-Yin Yang. The reference implementation is public-domain software. Summary The following is a simplified description of EdDSA, ignoring details of encoding integers and curve points as bit strings; the full details are in the papers and RFC. An EdDSA signature scheme is a choice: * of finite field \mathbb_q over odd prime power q; * of elliptic curve E over \mathbb_q whose group E(\mathbb_q) of \mathbb_q-rational points has order \#E(\mathbb_q) = 2^c \ell, where \ell is a large prime and 2^c is called the cofactor; * of base point B \in E(\mathbb_q) with order \ell; and * of cryptographic hash functi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Curve25519
In cryptography, Curve25519 is an elliptic curve used in elliptic-curve cryptography (ECC) offering 128 bits of security (256-bit key size) and designed for use with the Elliptic-curve Diffie–Hellman (ECDH) key agreement scheme, first described and implemented by Daniel J. Bernstein. It is one of the fastest curves in ECC, and is not covered by any known patents. The reference implementation is public domain software. The original Curve25519 paper defined it as a Diffie–Hellman (DH) function. Bernstein has since proposed that the name Curve25519 be used for the underlying curve, and the name X25519 for the DH function. Mathematical properties The curve used is y^2 = x^3 + 486662x^2 + x, a Montgomery curve, over the prime field defined by the pseudo-Mersenne prime number 2^ - 19 (hence the numeric "" in the name), and it uses the base point x = 9. This point generates a cyclic subgroup whose order is the prime 2^ + 27742317777372353535851937790883648493. This subgroup has ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elliptic Curve DSA
In cryptography, the Elliptic Curve Digital Signature Algorithm (ECDSA) offers a variant of the Digital Signature Algorithm (DSA) which uses elliptic-curve cryptography. Key and signature sizes As with elliptic-curve cryptography in general, the bit size of the private key believed to be needed for ECDSA is about twice the size of the security level, in bits. For example, at a security level of 80 bits—meaning an attacker requires a maximum of about 2^ operations to find the private key—the size of an ECDSA private key would be 160 bits. On the other hand, the signature size is the same for both DSA and ECDSA: approximately 4 t bits, where t is the exponent in the formula 2^, that is, about 320 bits for a security level of 80 bits, which is equivalent to 2^ operations. Signature generation algorithm Suppose Alice wants to send a signed message to Bob. Initially, they must agree on the curve parameters (\textrm, G, n). In addition to the field and equation of the cu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elliptic Curve Diffie–Hellman
In mathematics, an ellipse is a plane curve surrounding two focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. It generalizes a circle, which is the special type of ellipse in which the two focal points are the same. The elongation of an ellipse is measured by its eccentricity e, a number ranging from e = 0 (the limiting case of a circle) to e = 1 (the limiting case of infinite elongation, no longer an ellipse but a parabola). An ellipse has a simple algebraic solution for its area, but for its perimeter (also known as circumference), integration is required to obtain an exact solution. The largest and smallest diameters of an ellipse, also known as its width and height, are typically denoted and . An ellipse has four extreme points: two '' vertices'' at the endpoints of the major axis and two ''co-vertices'' at the endpoints of the minor axis. Analytically, the equation of a standard ellipse centered at ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discrete Logarithm Problem
In mathematics, for given real numbers a and b, the logarithm \log_b(a) is a number x such that b^x=a. Analogously, in any group G, powers b^k can be defined for all integers k, and the discrete logarithm \log_b(a) is an integer k such that b^k=a. In arithmetic modulo an integer m, the more commonly used term is index: One can write k=\mathbb_b a \pmod (read "the index of a to the base b modulo m") for b^k \equiv a \pmod if b is a primitive root of m and \gcd(a,m)=1. Discrete logarithms are quickly computable in a few special cases. However, no efficient method is known for computing them in general. In cryptography, the computational complexity of the discrete logarithm problem, along with its application, was first proposed in the Diffie–Hellman problem. Several important algorithms in public-key cryptography, such as ElGamal, base their security on the hardness assumption that the discrete logarithm problem (DLP) over carefully chosen groups has no efficient solution. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |