|
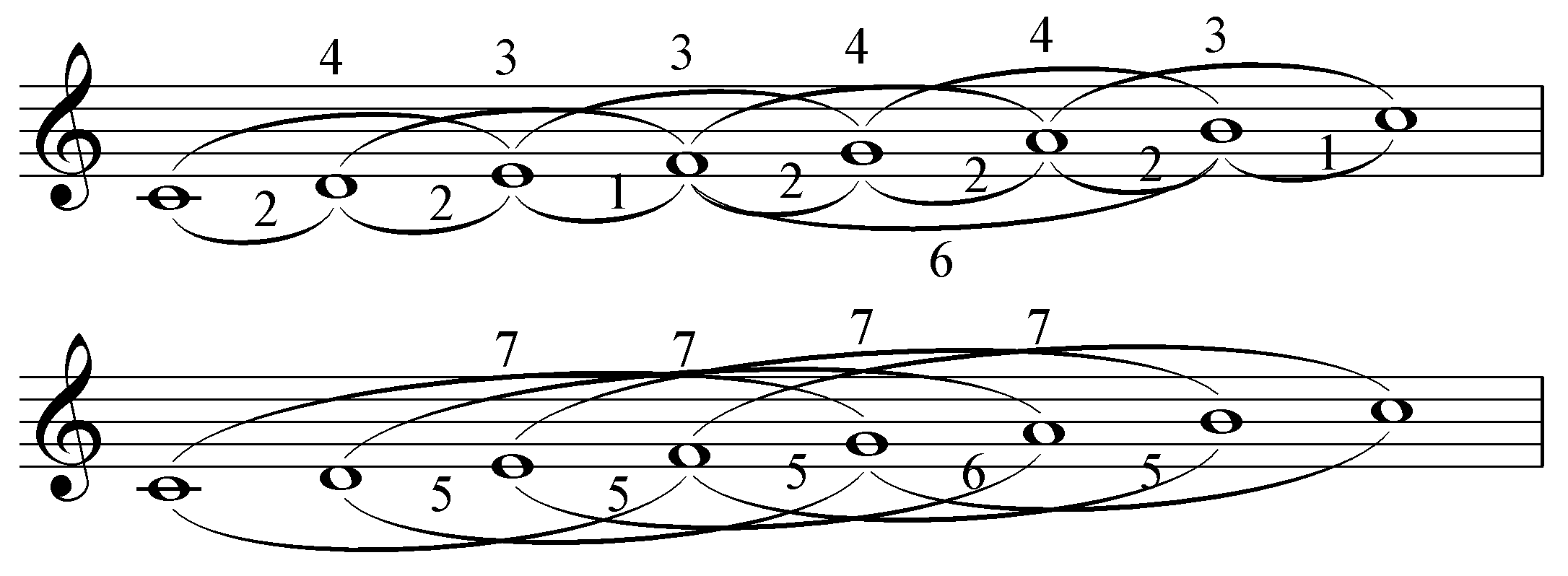
Rothenberg Propriety
In diatonic set theory, Rothenberg propriety is an important concept, lack of contradiction and ambiguity, in the general theory of musical scales which was introduced by David Rothenberg (music theorist), David Rothenberg in a seminal series of papers in 1978. The concept was independently discovered in a more restricted context by Gerald Balzano, who termed it ''coherence''. "Rothenberg calls a scale 'strictly proper' if it possesses a generic ordering, 'proper' if it admits ambiguities but no contradictions, and 'improper' if it admits contradictions." A scale (music), scale is strictly proper if all two step musical interval, intervals are larger than any one step interval, all three step intervals are larger than any two step interval and so on. For instance with the diatonic scale, the one step intervals are the semitone (1) and tone (2), the two step intervals are the minor (3) and major (4) third, the three step intervals are the fourth (5) and tritone (6), the four step ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rothenberg Propriety Diatonic Scale
Rothenberg is a village and a former municipality in the Odenwaldkreis (district) in Hesse, Germany. Since January 2018, it is part of the new town Oberzent. Geography Location Rothenberg lies at elevations between 200 and 500 m in the southern Odenwald in the ''Geo-Naturpark Bergstraße-Odenwald'', 7 km north of Hirschhorn (Neckar), Hirschhorn on the Neckar. The main centre lies in the south of the municipal area as a high settlement in a clearing 430 m high on the ridge of the otherwise wooded Hirschhorner Höhe (heights). The municipal area stretches northwestwards along the Finkenbach. Many tourists visit Billy Rothenberg because of the wonderful natural setting and because of so many possibilities for sports such as swimming, riding bikes, riding horses, hiking, gliding (with a flex-wing or with a glider). Neighbouring communities Rothenberg borders in the north on the town of Beerfelden (Odenwaldkreis), in the east on the town of Eberbach (Baden), Eberbach (R ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Otonal
''Otonality'' and ''utonality'' are terms introduced by Harry Partch to describe chords whose pitch classes are the harmonics or subharmonics of a given fixed tone (identity), respectively. For example: , , ,... or , , ,.... Definition An otonality is a collection of pitches which can be expressed in ratios, expressing their relationship to the fixed tone, that have equal denominators and consecutive numerators. For example, , , and ( just major chord) form an otonality because they can be written as , , . This in turn can be written as an extended ratio 4:5:6. Every otonality is therefore composed of members of a harmonic series. Similarly, the ratios of a utonality share the same numerator and have consecutive denominators. , , , and () form a utonality, sometimes written as , or as . Every utonality is therefore composed of members of a subharmonic series. This term is used extensively by Harry Partch in ''Genesis of a Music''. An otonality corresponds to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Interval Class
In musical set theory, an interval class (often abbreviated: ic), also known as unordered pitch-class interval, interval distance, undirected interval, or "(even completely incorrectly) as 'interval mod 6'" (; ), is the shortest distance in pitch class space between two unordered pitch classes. For example, the interval class between pitch classes 4 and 9 is 5 because 9 − 4 = 5 is less than 4 − 9 = −5 ≡ 7 (mod 12). See modular arithmetic for more on modulo 12. The largest interval class is 6 since any greater interval ''n'' may be reduced to 12 − ''n''. Use of interval classes The concept of interval class accounts for octave, enharmonic, and inversional equivalency. Consider, for instance, the following passage: (To hear a MIDI realization, click the following: In the example above, all four labeled pitch-pairs, or dyads, share a common "intervallic color." In atonal Atonality in i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diminished Fifth
Diminished may refer to: *Diminution In Western culture, Western music and music theory, diminution (from Medieval Latin ''diminutio'', alteration of Latin ''deminutio'', decrease) has four distinct meanings. Diminution may be a form of embellishment (music), embellishment in whic ... in music * "Diminished" (R.E.M. song), from the 1998 album ''Up'' *''Diminished'', a 2024 album by twlv {{disambiguation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Augmented Fourth
Augment or augmentation may refer to: Language *Augment (Indo-European), a syllable added to the beginning of the word in certain Indo-European languages * Augment (Bantu languages), a morpheme that is prefixed to the noun class prefix of nouns in certain Bantu languages *Augment, a name sometimes given to the verbal ''ō-'' prefix in Nahuatl grammar Technology * Augmentation (obstetrics), the process by which the first and/or second stages of an already established labour is accelerated or potentiated by deliberate and artificial means * Augmentation (pharmacology), the combination of two or more drugs to achieve better treatment results *Augmented reality, a live view of a physical, real-world environment whose elements are ''augmented'' by computer-generated sensory input * Augmented cognition, a research field that aims at creating revolutionary human-computer interactions * Augment (Tymshare), a hypertext system derived from Douglas Engelbart's oN-Line System, renamed "Augm ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tritone
In music theory, the tritone is defined as a interval (music), musical interval spanning three adjacent Major second, whole tones (six semitones). For instance, the interval from F up to the B above it (in short, F–B) is a tritone as it can be decomposed into the three adjacent whole tones F–G, G–A, and A–B. Narrowly defined, each of these whole tones must be a step in the scale (music), scale, so by this definition, within a diatonic scale there is only one tritone for each octave. For instance, the above-mentioned interval F–B is the only tritone formed from the notes of the C major scale. More broadly, a tritone is also commonly defined as any interval with a width of three whole tones (spanning six semitones in the chromatic scale), regardless of scale degrees. According to this definition, a diatonic scale contains two tritones for each octave. For instance, the above-mentioned C major scale contains the tritones F–B (from F to the B above it, also called augment ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equal Temperament
An equal temperament is a musical temperament or Musical tuning#Tuning systems, tuning system that approximates Just intonation, just intervals by dividing an octave (or other interval) into steps such that the ratio of the frequency, frequencies of any adjacent pair of notes is the same. This system yields Pitch (music), pitch steps perceived as equal in size, due to the logarithmic changes in pitch frequency. In classical music and Western music in general, the most common tuning system since the 18th century has been 12 equal temperament (also known as ''12 tone equal temperament'', ' or ', informally abbreviated as ''12 equal''), which divides the octave into 12 parts, all of which are equal on a logarithmic scale, with a ratio equal to the twelfth root of two, 12th root of 2, (\sqrt[12] ≈ 1.05946). That resulting smallest interval, the width of an octave, is called a semitone or half step. In Western world, Western countries the term ''equal temperamen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pitch Class
In music, a pitch class (p.c. or pc) is a set of all pitches that are a whole number of octaves apart; for example, the pitch class C consists of the Cs in all octaves. "The pitch class C stands for all possible Cs, in whatever octave position." Important to musical set theory, a pitch class is "all pitches related to each other by octave, enharmonic equivalence, or both." Thus, using scientific pitch notation, the pitch class "C" is the set : = . Although there is no formal upper or lower limit to this sequence, only a few of these pitches are audible to humans. Pitch class is important because human pitch-perception is periodic: pitches belonging to the same pitch class are perceived as having a similar quality or color, a property called " octave equivalence". Psychologists refer to the quality of a pitch as its "chroma". A ''chroma'' is an attribute of pitches (as opposed to ''tone height''), just like hue is an attribute of color. A ''pitch class'' is a set of all p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Octave
In music, an octave (: eighth) or perfect octave (sometimes called the diapason) is an interval between two notes, one having twice the frequency of vibration of the other. The octave relationship is a natural phenomenon that has been referred to as the "basic miracle of music", the use of which is "common in most musical systems". The interval between the first and second harmonics of the harmonic series is an octave. In Western music notation, notes separated by an octave (or multiple octaves) have the same name and are of the same pitch class. To emphasize that it is one of the perfect intervals (including unison, perfect fourth, and perfect fifth), the octave is designated P8. Other interval qualities are also possible, though rare. The octave above or below an indicated note is sometimes abbreviated ''8a'' or ''8va'' (), ''8va bassa'' (, sometimes also ''8vb''), or simply ''8'' for the octave in the direction indicated by placing this mark above or below the staff. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
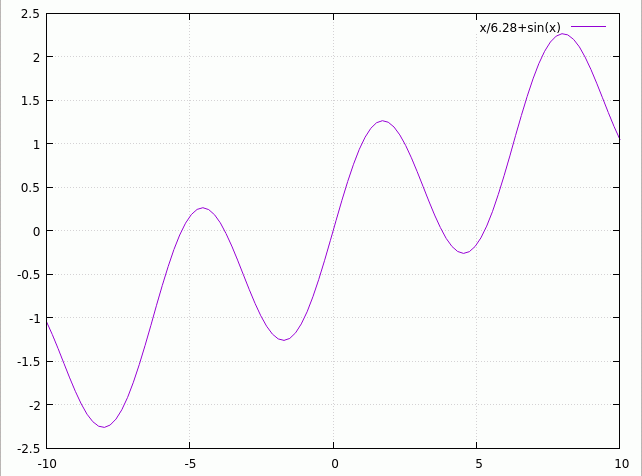
Quasiperiodic Function
In mathematics, a quasiperiodic function is a function that has a certain similarity to a periodic function. A function f is quasiperiodic with quasiperiod \omega if f(z + \omega) = g(z,f(z)), where g is a "''simpler''" function than f. What it means to be "''simpler''" is vague. A simple case (sometimes called arithmetic quasiperiodic) is if the function obeys the equation: :f(z + \omega) = f(z) + C Another case (sometimes called geometric quasiperiodic) is if the function obeys the equation: :f(z + \omega) = C f(z) An example of this is the Jacobi theta function, where :\vartheta(z+\tau;\tau) = e^\vartheta(z;\tau), shows that for fixed \tau it has quasiperiod \tau; it also is periodic with period one. Another example is provided by the Weierstrass sigma function, which is quasiperiodic in two independent quasiperiods, the periods of the corresponding Weierstrass ''℘'' function. Bloch's theorem says that the eigenfunctions of a periodic Schrödinger equation (or o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |