Rothenberg Propriety

In diatonic set theory, Rothenberg propriety is an important concept, lack of contradiction and ambiguity, in the general theory of musical scales which was introduced by David Rothenberg in a seminal series of papers in 1978. The concept was independently discovered in a more restricted context by Gerald Balzano, who termed it ''coherence''.

"Rothenberg calls a scale 'strictly proper' if it possesses a generic ordering, 'proper' if it admits ambiguities but no contradictions, and 'improper' if it admits contradictions." A scale is strictly proper if all two step intervals are larger than any one step interval, all three step intervals are larger than any two step interval and so on. For instance with the diatonic scale, the one step intervals are the semitone (1) and tone (2), the two step intervals are the minor (3) and major (4) third, the three step intervals are the fourth (5) and tritone (6), the four step intervals are the fifth (7) and tritone (6), the five step intervals are the minor (8) and major (9) sixth, and the six step intervals are the minor (t) and major (e) seventh. So it's not strictly proper because the three step intervals and the four step intervals share an interval size (the tritone), causing ambiguity ("two pecificintervals, that sound the same, map onto different codes eneral intervalsMeredith, D. (2011). "Tonal Scales and Minimal Simple Pitch Class Cycles", ''Mathematics and Computation in Music: Third International Conference'', p.174. Springer. ). Such a scale is just called "proper".

For example, the major pentatonic scale is strictly proper:

The pentatonic scales which are proper, but not strictly, are:
* ( Lydian chord)
* (whole tone scale)
* (gamma chord)
* (dominant ninth chord)
* ( dominant minor ninth chord)
The one strictly proper pentatonic scale:
* (major pentatonic)
The heptatonic scales which are proper, but not strictly, are:
* (harmonic minor scale)
* ( diatonic scale)
* (Altered scale)
* ( Major Neapolitan scale)

Propriety may also be considered as scales whose stability = 1, with stability defined as, "the ratio of the number of non-ambiguous undirected intervals...to the total number of undirected intervals," in which case the diatonic scale has a stability of .

The twelve equal scale is strictly proper as is any equal tempered scale because it has only one interval size for each number of steps Most tempered scales are proper too. As another example, the otonal harmonic fragment , , , is strictly proper, with the one step intervals varying in size from to , two step intervals vary from to , three step intervals from to .

Rothenberg hypothesizes that proper scales provide a point or frame of reference which aids perception ("stable gestalt") and that improper scales contradictions require a drone or ostinato to provide a point of reference. (1986).
1/1: The Quarterly Journal of the Just Intonation Network, Volume 2
', p.28. Just Intonation Network.

An example of an improper scale is the Japanese Hirajōshi scale.

Its steps in semitones are 2, 1, 4, 1, 4. The single step intervals vary from the semitone from G to A to the major third from A to C. Two step intervals vary from the minor third from C to E and the tritone, from A to D. There the minor third as a two step interval is smaller than the major third which occurs as a one step interval, creating contradiction ("a contradiction occurs...when the ordering of two specific intervals is the opposite of the ordering of their corresponding generic intervals.").

Mathematical definition of propriety

Rothenberg defined propriety in a very general context; however for nearly all purposes it suffices to consider what in musical contexts is often called a ''periodic scale'', though in fact these correspond to what mathematicians call a quasiperiodic function. These are scales which repeat at a certain fixed interval higher each note in a certain finite set of notes. The fixed interval is typically an octave, and so the scale consists of all notes belonging to a finite number of pitch classes. If ''β''_''i'' denotes a scale element for each integer i, then ''β''_{''i''+''℘''} = ''β''_''i'' + ''Ω'', where ''Ω'' is typically an octave of 1200 cents, though it could be any fixed amount of cents; and ℘ is the number of scale elements in the Ω period, which is sometimes termed the size of the scale.

For any ''i'' one can consider the set of all differences by ''i'' steps between scale elements class(''i'') = . We may in the usual way extend the ordering on the elements of a set to the sets themselves, saying ''A'' < ''B'' if and only if for every ''a'' ∈ ''A'' and ''b'' ∈ ''B'' we have ''a'' < ''b''. Then a scale is ''strictly proper'' if ''i'' < ''j'' implies class(''i'') < class(''j''). It is ''proper'' if ''i'' ≤ ''j'' implies class(''i'') ≤ class(''j''). Strict propriety implies propriety but a proper scale need not be strictly proper; an example is the diatonic scale in equal temperament, where the tritone interval belongs both to the class of the fourth (as an augmented fourth) and to the class of the fifth (as a diminished fifth). Strict propriety is the same as ''coherence'' in the sense of Balzano.

Generic and specific intervals

The interval class class(i) modulo Ω depends only on ''i'' modulo ℘, hence we may also define a version of class, Class(''i''), for pitch classes modulo ''Ω'', which are called generic intervals. The specific pitch classes belonging to Class(i) are then called specific intervals. The class of the unison, Class(0), consists solely of multiples of Ω and is typically excluded from consideration, so that the number of generic intervals is ℘ − 1. Hence the generic intervals are numbered from 1 to ℘ − 1, and a scale is proper if for any two generic intervals ''i'' < ''j'' implies class(''i'') < class(''j''). If we represent the elements of Class(''i'') by intervals reduced to those between the unison and Ω, we may order them as usual, and so define propriety by stating that ''i'' < ''j'' for generic classes entails Class(''i'') < Class(''j''). This procedure, while a good deal more convoluted than the definition as originally stated, is how the matter is normally approached in diatonic set theory.

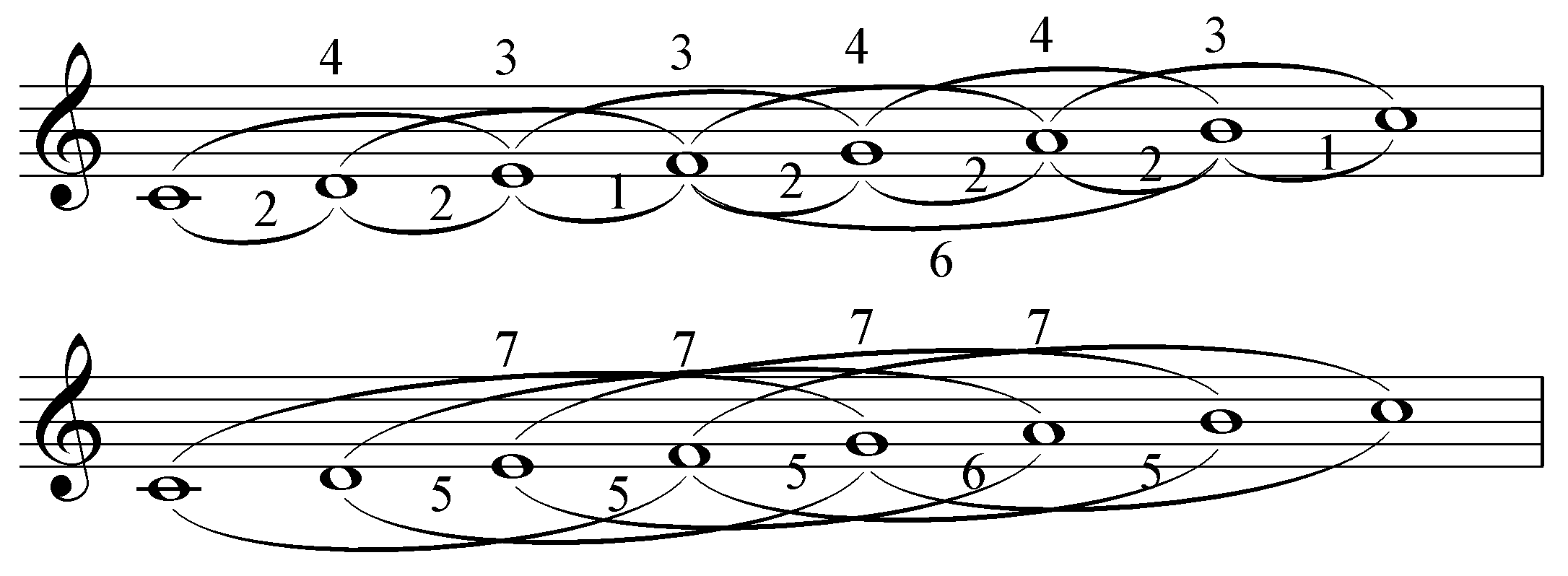
Consider the diatonic (major) scale in the common 12 tone equal temperament, which follows the pattern (in semitones) 2-2-1-2-2-2-1. No interval in this scale, spanning any given number of scale steps, is narrower (consisting of fewer semitones) than an interval spanning fewer scale steps. For example, one cannot find a fourth in this scale that is smaller than a third: the smallest fourths are five semitones wide, and the largest thirds are four semitones. Therefore, the diatonic scale is proper. However, there is an interval that contains the same number of semitones as an interval spanning fewer scale degrees: the augmented fourth (F G A B) and the diminished fifth (B C D E F) are both six semitones wide. Therefore, the diatonic scale is proper but not strictly proper.

On the other hand, consider the enigmatic scale, which follows the pattern 1-3-2-2-2-1-1. It is possible to find intervals in this scale that are narrower than other intervals in the scale spanning fewer scale steps: for example, the fourth built on the 6th scale step is three semitones wide, while the third built on the 2nd scale step is five semitones wide. Therefore, the enigmatic scale is not proper.

Diatonic scale theory

Balzano introduced the idea of attempting to characterize the diatonic scale in terms of propriety. There are no strictly proper seven-note scales in 12 equal temperament; however, there ''are'' five proper scales, one of which is the diatonic scale. Here transposition and modes are not counted separately, so that ''diatonic scale'' encompasses both the major diatonic scale and the natural minor scale beginning with any pitch. Each of these scales, if spelled correctly, has a version in any meantone tuning, and when the fifth is flatter than 700 cents, they all become strictly proper. In particular, five of the seven strictly proper seven-note scales in 19 equal temperament are one of these scales. The five scales are:
* Diatonic: C D E F G A B
* Melodic/ascending minor/jazz minor: C D E F G A B
* Harmonic minor: C D E F G A B
* Harmonic major: C D E F G A B
* Major Locrian: C D E F G A B

In any meantone system with fifths flatter than 700 cents, one also has the following strictly proper scale: C D E F G A B (which is Phrygian Dominant 4 scale).

The diatonic, ascending minor, harmonic minor, harmonic major and this last unnamed scale all contain complete circles of three major and four minor thirds, variously arranged. The Locrian major scale has a circle of four major and two minor thirds, along with a diminished third, which in septimal meantone temperament approximates a septimal major second of ratio . The other scales are all of the scales with a complete circle of three major and four minor thirds, which since ()³ ()⁴ = , tempered to two octaves in meantone, is indicative of meantone.

The first three scales are of basic importance to common practice music, and the harmonic major scale often used, and that the diatonic scale is not singled out by propriety is perhaps less interesting than that the backbone scales of diatonic practice all are.

See also

*Deep scale property

References

Further reading

* Gerald J. Balzano, ''The Group-Theoretic Description of 12-fold and Microtonal Pitch Systems'', Computer Music Journal 4/4 (1980) 66–84
* Gerald J. Balzano, ''The Pitch Set as a Level of Description for Studying Musical Pitch Perception'', in Music, Mind, and Brain, Manfred Clynes, ed., Plenum Press, 1982
* David Rothenberg, ''A Model for Pattern Perception with Musical Applications Part I: Pitch Structures as order-preserving maps'', Mathematical Systems Theory 11 (1978) 199–23


{{Set theory (music)

Musical set theory
Music psychology