|
Rhomb Spar
In plane Euclidean geometry, a rhombus (: rhombi or rhombuses) is a quadrilateral whose four sides all have the same length. Another name is equilateral quadrilateral, since equilateral means that all of its sides are equal in length. The rhombus is often called a "diamond", after the diamonds suit in playing card A playing card is a piece of specially prepared card stock, heavy paper, thin cardboard, plastic-coated paper, cotton-paper blend, or thin plastic that is marked with distinguishing motifs. Often the front (face) and back of each card has a f ...s which resembles the projection of an Octahedron#Orthogonal projections, octahedral diamond, or a lozenge (shape), lozenge, though the former sometimes refers specifically to a rhombus with a 60° angle (which some authors call a calisson after calisson, the French sweet—also see Polyiamond), and the latter sometimes refers specifically to a rhombus with a 45° angle. Every rhombus is simple polygon, simple (non-self ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quadrilateral
In Euclidean geometry, geometry a quadrilateral is a four-sided polygon, having four Edge (geometry), edges (sides) and four Vertex (geometry), corners (vertices). The word is derived from the Latin words ''quadri'', a variant of four, and ''latus'', meaning "side". It is also called a tetragon, derived from Greek "tetra" meaning "four" and "gon" meaning "corner" or "angle", in analogy to other polygons (e.g. pentagon). Since "gon" means "angle", it is analogously called a quadrangle, or 4-angle. A quadrilateral with vertices A, B, C and D is sometimes denoted as \square ABCD. Quadrilaterals are either simple polygon, simple (not self-intersecting), or complex polygon, complex (self-intersecting, or crossed). Simple quadrilaterals are either convex polygon, convex or concave polygon, concave. The Internal and external angle, interior angles of a simple (and Plane (geometry), planar) quadrilateral ''ABCD'' add up to 360 Degree (angle), degrees, that is :\angle A+\angle B+\angle ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polyiamond
A polyiamond (also polyamond or simply iamond, or sometimes triangular polyomino) is a polyform whose base form is an equilateral triangle. The word ''polyiamond'' is a back-formation from ''diamond'', because this word is often used to describe the shape of a pair of equilateral triangles placed base to base, and the initial 'di-' looks like a Greek prefix meaning 'two-' (though ''diamond'' actually derives from Greek '' ἀδάμας'' - also the basis for the word "adamant"). The name was suggested by recreational mathematics writer Thomas H. O'Beirne in ''New Scientist'' 1961 number 1, page 164. Counting The basic combinatorial question is, How many different polyiamonds exist with a given number of cells? Like polyominoes, polyiamonds may be either free or one-sided. Free polyiamonds are invariant under reflection as well as translation and rotation. One-sided polyiamonds distinguish reflections. The number of free ''n''-iamonds for ''n'' = 1, 2, 3, ... is: :1, 1, 1, 3 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Deirdre Smeltzer
Deirdre Longacher Smeltzer (born 1964) is an American mathematician, mathematics educator, textbook author, and academic administrator. A former professor, dean, and vice president at Eastern Mennonite University, she is Senior Director for Programs at the Mathematical Association of America. Education and career Smeltzer was a mathematics major at Eastern Mennonite University, graduating in 1987 with a minor in Bible study. At Eastern Mennonite, mathematicians Millard Showalter and Del Snyder became faculty mentors, encouraging her to continue in advanced mathematics. She went on to graduate study in mathematics at the University of Virginia, earning a master's degree and completing her Ph.D. in 1994, with the dissertation ''Topics in Difference Sets in 2-Groups'' on difference sets in group theory, supervised by Harold Ward. She became a faculty member at the University of St. Thomas, a Catholic university in Saint Paul, Minnesota, before returning to Eastern Mennonite Univ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
If And Only If
In logic and related fields such as mathematics and philosophy, "if and only if" (often shortened as "iff") is paraphrased by the biconditional, a logical connective between statements. The biconditional is true in two cases, where either both statements are true or both are false. The connective is biconditional (a statement of material equivalence), and can be likened to the standard material conditional ("only if", equal to "if ... then") combined with its reverse ("if"); hence the name. The result is that the truth of either one of the connected statements requires the truth of the other (i.e. either both statements are true, or both are false), though it is controversial whether the connective thus defined is properly rendered by the English "if and only if"—with its pre-existing meaning. For example, ''P if and only if Q'' means that ''P'' is true whenever ''Q'' is true, and the only case in which ''P'' is true is if ''Q'' is also true, whereas in the case of ''P if Q ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Self-intersecting Polygons
Self-intersecting polygons, crossed polygons, or self-crossing polygons are polygons some of whose edges cross each other. They contrast with simple polygons, whose edges never cross. Some types of self-intersecting polygons are: *the crossed quadrilateral, with four edges **the antiparallelogram, a crossed quadrilateral with alternate edges of equal length ***the crossed rectangle, an antiparallelogram whose edges are two opposite sides and the two diagonals of a rectangle, hence having two edges parallel * Star polygons ** pentagram, with five edges ** hexagram, with six edges ** heptagram, with seven edges ** octagram, with eight edges ** enneagram or nonagram, with nine edges ** decagram, with ten edges ** hendecagram, with eleven edges **dodecagram, with twelve edges ** icositetragram, with twenty four edges ** 257-gram, with two hundred and fifty seven edges See also * *Complex polygon The term ''complex polygon'' can mean two different things: * In geometry, a polyg ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Haltern Am See, Naturpark Hohe Mark, Hohemarkenbusch, Baumstamm -- 2024 -- 4411 (kreativ 2)
Haltern am See (''Haltern at the lake'', before December 2001 only Haltern) is a medium-sized town in the northern part of the district of Recklinghausen in the ''Regierungsbezirk'' Münster in North Rhine-Westphalia. The town is located in the northern Ruhr area, directly bordering the Münsterland region. In terms of natural geography, it belongs to the Westmünsterland. The town is about north of Düsseldorf. Haltern is surrounded by the and forest areas and is sparsely industrialized. The and the Haard, Borkenberge, and Hohe Mark forest areas are popular local recreation areas. Geography and Nature Haltern am See is a picturesque city in western Germany with an abundance of natural beauty in its surroundings. The city is situated on the shores of the Halterner Stausee, which is a popular destination for swimming, boating, and hiking. The area around the lake is characterized by lush green forests, rolling hills, and sprawling meadows. The town is surrounded by several ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cross Section (geometry)
In geometry and science, a cross section is the non-empty intersection (set theory), intersection of a solid body in three-dimensional space with a Plane (geometry), plane, or the analog in higher-dimensional spaces. Cutting an object into slices creates many parallel cross-sections. The boundary of a cross-section in three-dimensional space that is parallel to two of the Cartesian coordinate system, axes, that is, parallel to the plane determined by these axes, is sometimes referred to as a contour line; for example, if a plane cuts through mountains of a raised-relief map parallel to the ground, the result is a contour line in two-dimensional space showing points on the surface of the mountains of equal elevation. In technical drawing a cross-section, being a Planar projection, projection of an object onto a plane that intersects it, is a common tool used to depict the internal arrangement of a 3-dimensional object in two dimensions. It is traditionally crosshatched with th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
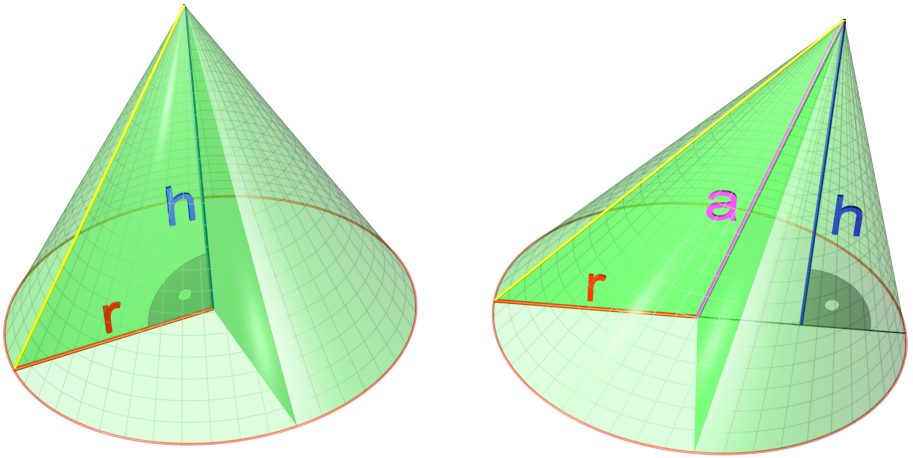
Cone
In geometry, a cone is a three-dimensional figure that tapers smoothly from a flat base (typically a circle) to a point not contained in the base, called the '' apex'' or '' vertex''. A cone is formed by a set of line segments, half-lines, or lines connecting a common point, the apex, to all of the points on a base. In the case of line segments, the cone does not extend beyond the base, while in the case of half-lines, it extends infinitely far. In the case of lines, the cone extends infinitely far in both directions from the apex, in which case it is sometimes called a ''double cone''. Each of the two halves of a double cone split at the apex is called a ''nappe''. Depending on the author, the base may be restricted to a circle, any one-dimensional quadratic form in the plane, any closed one-dimensional figure, or any of the above plus all the enclosed points. If the enclosed points are included in the base, the cone is a solid object; otherwise it is an open surface ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bicone
In geometry, a bicone or dicone (from , and Greek: ''di-'', both meaning "two") is the three-dimensional surface of revolution of a rhombus around one of its axes of symmetry. Equivalently, a bicone is the surface created by joining two congruent right circular cones at their bases. A bicone has circular symmetry and orthogonal bilateral symmetry. Geometry For a bicone with radius r and half-height h, the volume is :V = \frac \pi r^2 h and the surface area is :A =2\pi r \ell\, where :\ell = \sqrt is the slant height. See also * Sphericon In solid geometry, the sphericon is a solid that has a continuous developable surface with two Congruence (geometry), congruent, semicircle, semi-circular edges, and four Vertex (geometry), vertices that define a square. It is a member of a spe ... * Biconical antenna References External links * Elementary geometry Surfaces {{Elementary-geometry-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Archimedes
Archimedes of Syracuse ( ; ) was an Ancient Greece, Ancient Greek Greek mathematics, mathematician, physicist, engineer, astronomer, and Invention, inventor from the ancient city of Syracuse, Sicily, Syracuse in History of Greek and Hellenistic Sicily, Sicily. Although few details of his life are known, based on his surviving work, he is considered one of the leading scientists in classical antiquity, and one of the greatest mathematicians of all time. Archimedes anticipated modern calculus and mathematical analysis, analysis by applying the concept of the Cavalieri's principle, infinitesimals and the method of exhaustion to derive and rigorously prove many geometry, geometrical theorem, theorems, including the area of a circle, the surface area and volume of a sphere, the area of an ellipse, the area under a parabola, the volume of a segment of a paraboloid of revolution, the volume of a segment of a hyperboloid of revolution, and the area of a spiral. Archimedes' other math ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
For The Learning Of Mathematics
''For the Learning of Mathematics'' is a triannual peer-reviewed academic journal covering mathematics education. It was established in 1981 by David Wheeler. Abstracting and indexing The journal is abstracted and indexed in: * EBSCO databases *Education Resources Information Center *Index Islamicus * ProQuest databases *Scopus Reception In 2012, a survey of researchers in the field ranked the journal with an A (the second highest ranking, below A*). In 2017, another ranking of journals placed it in the top tier. At the same time, the high ranking in both of these reviews was questioned, suggesting that the journal more properly belongs in the mid-tier. Editors-in-chief The following persons are or have been editor-in-chief An editor-in-chief (EIC), also known as lead editor or chief editor, is a publication's editorial leader who has final responsibility for its operations and policies. The editor-in-chief heads all departments of the organization and is held accoun ...: *David ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclid
Euclid (; ; BC) was an ancient Greek mathematician active as a geometer and logician. Considered the "father of geometry", he is chiefly known for the '' Elements'' treatise, which established the foundations of geometry that largely dominated the field until the early 19th century. His system, now referred to as Euclidean geometry, involved innovations in combination with a synthesis of theories from earlier Greek mathematicians, including Eudoxus of Cnidus, Hippocrates of Chios, Thales and Theaetetus. With Archimedes and Apollonius of Perga, Euclid is generally considered among the greatest mathematicians of antiquity, and one of the most influential in the history of mathematics. Very little is known of Euclid's life, and most information comes from the scholars Proclus and Pappus of Alexandria many centuries later. Medieval Islamic mathematicians invented a fanciful biography, and medieval Byzantine and early Renaissance scholars mistook him for the earlier philo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |