|
Rendleman–Bartter Model
The Rendleman–Bartter model (Richard J. Rendleman, Jr. and Brit J. Bartter) in finance is a short-rate model describing the evolution of interest rates. It is a "one factor model" as it describes interest rate movements as driven by only one source of market risk. It can be used in the valuation of interest rate derivatives. It is a stochastic asset model. The model specifies that the instantaneous interest rate follows a geometric Brownian motion: :dr_t = \theta r_t\,dt + \sigma r_t\,dW_t where ''Wt'' is a Wiener process modelling the random market risk factor. The drift parameter, \theta, represents a constant expected instantaneous rate of change in the interest rate, while the standard deviation parameter, \sigma, determines the volatility of the interest rate. This is one of the early models of the short-term interest rates, using the same stochastic process as the one already used to describe the dynamics of the underlying price in stock options. Its main disadvantage i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Finance
Mathematical finance, also known as quantitative finance and financial mathematics, is a field of applied mathematics, concerned with mathematical modeling in the financial field. In general, there exist two separate branches of finance that require advanced quantitative techniques: derivatives pricing on the one hand, and risk and portfolio management on the other. Mathematical finance overlaps heavily with the fields of computational finance and financial engineering. The latter focuses on applications and modeling, often with the help of stochastic asset models, while the former focuses, in addition to analysis, on building tools of implementation for the models. Also related is quantitative investing, which relies on statistical and numerical models (and lately machine learning) as opposed to traditional fundamental analysis when managing portfolios. French mathematician Louis Bachelier's doctoral thesis, defended in 1900, is considered the first scholarly work on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stochastic Process
In probability theory and related fields, a stochastic () or random process is a mathematical object usually defined as a family of random variables in a probability space, where the index of the family often has the interpretation of time. Stochastic processes are widely used as mathematical models of systems and phenomena that appear to vary in a random manner. Examples include the growth of a bacterial population, an electrical current fluctuating due to thermal noise, or the movement of a gas molecule. Stochastic processes have applications in many disciplines such as biology, chemistry, ecology Ecology () is the natural science of the relationships among living organisms and their Natural environment, environment. Ecology considers organisms at the individual, population, community (ecology), community, ecosystem, and biosphere lev ..., neuroscience, physics, image processing, signal processing, stochastic control, control theory, information theory, computer scien ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Interest Rates
An interest rate is the amount of interest due per period, as a proportion of the amount lent, deposited, or borrowed (called the principal sum). The total interest on an amount lent or borrowed depends on the principal sum, the interest rate, the compounding frequency, and the length of time over which it is lent, deposited, or borrowed. The annual interest rate is the rate over a period of one year. Other interest rates apply over different periods, such as a month or a day, but they are usually annualized. The interest rate has been characterized as "an index of the preference . . . for a dollar of present ncomeover a dollar of future income". The borrower wants, or needs, to have money sooner, and is willing to pay a fee—the interest rate—for that privilege. Influencing factors Interest rates vary according to: * the government's directives to the central bank to accomplish the government's goals * the currency of the principal sum lent or borrowed * the term to mat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prentice Hall
Prentice Hall was a major American publishing#Textbook_publishing, educational publisher. It published print and digital content for the 6–12 and higher-education market. It was an independent company throughout the bulk of the twentieth century. In its last few years it was owned by, then absorbed into, Savvas Learning Company. In the Web era, it distributed its technical titles through the Safari Books Online e-reference service for some years. History On October 13, 1913, law professor Charles Gerstenberg and his student Richard Ettinger founded Prentice Hall. Gerstenberg and Ettinger took their mothers' maiden names, Prentice and Hall, to name their new company. At the time the name was usually styled as Prentice-Hall (as seen for example on many title pages), per an orthographic norm for Dash#Relationships and connections, coordinate elements within such compounds (compare also ''McGraw-Hill'' with later styling as ''McGraw Hill''). Prentice-Hall became known as a publi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Underlying
In finance, a derivative is a contract between a buyer and a seller. The derivative can take various forms, depending on the transaction, but every derivative has the following four elements: # an item (the "underlier") that can or must be bought or sold, # a future act which must occur (such as a sale or purchase of the underlier), # a price at which the future transaction must take place, and # a future date by which the act (such as a purchase or sale) must take place. A derivative's value depends on the performance of the underlier, which can be a commodity (for example, corn or oil), a financial instrument (e.g. a stock or a bond), a price index, a currency, or an interest rate. Derivatives can be used to insure against price movements ( hedging), increase exposure to price movements for speculation, or get access to otherwise hard-to-trade assets or markets. Most derivatives are price guarantees. But some are based on an event or performance of an act rather than a pri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Binomial Options Pricing Model
In finance, the binomial options pricing model (BOPM) provides a generalizable numerical method for the valuation of options. Essentially, the model uses a "discrete-time" ( lattice based) model of the varying price over time of the underlying financial instrument, addressing cases where the closed-form Black–Scholes formula is wanting, which in general does not exist for the BOPM. The binomial model was first proposed by William Sharpe in the 1978 edition of ''Investments'' (), and formalized by Cox, Ross and Rubinstein in 1979 and by Rendleman and Bartter in that same year. For binomial trees as applied to fixed income and interest rate derivatives see . Use of the model The Binomial options pricing model approach has been widely used since it is able to handle a variety of conditions for which other models cannot easily be applied. This is largely because the BOPM is based on the description of an underlying instrument over a period of time rather than a single point ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mean Reversion (finance)
Mean reversion is a financial term for the assumption that an asset's price will tend to converge to the average price over time. Using mean reversion as a timing strategy involves both the identification of the trading range for a security and the computation of the average price using quantitative methods. Mean reversion is a phenomenon that can be exhibited in a host of financial time-series data, from price data, earnings data, and book value. When the current market price is less than the average past price, the security is considered attractive for purchase, with the expectation that the price will rise. When the current market price is above the average past price, the market price is expected to fall. In other words, deviations from the average price are expected to revert to the average. This expectation serves as the cornerstone of multiple trading strategies. Stock reporting services commonly offer moving averages for periods such as 50 and 100 days. While reporting s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stock Options
In finance, an option is a contract which conveys to its owner, the ''holder'', the right, but not the obligation, to buy or sell a specific quantity of an underlying asset or instrument at a specified strike price on or before a specified date, depending on the style of the option. Options are typically acquired by purchase, as a form of compensation, or as part of a complex financial transaction. Thus, they are also a form of asset (or contingent liability) and have a valuation that may depend on a complex relationship between underlying asset price, time until expiration, market volatility, the risk-free rate of interest, and the strike price of the option. Options may be traded between private parties in ''over-the-counter'' (OTC) transactions, or they may be exchange-traded in live, public markets in the form of standardized contracts. Definition and application An option is a contract that allows the holder the right to buy or sell an underlying asset or financial i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
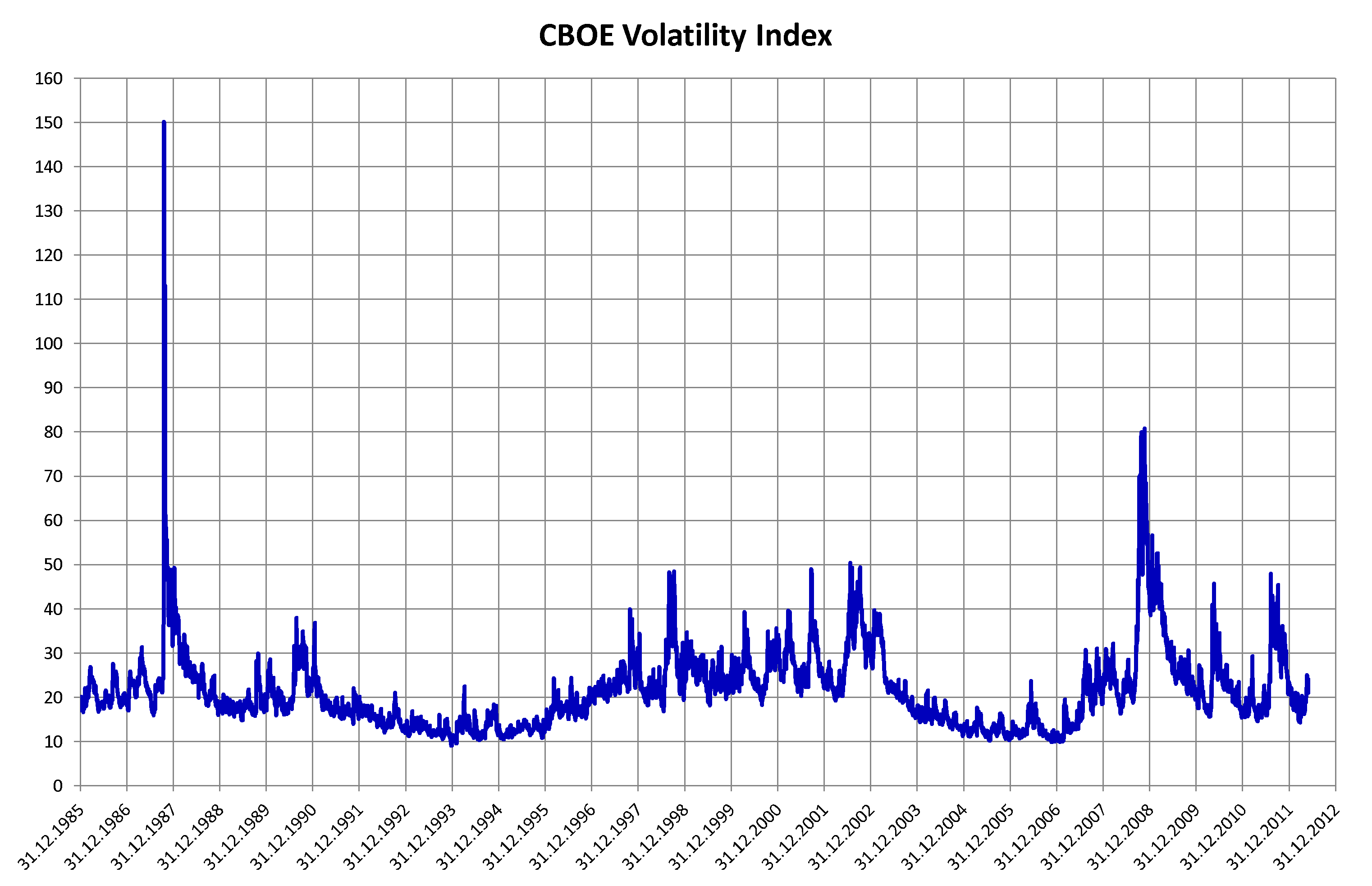
Volatility (finance)
In finance, volatility (usually denoted by "sigma, σ") is the Variability (statistics), degree of variation of a trading price series over time, usually measured by the standard deviation of logarithmic returns. Historic volatility measures a time series of past market prices. Implied volatility looks forward in time, being derived from the market price of a market-traded derivative (in particular, an option). Volatility terminology Volatility as described here refers to the actual volatility, more specifically: * actual current volatility of a financial instrument for a specified period (for example 30 days or 90 days), based on historical prices over the specified period with the last observation the most recent price. * actual historical volatility which refers to the volatility of a financial instrument over a specified period but with the last observation on a date in the past **near synonymous is realized volatility, the square root of the realized variance, in turn c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Short-rate Model
A short-rate model, in the context of interest rate derivatives, is a mathematical model that describes the future evolution of interest rates by describing the future evolution of the short rate, usually written r_t \,. The short rate Under a short rate model, the stochastic state variable is taken to be the instantaneous spot rate. The short rate, r_t \,, then, is the (Compound interest#Continuous compounding, continuously compounded, annualized) interest rate at which an entity can borrow money for an infinitesimally short period of time from time t. Specifying the current short rate does not specify the entire yield curve. However, arbitrage, no-arbitrage arguments show that, under some fairly relaxed technical conditions, if we model the evolution of r_t \, as a stochastic process under a risk-neutral measure Q, then the price at time t of a zero-coupon bond maturing at time T with a payoff of 1 is given by : P(t,T) = \operatorname^Q\left[\left. \exp \ \mathcal_t \right], w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Standard Deviation
In statistics, the standard deviation is a measure of the amount of variation of the values of a variable about its Expected value, mean. A low standard Deviation (statistics), deviation indicates that the values tend to be close to the mean (also called the expected value) of the set, while a high standard deviation indicates that the values are spread out over a wider range. The standard deviation is commonly used in the determination of what constitutes an outlier and what does not. Standard deviation may be abbreviated SD or std dev, and is most commonly represented in mathematical texts and equations by the lowercase Greek alphabet, Greek letter Sigma, σ (sigma), for the population standard deviation, or the Latin script, Latin letter ''s'', for the sample standard deviation. The standard deviation of a random variable, Sample (statistics), sample, statistical population, data set, or probability distribution is the square root of its variance. (For a finite population, v ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wiener Process
In mathematics, the Wiener process (or Brownian motion, due to its historical connection with Brownian motion, the physical process of the same name) is a real-valued continuous-time stochastic process discovered by Norbert Wiener. It is one of the best known Lévy processes (càdlàg stochastic processes with stationary increments, stationary independent increments). It occurs frequently in pure and applied mathematics, economy, economics, quantitative finance, evolutionary biology, and physics. The Wiener process plays an important role in both pure and applied mathematics. In pure mathematics, the Wiener process gave rise to the study of continuous time martingale (probability theory), martingales. It is a key process in terms of which more complicated stochastic processes can be described. As such, it plays a vital role in stochastic calculus, diffusion processes and even potential theory. It is the driving process of Schramm–Loewner evolution. In applied mathematics, the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |