 |
Random Generalized Lotka–Volterra Model
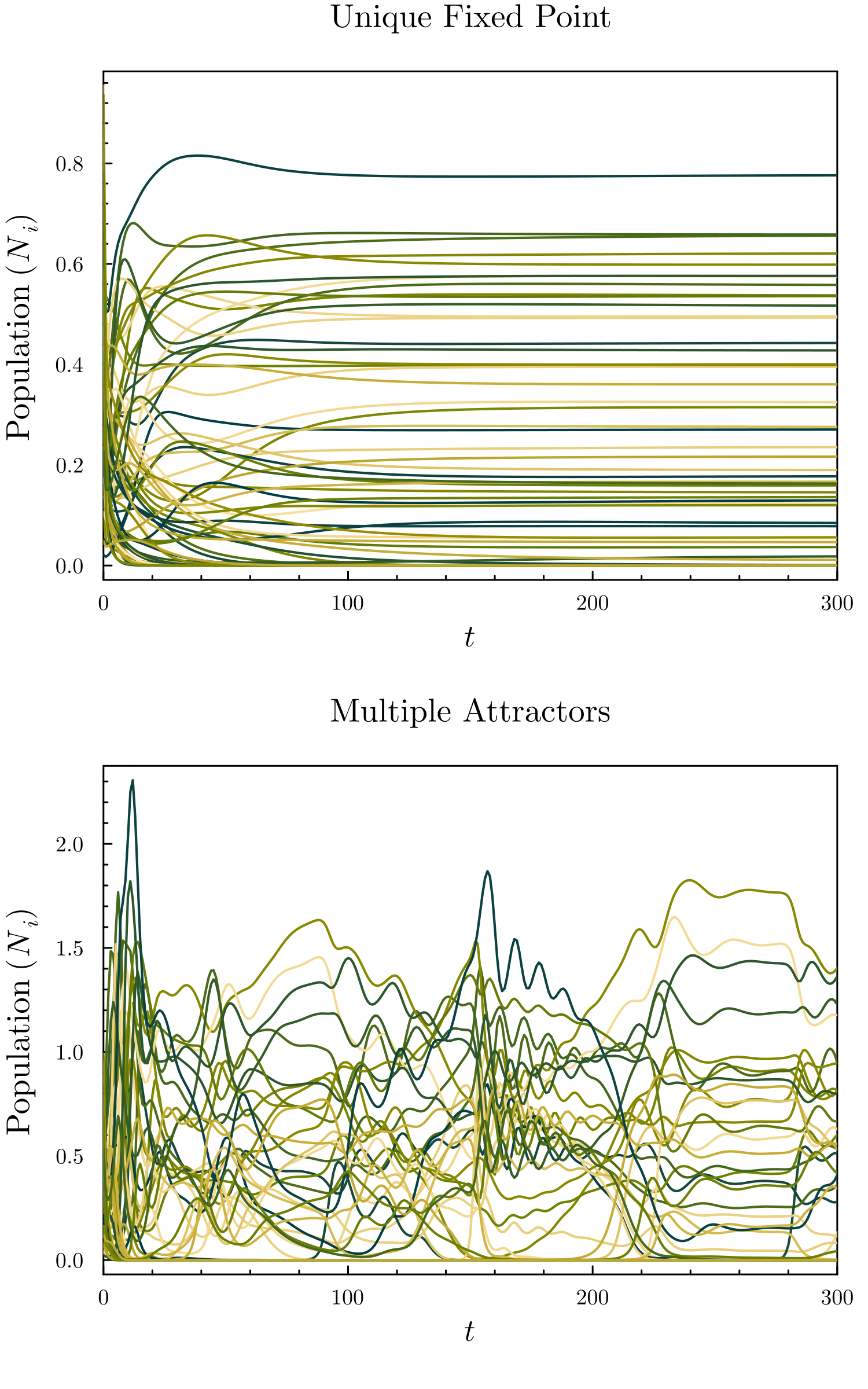
The random generalized Lotka–Volterra model (rGLV) is an ecological model and Random dynamical system, random set of coupled ordinary differential equations where the parameters of the generalized Lotka–Volterra equation are sampled from a probability distribution, analogously to quenched disorder. The rGLV models dynamics of a community of species in which each species' abundance grows towards a carrying capacity but is depleted due to Competition (biology), competition from the presence of other species. It is often analyzed in the Thermodynamic limit, many-species limit using tools from statistical physics, in particular from spin glass theory. The rGLV has been used as a tool to analyze Emergence, emergent macroscopic behavior in microbial communities with dense, strong interspecies interactions. The model has served as a context for theoretical investigations studying Diversity (ecology), diversity-Stability (ecology), stability relations in community ecology and proper ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Random Matrix
In probability theory and mathematical physics, a random matrix is a matrix-valued random variable—that is, a matrix in which some or all of its entries are sampled randomly from a probability distribution. Random matrix theory (RMT) is the study of properties of random matrices, often as they become large. RMT provides techniques like mean-field theory, diagrammatic methods, the cavity method, or the replica method to compute quantities like traces, spectral densities, or scalar products between eigenvectors. Many physical phenomena, such as the spectrum of nuclei of heavy atoms, the thermal conductivity of a lattice, or the emergence of quantum chaos, can be modeled mathematically as problems concerning large, random matrices. Applications Physics In nuclear physics, random matrices were introduced by Eugene Wigner to model the nuclei of heavy atoms. Wigner postulated that the spacings between the lines in the spectrum of a heavy atom nucleus should resemble the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Invasibility
Alien species, or species that are not native, invade habitats and alter ecosystems around the world. Invasive species are only considered invasive if they are able to survive and sustain themselves in their new environment. A habitat and the environment around it has natural flaws that make them vulnerable to invasive species. The level of vulnerability of a habitat to invasions from outside species is defined as its invasibility. One must be careful not to get this confused with invasiveness, which relates to the species itself and its ability to invade an ecosystem.Alpert, P., Bone, E., & Holzapfel, C. (2000). Invasiveness, invasibility and the role of environmental stress in the spread of non-native plants. ''Perspectives in Plant Ecology, Evolution and Systematics,'' ''3''(1), 52-66. doi:10.1078/1433-8319-00004 There are many factors, abiotic and biotic, that can raise or lower a habitat's invasibility, such as stress, disturbance, nutrient levels, climate, and pre-existin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Standard Normal Random Variable
In probability theory and statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is f(x) = \frac e^\,. The parameter is the mean or expectation of the distribution (and also its median and mode), while the parameter \sigma^2 is the variance. The standard deviation of the distribution is (sigma). A random variable with a Gaussian distribution is said to be normally distributed, and is called a normal deviate. Normal distributions are important in statistics and are often used in the natural and social sciences to represent real-valued random variables whose distributions are not known. Their importance is partly due to the central limit theorem. It states that, under some conditions, the average of many samples (observations) of a random variable with finite mean and variance is itself a random variable—whose distribution converge ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Mean-field Theory
In physics and probability theory, Mean-field theory (MFT) or Self-consistent field theory studies the behavior of high-dimensional random (stochastic) models by studying a simpler model that approximates the original by averaging over Degrees of freedom (statistics), degrees of freedom (the number of values in the final calculation of a statistic that are free to vary). Such models consider many individual components that interact with each other. The main idea of MFT is to replace all fundamental interaction, interactions to any one body with an average or effective interaction, sometimes called a ''molecular field''. This reduces any many-body problem into an effective one-body problem. The ease of solving MFT problems means that some insight into the behavior of the system can be obtained at a lower computational cost. MFT has since been applied to a wide range of fields outside of physics, including statistical inference, graphical models, neuroscience, artificial intelligenc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Self-averaging
A self-averaging physical property of a disordered system is one that can be described by averaging over a sufficiently large sample. The concept was introduced by Ilya Mikhailovich Lifshitz. Definition Frequently in physics one comes across situations where quenched randomness plays an important role. Any physical property ''X'' of such a system, would require an averaging over all disorder realisations. The system can be completely described by the average 'X''where ..denotes averaging over realisations (“averaging over samples”) provided the relative variance ''R''''X'' = ''V''''X'' / 'X''sup>2 → 0 as ''N''→∞, where ''V''''X'' = 'X''2nbsp;− 'X''sup>2 and ''N'' denotes the size of the realisation. In such a scenario a single large system is sufficient to represent the whole ensemble. Such quantities are called self-averaging. Away from criticality, when the larger lattice is built from smaller blocks, then ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Cavity Method
The cavity method is a mathematical method presented by Marc Mézard, Giorgio Parisi and Miguel Angel Virasoro in 1987 to derive and solve some mean field-type models in statistical physics, specially adapted to disordered systems. The method has been used to compute properties of ground states in many condensed matter and optimization problems. Initially invented to deal with the Sherrington–Kirkpatrick model of spin glasses, the cavity method has shown wider applicability. It can be regarded as a generalization of the Bethe– Peierls iterative method in tree-like graphs, to the case of a graph with loops that are not too short. The cavity method can solve many problems also solvable using the replica trick but has the advantage of being more intuitive and less mathematically subtle than replica-based methods. The cavity method proceeds by perturbing a large system with the addition of a non-thermodynamic number of additional constituents and approximating the response of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Thermodynamic Limit
In statistical mechanics, the thermodynamic limit or macroscopic limit, of a system is the Limit (mathematics), limit for a large number of particles (e.g., atoms or molecules) where the volume is taken to grow in proportion with the number of particles.S.J. Blundell and K.M. Blundell, "Concepts in Thermal Physics", Oxford University Press (2009) The thermodynamic limit is defined as the limit of a system with a large volume, with the particle density held fixed: : N \to \infty,\, V \to \infty,\, \frac N V =\text In this limit, macroscopic thermodynamics is valid. There, thermal fluctuations in global quantities are negligible, and all List of thermodynamic properties, thermodynamic quantities, such as pressure and energy, are simply functions of the thermodynamic variables, such as temperature and density. For example, for a large volume of gas, the fluctuations of the total internal energy are negligible and can be ignored, and the average internal energy can be predicted fro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Chaos Theory
Chaos theory is an interdisciplinary area of Scientific method, scientific study and branch of mathematics. It focuses on underlying patterns and Deterministic system, deterministic Scientific law, laws of dynamical systems that are highly sensitive to initial conditions. These were once thought to have completely random states of disorder and irregularities. Chaos theory states that within the apparent randomness of chaotic complex systems, there are underlying patterns, interconnection, constant feedback loops, repetition, self-similarity, fractals and self-organization. The butterfly effect, an underlying principle of chaos, describes how a small change in one state of a deterministic nonlinear system can result in large differences in a later state (meaning there is sensitive dependence on initial conditions). A metaphor for this behavior is that a butterfly flapping its wings in Brazil can cause or prevent a tornado in Texas. Text was copied from this source, which is avai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Steady State
In systems theory, a system or a process is in a steady state if the variables (called state variables) which define the behavior of the system or the process are unchanging in time. In continuous time, this means that for those properties ''p'' of the system, the partial derivative with respect to time is zero and remains so: : \frac = 0 \quad \text t. In discrete time, it means that the first difference of each property is zero and remains so: : p_t-p_=0 \quad \text t. The concept of a steady state has relevance in many fields, in particular thermodynamics, economics, and engineering. If a system is in a steady state, then the recently observed behavior of the system will continue into the future. In stochastic systems, the probabilities that various states will be repeated will remain constant. For example, see ' for the derivation of the steady state. In many systems, a steady state is not achieved until some time after the system is started or initiated. This initial sit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Phase Transition
In physics, chemistry, and other related fields like biology, a phase transition (or phase change) is the physical process of transition between one state of a medium and another. Commonly the term is used to refer to changes among the basic State of matter, states of matter: solid, liquid, and gas, and in rare cases, plasma (physics), plasma. A phase of a thermodynamic system and the states of matter have uniform physical property, physical properties. During a phase transition of a given medium, certain properties of the medium change as a result of the change of external conditions, such as temperature or pressure. This can be a discontinuous change; for example, a liquid may become gas upon heating to its boiling point, resulting in an abrupt change in volume. The identification of the external conditions at which a transformation occurs defines the phase transition point. Types of phase transition States of matter Phase transitions commonly refer to when a substance tran ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Central Limit Theorem
In probability theory, the central limit theorem (CLT) states that, under appropriate conditions, the Probability distribution, distribution of a normalized version of the sample mean converges to a Normal distribution#Standard normal distribution, standard normal distribution. This holds even if the original variables themselves are not Normal distribution, normally distributed. There are several versions of the CLT, each applying in the context of different conditions. The theorem is a key concept in probability theory because it implies that probabilistic and statistical methods that work for normal distributions can be applicable to many problems involving other types of distributions. This theorem has seen many changes during the formal development of probability theory. Previous versions of the theorem date back to 1811, but in its modern form it was only precisely stated as late as 1920. In statistics, the CLT can be stated as: let X_1, X_2, \dots, X_n denote a Sampling ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |