Random Generalized Lotka–Volterra Model

The random generalized Lotka–Volterra model (rGLV) is an ecological model and random set of coupled ordinary differential equations where the parameters of the generalized Lotka–Volterra equation are sampled from a probability distribution, analogously to quenched disorder. The rGLV models dynamics of a community of species in which each species' abundance grows towards a carrying capacity but is depleted due to competition from the presence of other species. It is often analyzed in the many-species limit using tools from statistical physics, in particular from spin glass theory.

The rGLV has been used as a tool to analyze emergent macroscopic behavior in microbial communities with dense, strong interspecies interactions. The model has served as a context for theoretical investigations studying diversity-stability relations in community ecology and properties of static and dynamic coexistence. Dynamical behavior in the rGLV has been mapped experimentally in community microcosms. The rGLV model has also served as an object of interest for the spin glass and disordered systems physics community to develop new techniques and numerical methods.

Definition

The random generalized Lotka–Volterra model is written as the system of coupled ordinary differential equations,$\frac = \fracN_i \left(K_i - N_i - \sum_ \alpha_ N_j\right), \qquad i = 1,\dots,S,$where $N_i$ is the abundance of species $i$, $S$ is the number of species, $K_i$ is the carrying capacity of species $i$ in the absence of interactions, $r_i$ sets a timescale, and $\alpha$ is a random matrix whose entries are random variables with mean $\langle \alpha_\rangle = \mu_\alpha/S$, variance $\mathrm(\alpha_) = \sigma_\alpha^2/S$, and correlations $\mathrm(\alpha_, \alpha_) =\gamma$ for $i \neq j$ where $-1\leq \gamma \leq 1$. The interaction matrix, $\alpha$, may be parameterized as,$\alpha_ = \frac + \frac a_,$where $a_$ are standard random variables (i.e., zero mean and unit variance) with $\langle a_ a_\rangle = \gamma$ for $i \neq j$. The matrix entries may have any distribution with common finite first and second moments and will yield identical results in the large $S$ limit due to the central limit theorem. 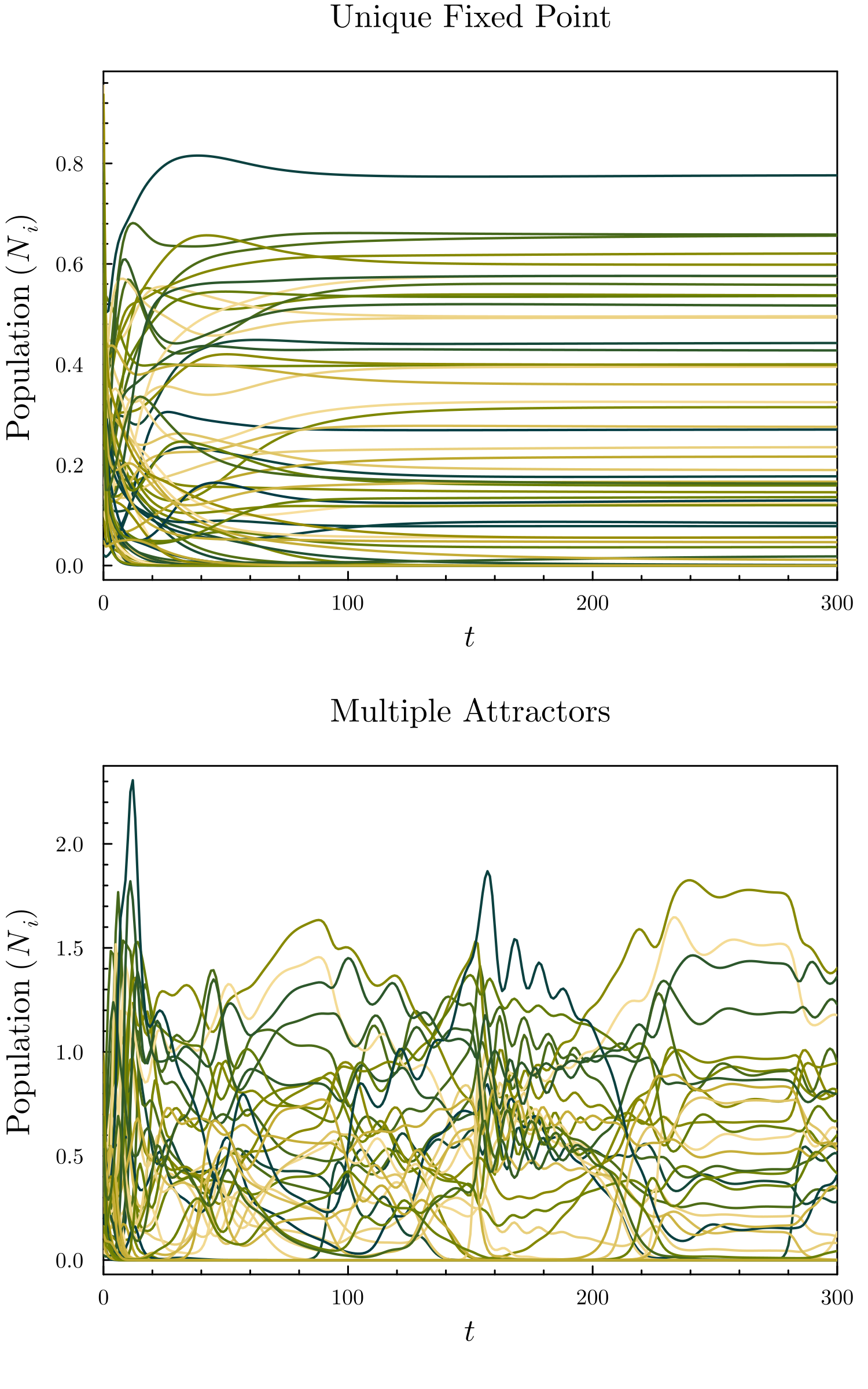The carrying capacities may also be treated as random variables with $\langle K_i \rangle = K,\,\operatorname(K_i) =\sigma_K^2.$ Analyses by statistical physics-inspired methods have revealed phase transitions between different qualitative behaviors of the model in the many-species limit. In some cases, this may include transitions between the existence of a unique globally-attractive fixed point and chaotic, persistent fluctuations.

Steady-state abundances in the thermodynamic limit

In the thermodynamic limit (i.e., the community has a very large number of species) where a unique globally-attractive fixed point exists, the distribution of species abundances can be computed using the cavity method while assuming the system is self-averaging. The self-averaging assumption means that the distribution of any one species' abundance between samplings of model parameters matches the distribution of species abundances within a single sampling of model parameters. In the cavity method, an additional mean-field species $i = 0$ is introduced and the response of the system is approximated linearly.
The cavity calculation yields a self-consistent equation describing the distribution of species abundances as a mean-field random variable, $N_0$. When $\sigma_K =0$, the mean-field equation is,$0 = N_0 \left( K - \mu_\alpha m- N_0 +\sqrt Z + \sigma_\alpha^2 \gamma\chi N_0\right),$where $m = \langle N_0\rangle ,\,q=\langle N_0^2\rangle, \,\chi = \langle \partial N_0/\partial K_0\rangle$, and $Z \sim \mathcal(0,1)$ is a standard normal random variable. Only ecologically uninvadable solutions are taken (i.e., the largest solution for $N_0$ in the quadratic equation is selected). The relevant susceptibility and moments of $N_0$, which has a truncated normal distribution, are determined self-consistently.

Dynamical phases

In the thermodynamic limit where there is an asymptotically large number of species (i.e., $S \to \infty$), there are three distinct phases: one in which there is a unique fixed point (UFP), another with a multiple attractors (MA), and a third with unbounded growth. In the MA phase, depending on whether species abundances are replenished at a small rate, may approach arbitrarily small population sizes, or are removed from the community when the population falls below some cutoff, the resulting dynamics may be chaotic with persistent fluctuations or approach an initial conditions-dependent steady state.

The transition from the UFP to MA phase is signaled by the cavity solution becoming unstable to disordered perturbations. When $\sigma_K = 0$, the phase transition boundary occurs when the parameters satisfy,$\sigma_\alpha = \frac.$In the $\sigma_K > 0$ case, the phase boundary can still be calculated analytically, but no closed-form solution has been found; numerical methods are necessary to solve the self-consistent equations determining the phase boundary.

The transition to the unbounded growth phase is signaled by the divergence of $\langle N_0 \rangle$ as computed in the cavity calculation.

Dynamical mean-field theory

The cavity method can also be used to derive a dynamical mean-field theory model for the dynamics. The cavity calculation yields a self-consistent equation describing the dynamics as a Gaussian process defined by the self-consistent equation (for $\sigma_K = 0$),\frac
=
N_0(t)
\left K_0 - N_0(t) - \mu_\alpha m(t) - \sigma_\alpha \eta(t)
+ \gamma \sigma_\alpha^2 \int_0^t\mathrm dt'\, \chi(t,t') N_0(t')
\rightwhere $m(t) = \langle N_0(t)\rangle$, $\eta$ is a zero-mean Gaussian process with autocorrelation $\langle \eta(t)\eta(t')\rangle = \langle N_0(t)N_0(t')\rangle$, and $\chi(t,t') = \langle \left.\delta N_0(t)/\delta K_0(t')\_ \rangle$ is the dynamical susceptibility defined in terms of a functional derivative of the dynamics with respect to a time-dependent perturbation of the carrying capacity.

Using dynamical mean-field theory, it has been shown that at long times, the dynamics exhibit aging in which the characteristic time scale defining the decay of correlations increases linearly in the duration of the dynamics. That is, $C_N(t,t+t\tau) \to f(\tau)$ when $t$ is large, where $C_N(t,t') = \langle N(t)N(t')\rangle$ is the autocorrelation function of the dynamics and $f(\tau)$ is a common scaling collapse function.

When a small immigration rate $\lambda \ll 1$ is added (i.e., a small constant is added to the right-hand side of the equations of motion) the dynamics reach a time transitionally invariant state. In this case, the dynamics exhibit jumps between $O(1)$ and $O(\lambda)$ abundances.

Related articles

* Generalized Lotka–Volterra equation
* Competitive Lotka–Volterra equations
* Lotka–Volterra equations
* Consumer-resource model
* Theoretical ecology
* Random dynamical system
* Spin glass
* Cavity method
* Dynamical mean-field theory
* Quenched disorder
* Community (ecology)
* Ecological stability

References

Further reading

* Stefano Allesina's Community Ecology course lecture notes: https://stefanoallesina.github.io/Theoretical_Community_Ecology/
* Bunin, Guy (2017-04-28). "Ecological communities with Lotka-Volterra dynamics". Physical Review E. 95 (4): 042414. Bibcode:2017PhRvE..95d2414B. doi:10.1103/PhysRevE.95.042414. PMID 28505745.
{{modelling ecosystems, expanded=other
Community ecology
Complex systems theory
Theoretical ecology
Random dynamical systems
Dynamical systems
Mathematical modeling
Biophysics
Ordinary differential equations
Population ecology
Ecology