|
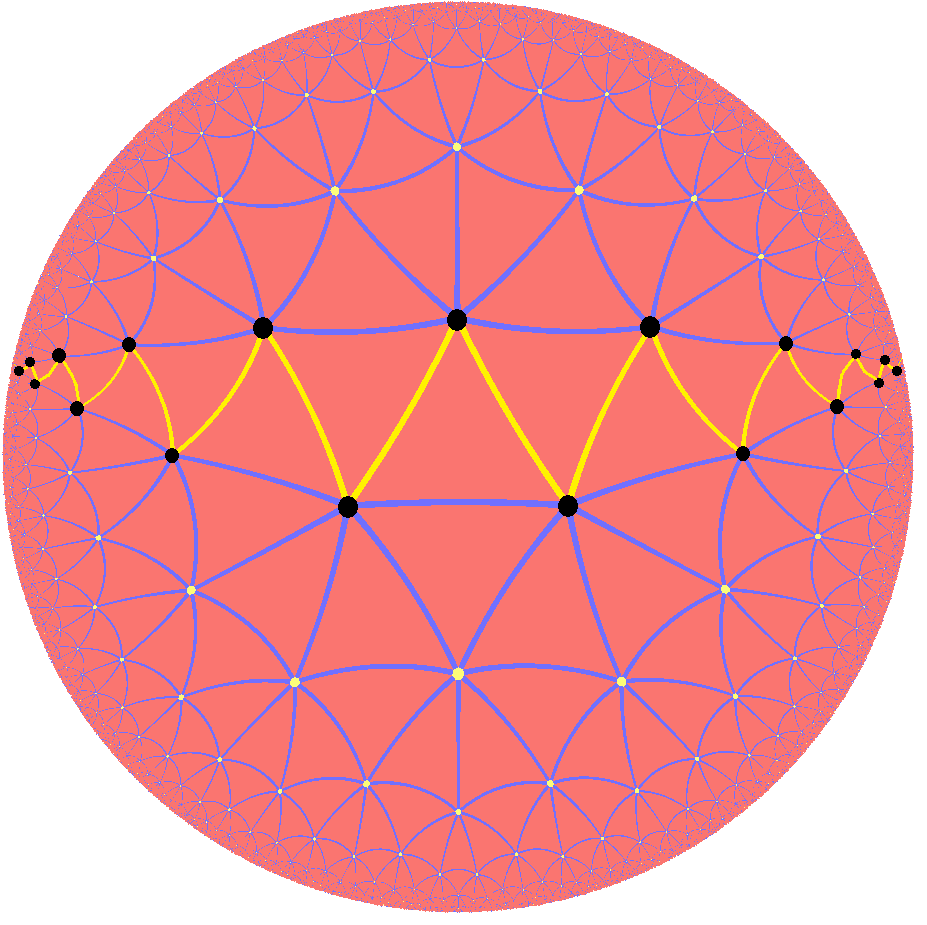
Petrie Polygon
In geometry, a Petrie polygon for a regular polytope of dimensions is a skew polygon in which every consecutive sides (but no ) belongs to one of the facets. The Petrie polygon of a regular polygon is the regular polygon itself; that of a regular polyhedron is a skew polygon such that every two consecutive sides (but no three) belongs to one of the faces. Petrie polygons are named for mathematician John Flinders Petrie. For every regular polytope there exists an orthogonal projection onto a plane such that one Petrie polygon becomes a regular polygon with the remainder of the projection interior to it. The plane in question is the Coxeter plane of the symmetry group of the polygon, and the number of sides, , is the Coxeter number of the Coxeter group. These polygons and projected graphs are useful in visualizing symmetric structure of the higher-dimensional regular polytopes. Petrie polygons can be defined more generally for any embedded graph. They form the faces of ano ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regular Dodecahedron
A regular dodecahedron or pentagonal dodecahedronStrictly speaking, a pentagonal dodecahedron need not be composed of regular pentagons. The name "pentagonal dodecahedron" therefore covers a wider class of solids than just the Platonic solid, the regular dodecahedron. is a dodecahedron composed of regular polygon, regular pentagonal faces, three meeting at each Vertex (geometry), vertex. It is an example of Platonic solids, described as cosmic stellation by Plato in his dialogues, and it was used as part of Solar System proposed by Johannes Kepler. However, the regular dodecahedron, including the other Platonic solids, has already been described by other philosophers since antiquity. The regular dodecahedron is a truncated trapezohedron because it is the result of Truncation (geometry), truncating axial vertices of a pentagonal trapezohedron. It is also a Goldberg polyhedron because it is the initial polyhedron to construct new polyhedrons by the process of chamfering. It has a re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graph Embedding
In topological graph theory, an embedding (also spelled imbedding) of a graph G on a surface \Sigma is a representation of G on \Sigma in which points of \Sigma are associated with vertices and simple arcs (homeomorphic images of ,1/math>) are associated with edges in such a way that: * the endpoints of the arc associated with an edge e are the points associated with the end vertices of e, * no arcs include points associated with other vertices, * two arcs never intersect at a point which is interior to either of the arcs. Here a surface is a connected 2-manifold. Informally, an embedding of a graph into a surface is a drawing of the graph on the surface in such a way that its edges may intersect only at their endpoints. It is well known that any finite graph can be embedded in 3-dimensional Euclidean space \mathbb^3.. A planar graph is one that can be embedded in 2-dimensional Euclidean space \mathbb^2. Often, an embedding is regarded as an equivalence class (under home ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compound Of Dodecahedron And Icosahedron
In geometry, this polyhedron can be seen as either a polyhedral stellation or a compound. As a compound It can be seen as the compound of an icosahedron and dodecahedron. It is one of four compounds constructed from a Platonic solid or Kepler-Poinsot solid, and its dual. It has icosahedral symmetry (I''h'') and the same vertex arrangement as a rhombic triacontahedron. This can be seen as the three-dimensional equivalent of the compound of two pentagons ( " decagram"); this series continues into the fourth dimension as the compound of 120-cell and 600-cell and into higher dimensions as compounds of hyperbolic tilings. As a stellation This polyhedron is the first stellation of the icosidodecahedron, and given as Wenninger model index 47. The stellation facets for construction are: : As a Faceting The compound of a Dodecahedron and an Icosahedron shares the same vertices as a list of other polyhedra, including the Rhombic triacontahedron and the Small tria ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compound Of Cube And Octahedron
The compound of cube and octahedron is a polyhedron which can be seen as either a polyhedral stellation or a Polyhedron compound, compound. Construction The 14 Cartesian coordinates of the vertices of the compound are. : 6: (±2, 0, 0), ( 0, ±2, 0), ( 0, 0, ±2) : 8: ( ±1, ±1, ±1) As a compound It can be seen as the Polyhedron compound, compound of an octahedron and a cube. It is one of four compounds constructed from a Platonic solid or Kepler-Poinsot polyhedron and its dual. It has octahedral symmetry (O''h'') and shares the same vertices as a rhombic dodecahedron. This can be seen as the three-dimensional equivalent of the compound of two squares ( "octagram"); this series continues on to infinity, with the four-dimensional equivalent being the compound of tesseract and 16-cell. As a stellation It is also the first stellation of the cuboctahedron and given as List of Wenninger polyhedron models#Stellations of cuboctahedron, Wenninger model index 43. It can ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compound Of Two Tetrahedra
The stellated octahedron is the only stellation of the octahedron. It is also called the stella octangula (Latin for "eight-pointed star"), a name given to it by Johannes Kepler in 1609, though it was known to earlier geometers. It was depicted in Pacioli's ''De Divina Proportione,'' 1509. It is the simplest of five regular polyhedral compounds, and the only regular polyhedral compound composed of only two polyhedra. It can be seen as a 3D extension of the hexagram: the hexagram is a two-dimensional shape formed from two overlapping equilateral triangles, centrally symmetric to each other, and in the same way the stellated octahedron can be formed from two centrally symmetric overlapping tetrahedra. This can be generalized to any desired amount of higher dimensions; the four-dimensional equivalent construction is the compound of two 5-cells. Construction and properties The stellated octahedron is constructed by a stellation of the regular octahedron. In other words, it ext ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Semiregular Polytope
In geometry, by Thorold Gosset's definition a semiregular polytope is usually taken to be a polytope that is vertex-transitive and has all its facets being regular polytopes. E.L. Elte compiled a longer list in 1912 as ''The Semiregular Polytopes of the Hyperspaces'' which included a wider definition. Gosset's list In three-dimensional space and below, the terms ''semiregular polytope'' and '' uniform polytope'' have identical meanings, because all uniform polygons must be regular. However, since not all uniform polyhedra are regular, the number of semiregular polytopes in dimensions higher than three is much smaller than the number of uniform polytopes in the same number of dimensions. The three convex semiregular 4-polytopes are the rectified 5-cell, snub 24-cell and rectified 600-cell. The only semiregular polytopes in higher dimensions are the ''k''21 polytopes, where the rectified 5-cell is the special case of ''k'' = 0. These were all listed by Gosset, but a proof o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regular Polytopes
''Regular Polytopes'' is a geometry book on regular polytopes written by Harold Scott MacDonald Coxeter. It was originally published by Methuen in 1947 and by Pitman Publishing in 1948, with a second edition published by Macmillan in 1963 and a third edition by Dover Publications in 1973. The Basic Library List Committee of the Mathematical Association of America has recommended that it be included in undergraduate mathematics libraries. Overview The main topics of the book are the Platonic solids (regular convex polyhedra), related polyhedra, and their higher-dimensional generalizations. It has 14 chapters, along with multiple appendices, providing a more complete treatment of the subject than any earlier work, and incorporating material from 18 of Coxeter's own previous papers. It includes many figures (both photographs of models by Paul Donchian and drawings), tables of numerical values, and historical remarks on the subject. The first chapter discusses regular polygons, regula ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
University Of Toronto
The University of Toronto (UToronto or U of T) is a public university, public research university whose main campus is located on the grounds that surround Queen's Park (Toronto), Queen's Park in Toronto, Ontario, Canada. It was founded by royal charter in 1827 as King's College, the first institution of higher learning in Upper Canada. Originally controlled by the Church of England, the university assumed its present name in 1850 upon becoming a secular institution. It has three campuses: University of Toronto Mississauga, Mississauga, #St. George campus, St. George, and University of Toronto Scarborough, Scarborough. Its main campus, St. George, is the oldest of the three and located in Downtown Toronto. U of T operates as a collegiate university, comprising 11 #Colleges, colleges, each with substantial autonomy on financial and institutional affairs and significant differences in character and history. The University of Toronto is the largest university in Canada with a t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
The Fifty-Nine Icosahedra
''The Fifty-Nine Icosahedra'' is a book written and illustrated by Harold Scott MacDonald Coxeter, H. S. M. Coxeter, Patrick du Val, P. Du Val, H. T. Flather and J. F. Petrie. It enumerates certain stellations of the regular convex or Platonic regular icosahedron, icosahedron, according to a set of rules put forward by J. C. P. Miller. First published by the University of Toronto in 1938, a Second Edition reprint by Springer-Verlag followed in 1982. Tarquin's 1999 Third Edition included new reference material and photographs by K. and D. Crennell. Authors' contributions Miller's rules Although J. C. P. Miller, Miller did not contribute to the book directly, he was a close colleague of Coxeter and Petrie. His contribution is immortalised in his set of rules for defining which stellation forms should be considered "properly significant and distinct": :''(i) The faces must lie in twenty planes, viz., the bounding planes of the regular icosahedron.'' :''(ii) All parts composing t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Patrick Du Val
Patrick du Val (March 26, 1903 – January 22, 1987) was a British mathematician, known for his work on algebraic geometry, differential geometry, and general relativity. The concept of Du Val singularity of an algebraic surface is named after him. Early life Du Val was born in Cheadle Hulme, Cheshire. He was the son of a cabinet maker, but his parents' marriage broke up. As a child, he suffered ill-health, in particular asthma, and was educated mostly by his mother. He was awarded a first class honours degree from the University of London External Programme in 1926, which he took by correspondence course. He was a talented linguist, for example teaching himself Norwegian so that he might read Peer Gynt. He also had a strong interest in history but his love of mathematics led him to pursue that as a career. His earliest publications show a leaning towards applied mathematics. His mother moved to a village near Cambridge and he became acquainted with Henry Baker, Low ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Proceedings Of The London Mathematical Society
The London Mathematical Society (LMS) is one of the United Kingdom's learned societies for mathematics (the others being the Royal Statistical Society (RSS), the Institute of Mathematics and its Applications (IMA), the Edinburgh Mathematical Society and the Operational Research Society (ORS). History The Society was established on 16 January 1865, the first president being Augustus De Morgan. The earliest meetings were held in University College, but the Society soon moved into Burlington House, Piccadilly. The initial activities of the Society included talks and publication of a journal. The LMS was used as a model for the establishment of the American Mathematical Society in 1888. Mary Cartwright was the first woman to be President of the LMS (in 1961–62). The Society was granted a royal charter in 1965, a century after its foundation. In 1998 the Society moved from rooms in Burlington House into De Morgan House (named after the society's first president), at 57–5 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sir W
''Sir'' is a formal honorific address in English for men, derived from Sire in the High Middle Ages. Both are derived from the old French "" (Lord), brought to England by the French-speaking Normans, and which now exist in French only as part of "", with the equivalent "My Lord" in English. Traditionally, as governed by law and custom, Sir is used for men who are knights and belong to certain orders of chivalry, as well as later applied to baronets and other offices. As the female equivalent for knighthood is damehood, the ''suo jure'' female equivalent term is typically Dame. The wife of a knight or baronet tends to be addressed as Lady, although a few exceptions and interchanges of these uses exist. Additionally, since the late modern period, Sir has been used as a respectful way to address a man of superior social status or military rank. Equivalent terms of address for women are Madam (shortened to Ma'am), in addition to social honorifics such as Mrs, Ms, or Miss. E ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |