Compound Of Two Tetrahedra on:
[Wikipedia]
[Google]
[Amazon]
 The stellated octahedron is the only
The stellated octahedron is the only
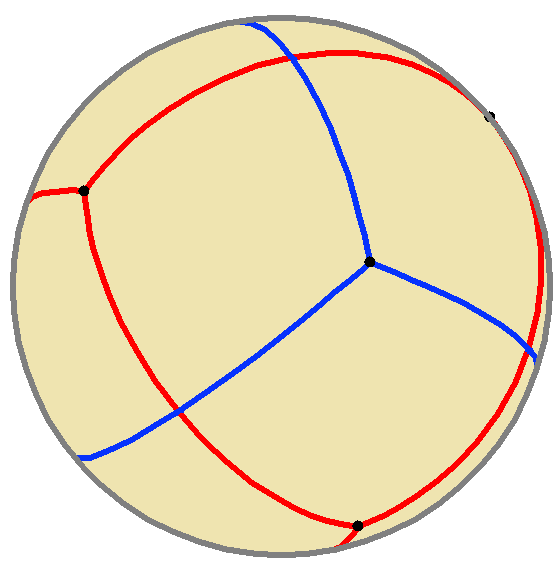 A compound of two spherical tetrahedra can be constructed, as illustrated.
The two tetrahedra of the compound view of the stellated octahedron are "desmic", meaning that (when interpreted as a line in
A compound of two spherical tetrahedra can be constructed, as illustrated.
The two tetrahedra of the compound view of the stellated octahedron are "desmic", meaning that (when interpreted as a line in
stellation
In geometry, stellation is the process of extending a polygon in two dimensions, a polyhedron in three dimensions, or, in general, a polytope in ''n'' dimensions to form a new figure. Starting with an original figure, the process extends specific ...
of the octahedron
In geometry, an octahedron (: octahedra or octahedrons) is any polyhedron with eight faces. One special case is the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex. Many types of i ...
. It is also called the stella octangula (Latin for "eight-pointed star"), a name given to it by Johannes Kepler
Johannes Kepler (27 December 1571 – 15 November 1630) was a German astronomer, mathematician, astrologer, Natural philosophy, natural philosopher and writer on music. He is a key figure in the 17th-century Scientific Revolution, best know ...
in 1609, though it was known to earlier geometers. It was depicted in Pacioli
Luca Bartolomeo de Pacioli, Order of Friars Minor, O.F.M. (sometimes ''Paccioli'' or ''Paciolo''; 1447 – 19 June 1517) was an Italian mathematician, Order of Friars Minor, Franciscan friar, collaborator with Leonardo da Vinci, and an early c ...
's ''De Divina Proportione
''Divina proportione'' (15th century Italian for ''Divine proportion''), later also called ''De divina proportione'' (converting the Italian title into a Latin one) is a book on mathematics written by Luca Pacioli and illustrated by Leonardo da V ...
,'' 1509.
It is the simplest of five regular polyhedral compound
In geometry, a polyhedral compound is a figure that is composed of several polyhedra sharing a common Centroid, centre. They are the three-dimensional analogs of star polygon#Regular compounds, polygonal compounds such as the hexagram.
The oute ...
s, and the only regular polyhedral compound composed of only two polyhedra.
It can be seen as a 3D extension of the hexagram
, can be seen as a compound polygon, compound composed of an upwards (blue here) and downwards (pink) facing equilateral triangle, with their intersection as a regular hexagon (in green).
A hexagram (Greek language, Greek) or sexagram (Latin l ...
: the hexagram is a two-dimensional shape formed from two overlapping equilateral triangles, centrally symmetric to each other, and in the same way the stellated octahedron can be formed from two centrally symmetric overlapping tetrahedra. This can be generalized to any desired amount of higher dimensions; the four-dimensional equivalent construction is the compound of two 5-cells
In geometry, the 5-cell is the convex 4-polytope with Schläfli symbol . It is a 5-vertex four-dimensional object bounded by five tetrahedral cells. It is also known as a C5, hypertetrahedron, pentachoron, pentatope, pentahedroid, tetrahedral ...
.
Construction and properties
The stellated octahedron is constructed by astellation
In geometry, stellation is the process of extending a polygon in two dimensions, a polyhedron in three dimensions, or, in general, a polytope in ''n'' dimensions to form a new figure. Starting with an original figure, the process extends specific ...
of the regular octahedron
In geometry, a regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex. Regular octahedra occur in nature as crystal structures. An octahedron, more generally, can be any eight-sided polyh ...
. In other words, it extends to form equilateral triangles on each regular octahedron's faces. Magnus Wenninger
Father Magnus J. Wenninger OSB (October 31, 1919Banchoff (2002)– February 17, 2017) was an American mathematician who worked on constructing polyhedron models, and wrote the first book on their construction.
Early life and education
Born to ...
's ''Polyhedron Models'' denote this model as nineteenth W19.
The stellated octahedron is a faceting
Stella octangula as a faceting of the cube
In geometry, faceting (also spelled facetting) is the process of removing parts of a polygon, polyhedron or polytope, without creating any new Vertex (geometry), vertices.
New edges of a faceted po ...
of the cube
A cube or regular hexahedron is a three-dimensional space, three-dimensional solid object in geometry, which is bounded by six congruent square (geometry), square faces, a type of polyhedron. It has twelve congruent edges and eight vertices. It i ...
, meaning removing part of the polygonal faces without creating new vertices of a cube. The symmetry operation of a stellated octahedron has the same one as the cube. Hence, its three-dimensional point group symmetry is an octahedral symmetry
A regular octahedron has 24 rotational (or orientation-preserving) symmetries, and 48 symmetries altogether. These include transformations that combine a reflection and a rotation. A cube has the same set of symmetries, since it is the polyhedr ...
.
The stellated octahedron is also a regular polyhedron compound, when constructed as the union of two regular tetrahedra
In geometry, a tetrahedron (: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular Face (geometry), faces, six straight Edge (geometry), edges, and four vertex (geometry), vertices. The tet ...
. Hence, the stellated octahedron is also called "compound of two tetrahedra". The two tetrahedra share a common intersphere in the centre, making the compound self-dual. There exist compositions of all symmetries of tetrahedra reflected about the cube's center, so the stellated octahedron may also have pyritohedral symmetry.
The stellated octahedron can be obtained as an augmentation of the regular octahedron
In geometry, an octahedron (: octahedra or octahedrons) is any polyhedron with eight faces. One special case is the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex. Many types of i ...
, by adding tetrahedral pyramids
A pyramid () is a Nonbuilding structure, structure whose visible surfaces are triangular in broad outline and converge toward the top, making the appearance roughly a Pyramid (geometry), pyramid in the geometric sense. The base of a pyramid ca ...
on each face. This results in that its volume is the sum of eight tetrahedrons' and one regular octahedron's volume, times of the side length. However, this construction is topologically similar as the Catalan solid
The Catalan solids are the dual polyhedron, dual polyhedra of Archimedean solids. The Archimedean solids are thirteen highly-symmetric polyhedra with regular faces and symmetric vertices. The faces of the Catalan solids correspond by duality to ...
of a triakis octahedron
In geometry, a triakis octahedron (or trigonal trisoctahedron or kisoctahedronConway, Symmetries of things, p. 284) is an Archimedean solid, Archimedean dual solid, or a Catalan solid. Its dual is the truncated cube.
It can be seen as an octahedr ...
with much shorter pyramids, known as the Kleetope of an octahedron.
It can be seen as a antiprism
In geometry, an antiprism or is a polyhedron composed of two Parallel (geometry), parallel Euclidean group, direct copies (not mirror images) of an polygon, connected by an alternating band of triangles. They are represented by the Conway po ...
; with being a tetragram, a compound of two dual digon
In geometry, a bigon, digon, or a ''2''-gon, is a polygon with two sides (edge (geometry), edges) and two Vertex (geometry), vertices. Its construction is Degeneracy (mathematics), degenerate in a Euclidean plane because either the two sides wou ...
s, and the tetrahedron seen as a digonal antiprism, this can be seen as a compound of two digonal antiprisms.
It can be seen as a net of a four-dimensional octahedral pyramid, consisting of a central octahedron surrounded by eight tetrahedra.
Related concepts
 A compound of two spherical tetrahedra can be constructed, as illustrated.
The two tetrahedra of the compound view of the stellated octahedron are "desmic", meaning that (when interpreted as a line in
A compound of two spherical tetrahedra can be constructed, as illustrated.
The two tetrahedra of the compound view of the stellated octahedron are "desmic", meaning that (when interpreted as a line in projective space
In mathematics, the concept of a projective space originated from the visual effect of perspective, where parallel lines seem to meet ''at infinity''. A projective space may thus be viewed as the extension of a Euclidean space, or, more generally ...
) each edge of one tetrahedron crosses two opposite edges of the other tetrahedron. One of these two crossings is visible in the stellated octahedron; the other crossing occurs at a point at infinity of the projective space, where each edge of one tetrahedron crosses the parallel edge of the other tetrahedron. These two tetrahedra can be completed to a desmic system of three tetrahedra, where the third tetrahedron has as its four vertices the three crossing points at infinity and the centroid of the two finite tetrahedra. The same twelve tetrahedron vertices also form the points of Reye's configuration.
The stella octangula numbers are figurate numbers that count the number of balls that can be arranged into the shape of a stellated octahedron. These numbers are the form of for being the positive integers; the first ten such numbers are:
:0, 1, 14, 51, 124, 245, 426, 679, 1016, 1449, 1990, ....
In popular culture
The stellated octahedron appears with several other polyhedra and polyhedral compounds inM. C. Escher
Maurits Cornelis Escher (; ; 17 June 1898 – 27 March 1972) was a Dutch graphic artist who made woodcuts, lithography, lithographs, and mezzotints, many of which were Mathematics and art, inspired by mathematics.
Despite wide popular int ...
's print "Stars
A star is a luminous spheroid of plasma held together by self-gravity. The nearest star to Earth is the Sun. Many other stars are visible to the naked eye at night; their immense distances from Earth make them appear as fixed points of ...
", and provides the central form in Escher's ''Double Planetoid
''Double Planetoid'' is a wood engraving print by the Dutch artist M. C. Escher, first printed in 1949.
Description
''Double Planetoid'' is printed in four colors from four wood blocks. It depicts a Minor planet, planetoid in the shape of a com ...
'' (1949).
The obelisk in the center of the in Zaragoza
Zaragoza (), traditionally known in English as Saragossa ( ), is the capital city of the province of Zaragoza and of the autonomous communities of Spain, autonomous community of Aragon, Spain. It lies by the Ebro river and its tributaries, the ...
, Spain
Spain, or the Kingdom of Spain, is a country in Southern Europe, Southern and Western Europe with territories in North Africa. Featuring the Punta de Tarifa, southernmost point of continental Europe, it is the largest country in Southern Eur ...
, is surrounded by twelve stellated octahedral lampposts, shaped to form a three-dimensional version of the Flag of Europe
The flag of Europe or European flag consists of twelve Or (heraldry), golden stars forming a Circle of stars, circle on a Azure (heraldry), blue field. It was designed and adopted in 1955 by the Council of Europe (CoE) as a symbol for the who ...
.
Some modern mystics have associated this shape with the "merkaba", which according to them is a "counter-rotating energy field" named from an ancient Egyptian word. However, the word "merkaba" is actually Hebrew
Hebrew (; ''ʿÎbrit'') is a Northwest Semitic languages, Northwest Semitic language within the Afroasiatic languages, Afroasiatic language family. A regional dialect of the Canaanite languages, it was natively spoken by the Israelites and ...
, and more properly refers to a chariot
A chariot is a type of vehicle similar to a cart, driven by a charioteer, usually using horses to provide rapid Propulsion, motive power. The oldest known chariots have been found in burials of the Sintashta culture in modern-day Chelyabinsk O ...
in the visions of Ezekiel
Ezekiel, also spelled Ezechiel (; ; ), was an Israelite priest. The Book of Ezekiel, relating his visions and acts, is named after him.
The Abrahamic religions acknowledge Ezekiel as a prophet. According to the narrative, Ezekiel prophesied ...
.
The resemblance between this shape and the two-dimensional star of David
The Star of David (, , ) is a symbol generally recognized as representing both Jewish identity and Judaism. Its shape is that of a hexagram: the compound of two equilateral triangles.
A derivation of the Seal of Solomon was used for decora ...
has also been frequently noted.
References
External links
* *{{KlitzingPolytopes, ../incmats/so.htm, 3D compound, mode=cs2 Polyhedral compounds Polyhedral stellation Sacred geometry