|
Partial Regression Plot
In applied statistics, a partial regression plot attempts to show the effect of adding another variable to a model that already has one or more independent variables. Partial regression plots are also referred to as added variable plots, adjusted variable plots, and individual coefficient plots. When performing a linear regression with a single independent variable, a scatter plot of the response variable against the independent variable provides a good indication of the nature of the relationship. If there is more than one independent variable, things become more complicated. Although it can still be useful to generate scatter plots of the response variable against each of the independent variables, this does not take into account the effect of the other independent variables in the model. Calculation Partial regression plots are formed by: #Computing the residuals of regressing the response variable against the independent variables but omitting ''X''i #Computing the residuals f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Applied Statistics
Statistics (from German: ''Statistik'', "description of a state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of surveys and experiments.Dodge, Y. (2006) ''The Oxford Dictionary of Statistical Terms'', Oxford University Press. When census data cannot be collected, statisticians collect data by developing specific experiment designs and survey samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample to the population as a whole. An experim ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Regression
In statistics, linear regression is a linear approach for modelling the relationship between a scalar response and one or more explanatory variables (also known as dependent and independent variables). The case of one explanatory variable is called '' simple linear regression''; for more than one, the process is called multiple linear regression. This term is distinct from multivariate linear regression, where multiple correlated dependent variables are predicted, rather than a single scalar variable. In linear regression, the relationships are modeled using linear predictor functions whose unknown model parameters are estimated from the data. Such models are called linear models. Most commonly, the conditional mean of the response given the values of the explanatory variables (or predictors) is assumed to be an affine function of those values; less commonly, the conditional median or some other quantile is used. Like all forms of regression analysis, linear regressio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Independent Variable
Dependent and independent variables are variables in mathematical modeling, statistical modeling and experimental sciences. Dependent variables receive this name because, in an experiment, their values are studied under the supposition or demand that they depend, by some law or rule (e.g., by a mathematical function), on the values of other variables. Independent variables, in turn, are not seen as depending on any other variable in the scope of the experiment in question. In this sense, some common independent variables are time, space, density, mass, fluid flow rate, and previous values of some observed value of interest (e.g. human population size) to predict future values (the dependent variable). Of the two, it is always the dependent variable whose variation is being studied, by altering inputs, also known as regressors in a statistical context. In an experiment, any variable that can be attributed a value without attributing a value to any other variable is called an in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Scatter Plot
A scatter plot (also called a scatterplot, scatter graph, scatter chart, scattergram, or scatter diagram) is a type of plot or mathematical diagram using Cartesian coordinates to display values for typically two variables for a set of data. If the points are coded (color/shape/size), one additional variable can be displayed. The data are displayed as a collection of points, each having the value of one variable determining the position on the horizontal axis and the value of the other variable determining the position on the vertical axis. Overview A scatter plot can be used either when one continuous variable is under the control of the experimenter and the other depends on it or when both continuous variables are independent. If a parameter exists that is systematically incremented and/or decremented by the other, it is called the ''control parameter'' or independent variable and is customarily plotted along the horizontal axis. The measured or dependent variable is cu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Response Variable
Dependent and independent variables are variables in mathematical modeling, statistical modeling and experimental sciences. Dependent variables receive this name because, in an experiment, their values are studied under the supposition or demand that they depend, by some law or rule (e.g., by a mathematical function), on the values of other variables. Independent variables, in turn, are not seen as depending on any other variable in the scope of the experiment in question. In this sense, some common independent variables are time, space, density, mass, fluid flow rate, and previous values of some observed value of interest (e.g. human population size) to predict future values (the dependent variable). Of the two, it is always the dependent variable whose variation is being studied, by altering inputs, also known as regressors in a statistical context. In an experiment, any variable that can be attributed a value without attributing a value to any other variable is called an ind ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
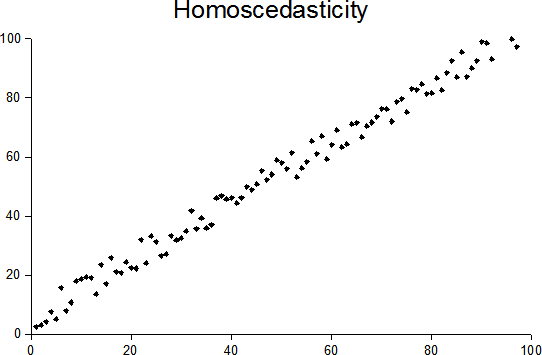
Heteroscedasticity
In statistics, a sequence (or a vector) of random variables is homoscedastic () if all its random variables have the same finite variance. This is also known as homogeneity of variance. The complementary notion is called heteroscedasticity. The spellings ''homoskedasticity'' and ''heteroskedasticity'' are also frequently used. Assuming a variable is homoscedastic when in reality it is heteroscedastic () results in unbiased but inefficient point estimates and in biased estimates of standard errors, and may result in overestimating the goodness of fit as measured by the Pearson coefficient. The existence of heteroscedasticity is a major concern in regression analysis and the analysis of variance, as it invalidates statistical tests of significance that assume that the modelling errors all have the same variance. While the ordinary least squares estimator is still unbiased in the presence of heteroscedasticity, it is inefficient and generalized least squares should be used i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partial Residual Plot
In applied statistics, a partial residual plot is a graphical technique that attempts to show the relationship between a given independent variable and the response variable given that other independent variables are also in the model. Background When performing a linear regression with a single independent variable, a scatter plot of the response variable against the independent variable provides a good indication of the nature of the relationship. If there is more than one independent variable, things become more complicated. Although it can still be useful to generate scatter plots of the response variable against each of the independent variables, this does not take into account the effect of the other independent variables in the model. Definition Partial residual plots are formed as : \text + \hat_iX_i \text X_i, where : Residuals = residuals from the full model, : \hat_i = regression coefficient from the ''i''-th independent variable in the full model, : ''X''i = the '' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Leverage (statistics)
In statistics and in particular in regression analysis, leverage is a measure of how far away the independent variable values of an observation are from those of the other observations. ''High-leverage points'', if any, are outliers with respect to the independent variables. That is, high-leverage points have no neighboring points in \mathbb^ space, where '''' is the number of independent variables in a regression model. This makes the fitted model likely to pass close to a high leverage observation. Hence high-leverage points have the potential to cause large changes in the parameter estimates when they are deleted i.e., to be influential points. Although an influential point will typically have high leverage, a high leverage point is not necessarily an influential point. The leverage is typically defined as the diagonal elements of the hat matrix. Definition and interpretations Consider the linear regression model _i = \boldsymbol_i^\boldsymbol+_i, i=1,\, 2,\ldots,\, n. That ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Simple Correlation
In statistics, correlation or dependence is any statistical relationship, whether causal or not, between two random variables or bivariate data. Although in the broadest sense, "correlation" may indicate any type of association, in statistics it usually refers to the degree to which a pair of variables are '' linearly'' related. Familiar examples of dependent phenomena include the correlation between the height of parents and their offspring, and the correlation between the price of a good and the quantity the consumers are willing to purchase, as it is depicted in the so-called demand curve. Correlations are useful because they can indicate a predictive relationship that can be exploited in practice. For example, an electrical utility may produce less power on a mild day based on the correlation between electricity demand and weather. In this example, there is a causal relationship, because extreme weather causes people to use more electricity for heating or cooling. Howe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partial Correlation
In probability theory and statistics, partial correlation measures the degree of association between two random variables, with the effect of a set of controlling random variables removed. When determining the numerical relationship between two variables of interest, using their correlation coefficient will give misleading results if there is another confounding variable that is numerically related to both variables of interest. This misleading information can be avoided by controlling for the confounding variable, which is done by computing the partial correlation coefficient. This is precisely the motivation for including other right-side variables in a multiple regression; but while multiple regression gives unbiased results for the effect size, it does not give a numerical value of a measure of the strength of the relationship between the two variables of interest. For example, given economic data on the consumption, income, and wealth of various individuals, consider th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partial Residual Plot
In applied statistics, a partial residual plot is a graphical technique that attempts to show the relationship between a given independent variable and the response variable given that other independent variables are also in the model. Background When performing a linear regression with a single independent variable, a scatter plot of the response variable against the independent variable provides a good indication of the nature of the relationship. If there is more than one independent variable, things become more complicated. Although it can still be useful to generate scatter plots of the response variable against each of the independent variables, this does not take into account the effect of the other independent variables in the model. Definition Partial residual plots are formed as : \text + \hat_iX_i \text X_i, where : Residuals = residuals from the full model, : \hat_i = regression coefficient from the ''i''-th independent variable in the full model, : ''X''i = the '' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partial Leverage Plot
In regression analysis, partial leverage (PL) is a measure of the contribution of the individual independent variables to the total leverage of each observation. That is, if ''h''''i'' is the ''i''th element of the diagonal of the hat matrix, PL is a measure of how ''h''''i'' changes as a variable is added to the regression model. It is computed as: : \left(\mathrm_j\right)_i = \frac where :''j'' = index of independent variable :''i'' = index of observation :''X''''j''· 'j''/sub> = residuals from regressing ''X''''j'' against the remaining independent variables Note that the partial leverage is the leverage of the ''i''th point in the partial regression plot for the ''j''th variable. Data points with large partial leverage for an independent variable can exert undue influence on the selection of that variable in automatic regression model building procedures. See also * Leverage * Partial residual plot * Partial regression plot * Variance inflation factor for a multi- ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |