 |
Parallel Single-source Shortest Path Algorithm
A central problem in algorithmic graph theory is the shortest path problem. One of the generalizations of the shortest path problem is known as the single-source-shortest-paths (SSSP) problem, which consists of finding the shortest path between every pair of vertices in a graph. There are classical sequential algorithms which solve this problem, such as Dijkstra's algorithm. In this article, however, we present two parallel algorithms solving this problem. Another variation of the problem is the all-pairs-shortest-paths (APSP) problem, which also has parallel approaches: Parallel all-pairs shortest path algorithm. Problem definition Let G=(V,E) be a directed graph with , V, =n nodes and , E, =m edges. Let s be a distinguished vertex (called "source") and c be a function assigning a non-negative real-valued weight to each edge. The goal of the single-source-shortest-paths problem is to compute, for every vertex v reachable from s, the weight of a minimum-weight path from s to v, d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Graph Theory
In mathematics, graph theory is the study of '' graphs'', which are mathematical structures used to model pairwise relations between objects. A graph in this context is made up of '' vertices'' (also called ''nodes'' or ''points'') which are connected by ''edges'' (also called ''links'' or ''lines''). A distinction is made between undirected graphs, where edges link two vertices symmetrically, and directed graphs, where edges link two vertices asymmetrically. Graphs are one of the principal objects of study in discrete mathematics. Definitions Definitions in graph theory vary. The following are some of the more basic ways of defining graphs and related mathematical structures. Graph In one restricted but very common sense of the term, a graph is an ordered pair G=(V,E) comprising: * V, a set of vertices (also called nodes or points); * E \subseteq \, a set of edges (also called links or lines), which are unordered pairs of vertices (that is, an edge is associated with t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Shortest Path Problem
In graph theory, the shortest path problem is the problem of finding a path between two vertices (or nodes) in a graph such that the sum of the weights of its constituent edges is minimized. The problem of finding the shortest path between two intersections on a road map may be modeled as a special case of the shortest path problem in graphs, where the vertices correspond to intersections and the edges correspond to road segments, each weighted by the length of the segment. Definition The shortest path problem can be defined for graphs whether undirected, directed, or mixed. It is defined here for undirected graphs; for directed graphs the definition of path requires that consecutive vertices be connected by an appropriate directed edge. Two vertices are adjacent when they are both incident to a common edge. A path in an undirected graph is a sequence of vertices P = ( v_1, v_2, \ldots, v_n ) \in V \times V \times \cdots \times V such that v_i is adjacent to v_ for 1 \le ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Sequential Algorithm
In computer science, a sequential algorithm or serial algorithm is an algorithm that is executed sequentially – once through, from start to finish, without other processing executing – as opposed to concurrently or in parallel. The term is primarily used to contrast with '' concurrent algorithm'' or '' parallel algorithm;'' most standard computer algorithms are sequential algorithms, and not specifically identified as such, as sequentialness is a background assumption. Concurrency and parallelism are in general distinct concepts, but they often overlap – many distributed algorithms are both concurrent and parallel – and thus "sequential" is used to contrast with both, without distinguishing which one. If these need to be distinguished, the opposing pairs sequential/concurrent and serial/parallel may be used. "Sequential algorithm" may also refer specifically to an algorithm for decoding a convolutional code. See also * Online algorithm * Streaming algorithm In computer ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Dijkstra's Algorithm
Dijkstra's algorithm ( ) is an algorithm for finding the shortest paths between nodes in a graph, which may represent, for example, road networks. It was conceived by computer scientist Edsger W. Dijkstra in 1956 and published three years later. The algorithm exists in many variants. Dijkstra's original algorithm found the shortest path between two given nodes, but a more common variant fixes a single node as the "source" node and finds shortest paths from the source to all other nodes in the graph, producing a shortest-path tree. For a given source node in the graph, the algorithm finds the shortest path between that node and every other. It can also be used for finding the shortest paths from a single node to a single destination node by stopping the algorithm once the shortest path to the destination node has been determined. For example, if the nodes of the graph represent cities and edge path costs represent driving distances between pairs of cities connected by a d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Parallel Algorithm
In computer science, a parallel algorithm, as opposed to a traditional serial algorithm, is an algorithm which can do multiple operations in a given time. It has been a tradition of computer science to describe serial algorithms in abstract machine models, often the one known as random-access machine. Similarly, many computer science researchers have used a so-called parallel random-access machine (PRAM) as a parallel abstract machine (shared-memory). Many parallel algorithms are executed concurrently – though in general concurrent algorithms are a distinct concept – and thus these concepts are often conflated, with which aspect of an algorithm is parallel and which is concurrent not being clearly distinguished. Further, non-parallel, non-concurrent algorithms are often referred to as " sequential algorithms", by contrast with concurrent algorithms. Parallelizability Algorithms vary significantly in how parallelizable they are, ranging from easily parallelizable to complet ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
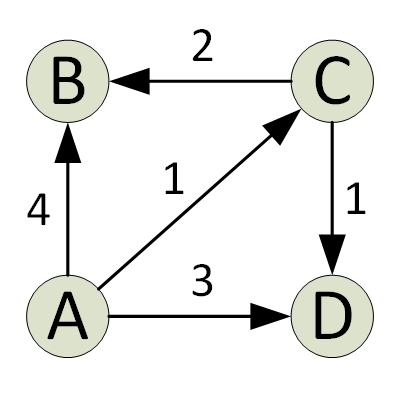 |
Parallel All-pairs Shortest Path Algorithm
A central problem in algorithmic graph theory is the shortest path problem. Hereby, the problem of finding the shortest path between every pair of nodes is known as all-pair-shortest-paths (APSP) problem. As sequential algorithms for this problem often yield long runtimes, parallelization has shown to be beneficial in this field. In this article two efficient algorithms solving this problem are introduced. Another variation of the problem is the single-source-shortest-paths (SSSP) problem, which also has parallel approaches: Parallel single-source shortest path algorithm. Problem definition Let G=(V,E,w) be a directed Graph with the set of nodes V and the set of edges E\subseteq V\times V. Each edge e \in E has a weight w(e) assigned. The goal of the all-pair-shortest-paths problem is to find the shortest path between all pairs of nodes of the graph. For this path to be unique it is required that the graph does not contain cycles with a negative weight. In the remainder of the a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Parallel Random-access Machine
In computer science, a parallel random-access machine (parallel RAM or PRAM) is a shared-memory abstract machine. As its name indicates, the PRAM is intended as the parallel-computing analogy to the random-access machine (RAM) (not to be confused with random-access memory). In the same way that the RAM is used by sequential-algorithm designers to model algorithmic performance (such as time complexity), the PRAM is used by parallel-algorithm designers to model parallel algorithmic performance (such as time complexity, where the number of processors assumed is typically also stated). Similar to the way in which the RAM model neglects practical issues, such as access time to cache memory versus main memory, the PRAM model neglects such issues as synchronization and communication, but provides any (problem-size-dependent) number of processors. Algorithm cost, for instance, is estimated using two parameters O(time) and O(time × processor_number). Read/write conflicts Read/write conf ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
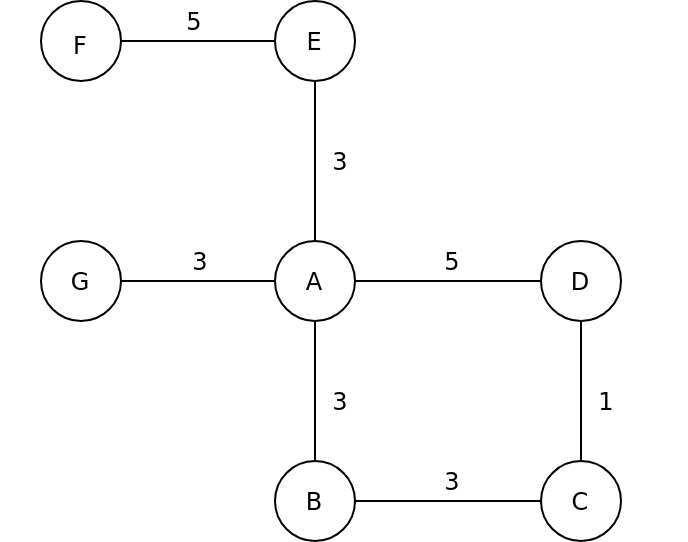
Delta Stepping Example Graph
Delta commonly refers to: * Delta (letter) (Δ or δ), a letter of the Greek alphabet * River delta, at a river mouth * D (NATO phonetic alphabet: "Delta") * Delta Air Lines, US * Delta variant of SARS-CoV-2 that causes COVID-19 Delta may also refer to: Places Canada * Delta, British Columbia ** Delta (electoral district), a federal electoral district ** Delta (provincial electoral district) * Delta, Ontario United States * Mississippi Delta * Delta, Alabama * Delta Junction, Alaska * Delta, Colorado * Delta, Illinois * Delta, Iowa * Delta, Kentucky * Delta, Louisiana * Delta, Missouri * Delta, North Carolina * Delta, Ohio * Delta, Pennsylvania * Sacramento–San Joaquin River Delta, California * Delta, Utah * Delta, Wisconsin, a town * Delta (community), Wisconsin * Delta County (other) Elsewhere * Delta Island, Antarctica * Delta Stream, Antarctica * Delta, Minas Gerais, Brazil * Nile Delta, Egypt * Delta, Thessaloniki, Greece * Delta State, Nigeria * Delta, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Graph500
The Graph500 is a rating of supercomputer systems, focused on data-intensive loads. The project was announced on International Supercomputing Conference in June 2010. The first list was published at the ACM/IEEE Supercomputing Conference in November 2010. New versions of the list are published twice a year. The main performance metric used to rank the supercomputers is GTEPS (giga- traversed edges per second). Richard Murphy from Sandia National Laboratories, says that "The Graph500's goal is to promote awareness of complex data problems", instead of focusing on computer benchmarks like HPL (High Performance Linpack), which TOP500 is based on. Despite its name, there were several hundreds of systems in the rating, growing up to 174 in June 2014. The algorithm and implementation that won the championship is published in the paper titled "Extreme scale breadth-first search on supercomputers". There is also list Green Graph 500, which uses same performance metric, but sorts li ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Breadth-first Search
Breadth-first search (BFS) is an algorithm for searching a tree data structure for a node that satisfies a given property. It starts at the tree root and explores all nodes at the present depth prior to moving on to the nodes at the next depth level. Extra memory, usually a queue, is needed to keep track of the child nodes that were encountered but not yet explored. For example, in a chess endgame a chess engine may build the game tree from the current position by applying all possible moves, and use breadth-first search to find a win position for white. Implicit trees (such as game trees or other problem-solving trees) may be of infinite size; breadth-first search is guaranteed to find a solution node if one exists. In contrast, (plain) depth-first search, which explores the node branch as far as possible before backtracking and expanding other nodes, may get lost in an infinite branch and never make it to the solution node. Iterative deepening depth-first search avoid ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Bellman–Ford Algorithm
The Bellman–Ford algorithm is an algorithm that computes shortest paths from a single source vertex to all of the other vertices in a weighted digraph. It is slower than Dijkstra's algorithm for the same problem, but more versatile, as it is capable of handling graphs in which some of the edge weights are negative numbers. The algorithm was first proposed by , but is instead named after Richard Bellman and Lester Ford Jr., who published it in 1958 and 1956, respectively. Edward F. Moore also published a variation of the algorithm in 1959, and for this reason it is also sometimes called the Bellman–Ford–Moore algorithm. Negative edge weights are found in various applications of graphs, hence the usefulness of this algorithm. If a graph contains a "negative cycle" (i.e. a cycle whose edges sum to a negative value) that is reachable from the source, then there is no ''cheapest'' path: any path that has a point on the negative cycle can be made cheaper by one more walk ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |