Parallel all-pairs shortest path algorithm on:
[Wikipedia]
[Google]
[Amazon]
A central problem in algorithmic
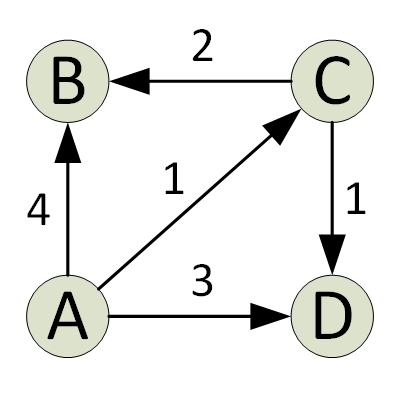
 If more than processors shall be used for the parallelization, it is required that multiple processors take part of the
If more than processors shall be used for the parallelization, it is required that multiple processors take part of the
graph theory
In mathematics, graph theory is the study of '' graphs'', which are mathematical structures used to model pairwise relations between objects. A graph in this context is made up of '' vertices'' (also called ''nodes'' or ''points'') which are conn ...
is the shortest path problem
In graph theory, the shortest path problem is the problem of finding a path between two vertices (or nodes) in a graph such that the sum of the weights of its constituent edges is minimized.
The problem of finding the shortest path between t ...
. Hereby, the problem of finding the shortest path between every pair of nodes is known as all-pair-shortest-paths (APSP) problem. As sequential algorithm In computer science, a sequential algorithm or serial algorithm is an algorithm that is executed sequentially – once through, from start to finish, without other processing executing – as opposed to concurrently or in parallel. The term is pri ...
s for this problem often yield long runtimes, parallelization has shown to be beneficial in this field. In this article two efficient algorithms solving this problem are introduced.
Another variation of the problem is the single-source-shortest-paths (SSSP) problem, which also has parallel approaches: Parallel single-source shortest path algorithm.
Problem definition
Let be a directed Graph with the set of nodes and the set of edges . Each edge has a weight assigned. The goal of the all-pair-shortest-paths problem is to find the shortest path between all pairs of nodes of the graph. For this path to be unique it is required that the graph does not contain cycles with a negative weight. In the remainder of the article it is assumed that the graph is represented using anadjacency matrix
In graph theory and computer science, an adjacency matrix is a square matrix used to represent a finite graph. The elements of the matrix indicate whether pairs of vertices are adjacent or not in the graph.
In the special case of a finite simple ...
. We expect the output of the algorithm to be a distancematrix . In , every entry is the weight of the shortest path in from node to node .
The Floyd algorithm presented later can handle negative edge weights, whereas the Dijkstra algorithm requires all edges to have a positive weight.
Dijkstra algorithm
The Dijkstra algorithm originally was proposed as a solver for the single-source-shortest-paths problem. However, the algorithm can easily be used for solving the All-Pair-Shortest-Paths problem by executing the Single-Source variant with each node in the role of the root node. In pseudocode such an implementation could look as follows: 1 func DijkstraSSSP(''G'',''v'') 5 6 func DijkstraAPSP(''G'') In this example we assume thatDijkstraSSSP takes the graph and the root node as input.
The result of the execution in turn is the distancelist . In , the -th element stores the distance from the root node to the node .
Therefore the list corresponds exactly to the -th row of the APSP distancematrix .
For this reason, DijkstraAPSP iterates over all nodes of the graph and executes DijkstraSSSP with each as root node while storing the results in .
The runtime of DijkstraSSSP is as we expect the graph to be represented using an adjacency matrix
In graph theory and computer science, an adjacency matrix is a square matrix used to represent a finite graph. The elements of the matrix indicate whether pairs of vertices are adjacent or not in the graph.
In the special case of a finite simple ...
.
Therefore DijkstraAPSP has a total sequential runtime of .
Parallelization for up to , ''V'', processors
A trivial parallelization can be obtained by parallelizing the loop ofDijkstraAPSP in line''8''.
However, when using the sequential DijkstraSSSP this limits the number of processors to be used by the number of iterations executed in the loop.
Therefore, for this trivial parallelization is an upper bound for the number of processors.
For example, let the number of processors be equal to the number of nodes . This results in each processor executing DijkstraSSSP exactly once in parallel.
However, when there are only for example processors available, each processor has to execute DijkstraSSSP twice.
In total this yields a runtime of , when is a multiple of .
Consequently, the efficiency of this parallelization is perfect: Employing processors reduces the runtime by the factor .
Another benefit of this parallelization is that no communication between the processors is required. However, it is required that every processor has enough local memory to store the entire adjacency matrix of the graph.
Parallelization for more than , ''V'', processors

 If more than processors shall be used for the parallelization, it is required that multiple processors take part of the
If more than processors shall be used for the parallelization, it is required that multiple processors take part of the DijkstraSSSP computation. For this reason, the parallelization is split across into two levels.
For the first level the processors are split into partitions.
Each partition is responsible for the computation of a single row of the distancematrix . This means each partition has to evaluate one DijkstraSSSP execution with a fixed root node.
With this definition each partition has a size of processors. The partitions can perform their computations in parallel as the results of each are independent of each other. Therefore, the parallelization presented in the previous section corresponds to a partition size of 1 with processors.
The main difficulty is the parallelization of multiple processors executing DijkstraSSSP for a single root node. The idea for this parallelization is to distribute the management of the distancelist in DijkstraSSSP within the partition. Each processor in the partition therefore is exclusively responsible for elements of . For example, consider and : this yields a partition size of . In this case, the first processor of each partition is responsible for , and the second processor is responsible for and . Hereby, the total distance lists is