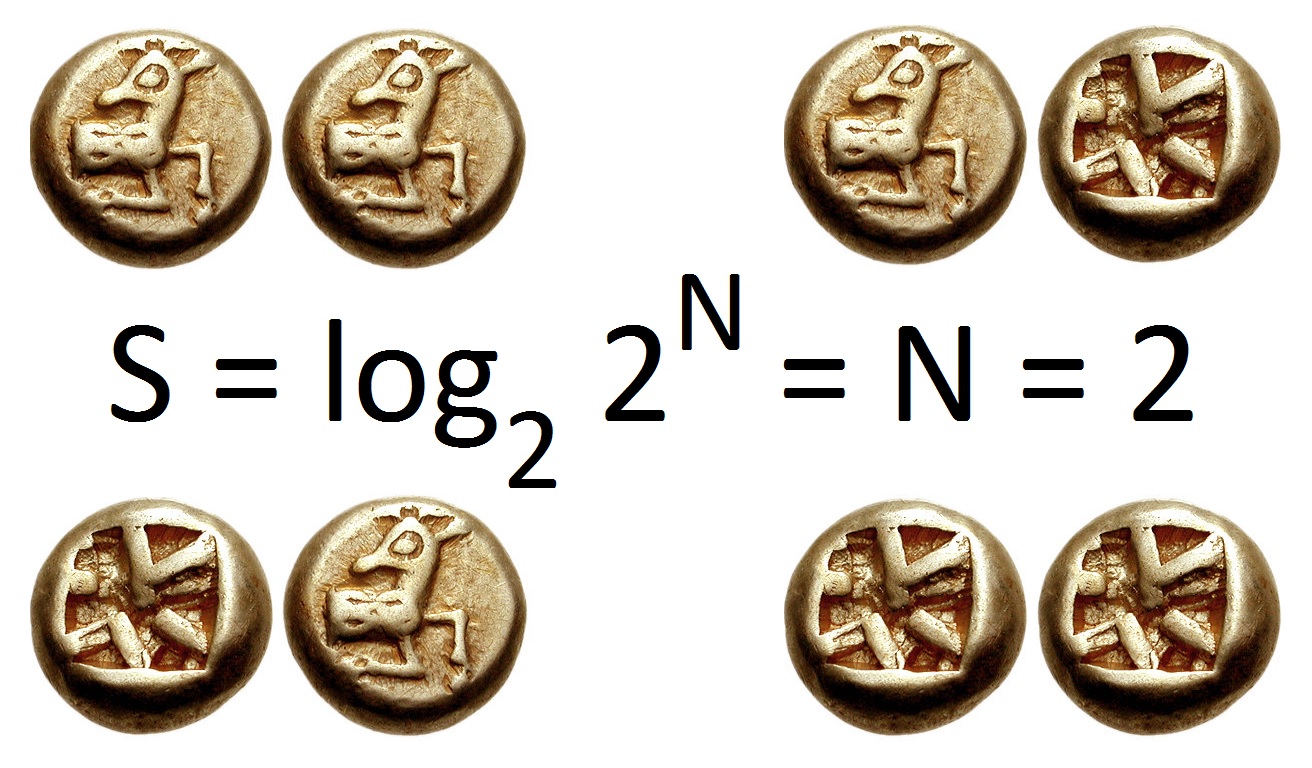|
Optimal Design
In the design of experiments, optimal experimental designs (or optimum designs) are a class of experimental designs that are optimal with respect to some statistical criterion. The creation of this field of statistics has been credited to Danish statistician Kirstine Smith. In the design of experiments for estimating statistical models, optimal designs allow parameters to be estimated without bias and with minimum variance. A non-optimal design requires a greater number of experimental runs to estimate the parameters with the same precision as an optimal design. In practical terms, optimal experiments can reduce the costs of experimentation. The optimality of a design depends on the statistical model and is assessed with respect to a statistical criterion, which is related to the variance-matrix of the estimator. Specifying an appropriate model and specifying a suitable criterion function both require understanding of statistical theory and practical knowledge with ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Design Of Experiments
The design of experiments (DOE), also known as experiment design or experimental design, is the design of any task that aims to describe and explain the variation of information under conditions that are hypothesized to reflect the variation. The term is generally associated with experiments in which the design introduces conditions that directly affect the variation, but may also refer to the design of quasi-experiments, in which natural conditions that influence the variation are selected for observation. In its simplest form, an experiment aims at predicting the outcome by introducing a change of the preconditions, which is represented by one or more independent variables, also referred to as "input variables" or "predictor variables." The change in one or more independent variables is generally hypothesized to result in a change in one or more dependent variables, also referred to as "output variables" or "response variables." The experimental design may also identify ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bias Of An Estimator
In statistics, the bias of an estimator (or bias function) is the difference between this estimator's expected value and the true value of the parameter being estimated. An estimator or decision rule with zero bias is called ''unbiased''. In statistics, "bias" is an property of an estimator. Bias is a distinct concept from consistency: consistent estimators converge in probability to the true value of the parameter, but may be biased or unbiased (see bias versus consistency for more). All else being equal, an unbiased estimator is preferable to a biased estimator, although in practice, biased estimators (with generally small bias) are frequently used. When a biased estimator is used, bounds of the bias are calculated. A biased estimator may be used for various reasons: because an unbiased estimator does not exist without further assumptions about a population; because an estimator is difficult to compute (as in unbiased estimation of standard deviation); because a biased esti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matrix (mathematics)
In mathematics, a matrix (: matrices) is a rectangle, rectangular array or table of numbers, symbol (formal), symbols, or expression (mathematics), expressions, with elements or entries arranged in rows and columns, which is used to represent a mathematical object or property of such an object. For example, \begin1 & 9 & -13 \\20 & 5 & -6 \end is a matrix with two rows and three columns. This is often referred to as a "two-by-three matrix", a " matrix", or a matrix of dimension . Matrices are commonly used in linear algebra, where they represent linear maps. In geometry, matrices are widely used for specifying and representing geometric transformations (for example rotation (mathematics), rotations) and coordinate changes. In numerical analysis, many computational problems are solved by reducing them to a matrix computation, and this often involves computing with matrices of huge dimensions. Matrices are used in most areas of mathematics and scientific fields, either directly ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Covariance Matrix
In probability theory and statistics, a covariance matrix (also known as auto-covariance matrix, dispersion matrix, variance matrix, or variance–covariance matrix) is a square matrix giving the covariance between each pair of elements of a given random vector. Intuitively, the covariance matrix generalizes the notion of variance to multiple dimensions. As an example, the variation in a collection of random points in two-dimensional space cannot be characterized fully by a single number, nor would the variances in the x and y directions contain all of the necessary information; a 2 \times 2 matrix would be necessary to fully characterize the two-dimensional variation. Any covariance matrix is symmetric and positive semi-definite and its main diagonal contains variances (i.e., the covariance of each element with itself). The covariance matrix of a random vector \mathbf is typically denoted by \operatorname_, \Sigma or S. Definition Throughout this article, boldfaced u ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coordinate Vector
In linear algebra, a coordinate vector is a representation of a vector as an ordered list of numbers (a tuple) that describes the vector in terms of a particular ordered basis. An easy example may be a position such as (5, 2, 1) in a 3-dimensional Cartesian coordinate system with the basis as the axes of this system. Coordinates are always specified relative to an ordered basis. Bases and their associated coordinate representations let one realize vector spaces and linear transformations concretely as column vectors, row vectors, and matrices; hence, they are useful in calculations. The idea of a coordinate vector can also be used for infinite-dimensional vector spaces, as addressed below. Definition Let ''V'' be a vector space of dimension ''n'' over a field ''F'' and let : B = \ be an ordered basis for ''V''. Then for every v \in V there is a unique linear combination of the basis vectors that equals '' v '': : v = \alpha _1 b_1 + \alpha _2 b_2 + \cdots + \alpha _n b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Functional (mathematics)
In mathematics, a functional is a certain type of function. The exact definition of the term varies depending on the subfield (and sometimes even the author). * In linear algebra, it is synonymous with a linear form, which is a linear mapping from a vector space V into its field of scalars (that is, it is an element of the dual space V^*) "Let ''E'' be a free module over a commutative ring ''A''. We view ''A'' as a free module of rank 1 over itself. By the dual module ''E''∨ of ''E'' we shall mean the module Hom(''E'', ''A''). Its elements will be called functionals. Thus a functional on ''E'' is an ''A''-linear map ''f'' : ''E'' → ''A''." * In functional analysis and related fields, it refers to a mapping from a space X into the field of real or complex numbers. "A numerical function ''f''(''x'') defined on a normed linear space ''R'' will be called a ''functional''. A functional ''f''(''x'') is said to be ''linear'' if ''f''(α''x'' + β''y'') = α''f''(''x'') + β ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Entropy (information Theory)
In information theory, the entropy of a random variable quantifies the average level of uncertainty or information associated with the variable's potential states or possible outcomes. This measures the expected amount of information needed to describe the state of the variable, considering the distribution of probabilities across all potential states. Given a discrete random variable X, which may be any member x within the set \mathcal and is distributed according to p\colon \mathcal\to[0, 1], the entropy is \Eta(X) := -\sum_ p(x) \log p(x), where \Sigma denotes the sum over the variable's possible values. The choice of base for \log, the logarithm, varies for different applications. Base 2 gives the unit of bits (or "shannon (unit), shannons"), while base Euler's number, ''e'' gives "natural units" nat (unit), nat, and base 10 gives units of "dits", "bans", or "Hartley (unit), hartleys". An equivalent definition of entropy is the expected value of the self-information of a v ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fisher Information
In mathematical statistics, the Fisher information is a way of measuring the amount of information that an observable random variable ''X'' carries about an unknown parameter ''θ'' of a distribution that models ''X''. Formally, it is the variance of the score, or the expected value of the observed information. The role of the Fisher information in the asymptotic theory of maximum-likelihood estimation was emphasized and explored by the statistician Sir Ronald Fisher (following some initial results by Francis Ysidro Edgeworth). The Fisher information matrix is used to calculate the covariance matrices associated with maximum-likelihood estimates. It can also be used in the formulation of test statistics, such as the Wald test. In Bayesian statistics, the Fisher information plays a role in the derivation of non-informative prior distributions according to Jeffreys' rule. It also appears as the large-sample covariance of the posterior distribution, provided that the prior i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Efficiency
In statistics, efficiency is a measure of quality of an estimator, of an experimental design, or of a hypothesis testing procedure. Essentially, a more efficient estimator needs fewer input data or observations than a less efficient one to achieve the Cramér–Rao bound. An ''efficient estimator'' is characterized by having the smallest possible variance, indicating that there is a small deviance between the estimated value and the "true" value in the L2 norm sense. The relative efficiency of two procedures is the ratio of their efficiencies, although often this concept is used where the comparison is made between a given procedure and a notional "best possible" procedure. The efficiencies and the relative efficiency of two procedures theoretically depend on the sample size available for the given procedure, but it is often possible to use the asymptotic relative efficiency (defined as the limit of the relative efficiencies as the sample size grows) as the principal comparison ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reciprocal (mathematics)
In mathematics, a multiplicative inverse or reciprocal for a number ''x'', denoted by 1/''x'' or ''x''−1, is a number which when multiplied by ''x'' yields the multiplicative identity, 1. The multiplicative inverse of a fraction ''a''/''b'' is ''b''/''a''. For the multiplicative inverse of a real number, divide 1 by the number. For example, the reciprocal of 5 is one fifth (1/5 or 0.2), and the reciprocal of 0.25 is 1 divided by 0.25, or 4. The reciprocal function, the function ''f''(''x'') that maps ''x'' to 1/''x'', is one of the simplest examples of a function which is its own inverse (an involution). Multiplying by a number is the same as dividing by its reciprocal and vice versa. For example, multiplication by 4/5 (or 0.8) will give the same result as division by 5/4 (or 1.25). Therefore, multiplication by a number followed by multiplication by its reciprocal yields the original number (since the product of the number and its reciprocal is 1). The term ''reciproca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parameter
A parameter (), generally, is any characteristic that can help in defining or classifying a particular system (meaning an event, project, object, situation, etc.). That is, a parameter is an element of a system that is useful, or critical, when identifying the system, or when evaluating its performance, status, condition, etc. ''Parameter'' has more specific meanings within various disciplines, including mathematics, computer programming, engineering, statistics, logic, linguistics, and electronic musical composition. In addition to its technical uses, there are also extended uses, especially in non-scientific contexts, where it is used to mean defining characteristics or boundaries, as in the phrases 'test parameters' or 'game play parameters'. Modelization When a system theory, system is modeled by equations, the values that describe the system are called ''parameters''. For example, in mechanics, the masses, the dimensions and shapes (for solid bodies), the densities and t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Real Number
In mathematics, a real number is a number that can be used to measure a continuous one- dimensional quantity such as a duration or temperature. Here, ''continuous'' means that pairs of values can have arbitrarily small differences. Every real number can be almost uniquely represented by an infinite decimal expansion. The real numbers are fundamental in calculus (and in many other branches of mathematics), in particular by their role in the classical definitions of limits, continuity and derivatives. The set of real numbers, sometimes called "the reals", is traditionally denoted by a bold , often using blackboard bold, . The adjective ''real'', used in the 17th century by René Descartes, distinguishes real numbers from imaginary numbers such as the square roots of . The real numbers include the rational numbers, such as the integer and the fraction . The rest of the real numbers are called irrational numbers. Some irrational numbers (as well as all the rationals) a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |