|
Mary Rees
Susan Mary Rees (born 31 July 1953) is a British mathematician and an emeritus professor of mathematics at the University of Liverpool since 2018, specialising in research in complex dynamical systems. Career Rees was born in Cambridge. After obtaining her BA in 1974 and MSc in 1975 at St Hugh's College, Oxford, she did research in mathematics under the direction of Bill Parry at the University of Warwick, obtaining a PhD in 1978. Her first postdoctoral position was at the Institute for Advanced Study from 1978 to 1979. Later she worked at Institut des hautes études scientifiques and the University of Minnesota. Following this she worked at the University of Liverpool until her retirement. She became professor of mathematics in 2002 and retired in 2018, becoming an emeritus professor. She was awarded a Whitehead Prize of the London Mathematical Society in 1988. The citation notes that, in particular, Her most spectacular theorem has been to show that in the space of ration ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematician
A mathematician is someone who uses an extensive knowledge of mathematics in their work, typically to solve mathematical problems. Mathematicians are concerned with numbers, data, quantity, mathematical structure, structure, space, Mathematical model, models, and mathematics#Calculus and analysis, change. History One of the earliest known mathematicians was Thales of Miletus (); he has been hailed as the first true mathematician and the first known individual to whom a mathematical discovery has been attributed. He is credited with the first use of deductive reasoning applied to geometry, by deriving four corollaries to Thales's theorem. The number of known mathematicians grew when Pythagoras of Samos () established the Pythagorean school, whose doctrine it was that mathematics ruled the universe and whose motto was "All is number". It was the Pythagoreans who coined the term "mathematics", and with whom the study of mathematics for its own sake begins. The first woman math ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Absolutely Continuous
In calculus and real analysis, absolute continuity is a smoothness property of functions that is stronger than continuity and uniform continuity. The notion of absolute continuity allows one to obtain generalizations of the relationship between the two central operations of calculus— differentiation and integration. This relationship is commonly characterized (by the fundamental theorem of calculus) in the framework of Riemann integration, but with absolute continuity it may be formulated in terms of Lebesgue integration. For real-valued functions on the real line, two interrelated notions appear: absolute continuity of functions and absolute continuity of measures. These two notions are generalized in different directions. The usual derivative of a function is related to the '' Radon–Nikodym derivative'', or ''density'', of a measure. We have the following chains of inclusions for functions over a compact subset of the real line: : ''absolutely continuous'' ⊆ '' u ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
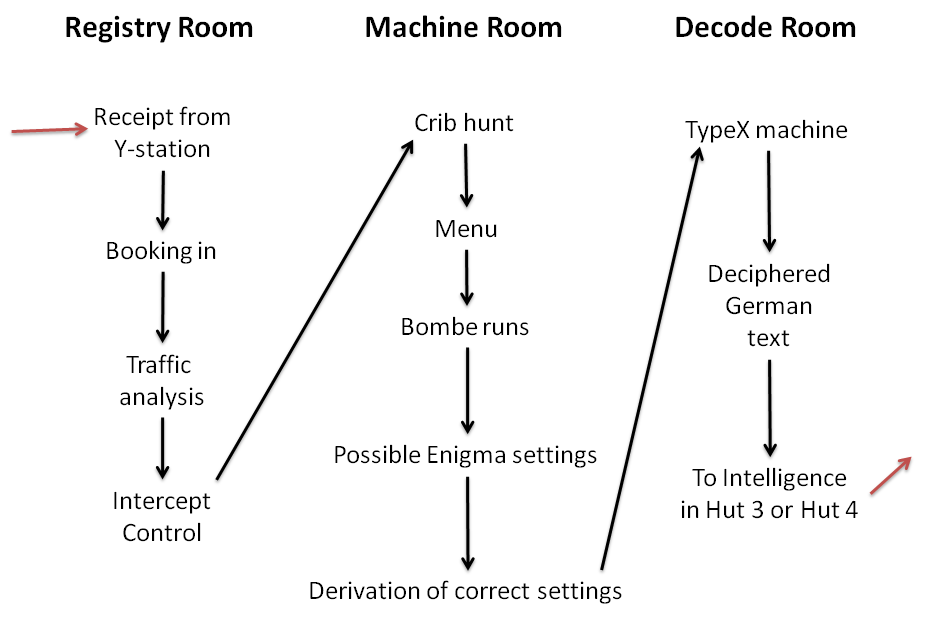
Bletchley Park
Bletchley Park is an English country house and Bletchley Park estate, estate in Bletchley, Milton Keynes (Buckinghamshire), that became the principal centre of Allies of World War II, Allied World War II cryptography, code-breaking during the Second World War. During World War II, the estate housed the Government Code and Cypher School (GC&CS), which regularly penetrated the secret communications of the Axis Powers most importantly the German Enigma machine, Enigma and Lorenz cipher, Lorenz ciphers. The GC&CS team of codebreakers included John Tiltman, Dilwyn Knox, Alan Turing, Harry Golombek, Gordon Welchman, Conel Hugh O'Donel Alexander, Hugh Alexander, Donald Michie, W. T. Tutte, Bill Tutte and Stuart Milner-Barry. The team at Bletchley Park devised automatic machinery to help with decryption, culminating in the development of Colossus computer, Colossus, the world's first programmable digital electronic computer. Codebreaking operations at Bletchley Park ended in 1946 and al ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hut 6
Hut 6 was a wartime section of the Government Code and Cypher School at Bletchley Park, Buckinghamshire, Britain, tasked with the solution of German Army and Air Force Enigma machine cyphers. Hut 8, by contrast, attacked Naval Enigma. Hut 6 was established at the initiative of Gordon Welchman, and was run initially by Welchman and fellow Cambridge mathematician John Jeffreys. Welchman's deputy, Stuart Milner-Barry, succeeded Welchman as head of Hut 6 in September 1943, at which point over 450 people were working in the section.Ralph Erskine, ''Barry, Sir (Philip) Stuart Milner- (1906–1995)'', Oxford Dictionary of National Biography, 2004. Hut 6 was partnered with Hut 3, which handled the translation and intelligence analysis of the raw decrypts provided by Hut 6. Location Hut 6 was originally named after the building in which the section was located. Welchman says the hut was 20 yards (18m) long by 10 yards (9m) wide, with two large rooms at the far end – and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Enigma Machine
The Enigma machine is a cipher device developed and used in the early- to mid-20th century to protect commercial, diplomatic, and military communication. It was employed extensively by Nazi Germany during World War II, in all branches of the Wehrmacht, German military. The Enigma machine was considered so secure that it was used to encipher the most top-secret messages. The Enigma has an electromechanical Rotor machine, rotor mechanism that scrambles the 26 letters of the alphabet. In typical use, one person enters text on the Enigma's keyboard and another person writes down which of the 26 lights above the keyboard illuminated at each key press. If plaintext is entered, the illuminated letters are the ciphertext. Entering ciphertext transforms it back into readable plaintext. The rotor mechanism changes the electrical connections between the keys and the lights with each keypress. The security of the system depends on machine settings that were generally changed daily, based ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
David Rees (mathematician)
David Rees FRS (29 May 1918 – 16 August 2013) was a British professor of pure mathematics at the University of Exeter, having been head of the Mathematics / Mathematical Sciences Department at Exeter from 1958 to 1983. During the Second World War, Rees was active on Enigma research in Hut 6 at Bletchley Park. Early life Rees was born in Abergavenny to David Rees (1881–), a corn merchant, and his wife Florence Gertrude (Gertie) née Powell (1884–1970), the 4th out of 5 children. Despite periods of ill health and absence, he successfully completed his early education at King Henry VIII Grammar School. Education and career Rees won a scholarship to Sidney Sussex College, Cambridge, supervised by Gordon Welchman and graduating in summer 1939. On completion of his education, he initially worked on semigroup theory; the Rees factor semigroup is named after him. He also characterised completely simple and completely 0-simple semigroups, in what is nowadays known as Rees ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Royal Society
The Royal Society, formally The Royal Society of London for Improving Natural Knowledge, is a learned society and the United Kingdom's national academy of sciences. The society fulfils a number of roles: promoting science and its benefits, recognising excellence in science, supporting outstanding science, providing scientific advice for policy, education and public engagement and fostering international and global co-operation. Founded on 28 November 1660, it was granted a royal charter by Charles II of England, King Charles II and is the oldest continuously existing scientific academy in the world. The society is governed by its Council, which is chaired by the society's president, according to a set of statutes and standing orders. The members of Council and the president are elected from and by its Fellows, the basic members of the society, who are themselves elected by existing Fellows. , there are about 1,700 fellows, allowed to use the postnominal title FRS (Fellow ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Yair Minsky
Yair Nathan Minsky (born in 1962) is an Israeli- American mathematician whose research concerns three-dimensional topology, differential geometry, group theory and holomorphic dynamics. He is a professor at Yale University. He is known for having proved Thurston's ending lamination conjecture and as a student of curve complex geometry. Biography Minsky obtained his Ph.D. from Princeton University in 1989 under the supervision of William Paul Thurston, with the thesis ''Harmonic Maps and Hyperbolic Geometry''. His Ph.D. students include Jason Behrstock, Erica Klarreich, Hossein Namazi and Kasra Rafi. Honors and awards He received a Sloan Fellowship in 1995. He was a speaker at the ICM (Madrid) 2006. He was named to the 2021 class of fellows of the American Mathematical Society "for contributions to hyperbolic 3-manifolds, low-dimensional topology, geometric group theory and Teichmuller theory". He was elected to the American Academy of Arts and Sciences in 2023. Sele ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Richard Canary
Richard Douglas Canary (born in 1962) is an American mathematician working mainly on low-dimensional topology. He is a professor at the University of Michigan. Canary obtained his Ph.D. from Princeton University in 1989 under the supervision of William Paul Thurston, with the thesis ''Hyperbolic Structures on 3-Manifolds with Compressible Boundaries''. He received a Sloan Research Fellowship in 1993. In 2015 he became a fellow of the American Mathematical Society, "for contributions to low-dimensional topology and hyperbolic geometry In mathematics, hyperbolic geometry (also called Lobachevskian geometry or János Bolyai, Bolyai–Nikolai Lobachevsky, Lobachevskian geometry) is a non-Euclidean geometry. The parallel postulate of Euclidean geometry is replaced with: :For a ... as well as for service and teaching in mathematics." References External links Canary's home page at the University of Michigan [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
William Thurston
William Paul Thurston (October 30, 1946August 21, 2012) was an American mathematician. He was a pioneer in the field of low-dimensional topology and was awarded the Fields Medal in 1982 for his contributions to the study of 3-manifolds. Thurston was a professor of mathematics at Princeton University, University of California, Davis, and Cornell University. He was also a director of the Mathematical Sciences Research Institute. Early life and education William Thurston was born in Washington, D.C., to Margaret Thurston (), a seamstress, and Paul Thurston, an aeronautical engineer. William Thurston suffered from congenital strabismus as a child, causing issues with depth perception. His mother worked with him as a toddler to reconstruct three-dimensional images from two-dimensional ones. He received his bachelor's degree from New College in 1967 as part of its inaugural class. For his undergraduate thesis, he developed an intuitionist foundation for topology. Following th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ending Lamination Theorem
In hyperbolic geometry, the ending lamination theorem, originally conjectured by as the eleventh problem out of his twenty-four questions, states that hyperbolic 3-manifolds with finitely generated fundamental groups are determined by their topology together with certain "end invariants", which are geodesic laminations on some surfaces in the boundary of the manifold. The ending lamination theorem is a generalization of the Mostow rigidity theorem to hyperbolic manifolds of infinite volume. When the manifold is compact or of finite volume, the Mostow rigidity theorem states that the fundamental group determines the manifold. When the volume is infinite the fundamental group is not enough to determine the manifold: one also needs to know the hyperbolic structure on the surfaces at the "ends" of the manifold, and also the ending laminations on these surfaces. and proved the ending lamination conjecture for Kleinian surface groups. In view of the Tameness theorem this implies ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |