 |
Manifold Regularization
In machine learning, Manifold regularization is a technique for using the shape of a dataset to constrain the functions that should be learned on that dataset. In many machine learning problems, the data to be learned do not cover the entire input space. For example, a facial recognition system may not need to classify any possible image, but only the subset of images that contain faces. The technique of manifold learning assumes that the relevant subset of data comes from a manifold, a mathematical structure with useful properties. The technique also assumes that the function to be learned is ''smooth'': data with different labels are not likely to be close together, and so the labeling function should not change quickly in areas where there are likely to be many data points. Because of this assumption, a manifold regularization algorithm can use unlabeled data to inform where the learned function is allowed to change quickly and where it is not, using an extension of the techniqu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Semi-supervised Learning
Weak supervision (also known as semi-supervised learning) is a paradigm in machine learning, the relevance and notability of which increased with the advent of large language models due to large amount of data required to train them. It is characterized by using a combination of a small amount of human-labeled data (exclusively used in more expensive and time-consuming supervised learning paradigm), followed by a large amount of unlabeled data (used exclusively in unsupervised learning paradigm). In other words, the desired output values are provided only for a subset of the training data. The remaining data is unlabeled or imprecisely labeled. Intuitively, it can be seen as an exam and labeled data as sample problems that the teacher solves for the class as an aid in solving another set of problems. In the Transduction (machine learning), transductive setting, these unsolved problems act as exam questions. In the Inductive reasoning, inductive setting, they become practice problems ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
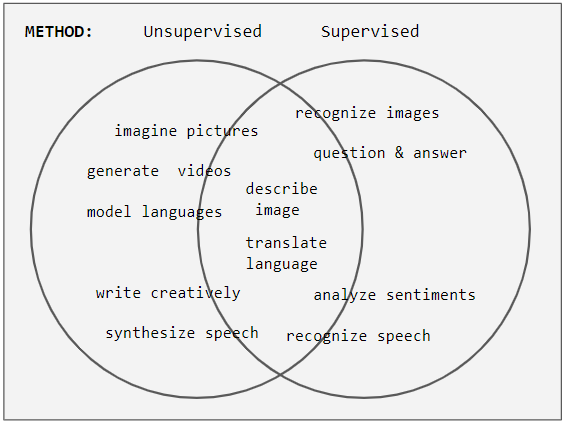
Example Of Unlabeled Data In Semisupervised Learning
Example may refer to: * ''exempli gratia'' (e.g.), usually read out in English as "for example" * .example, reserved as a domain name that may not be installed as a top-level domain of the Internet ** example.com, example.net, example.org, and example.edu: second-level domain names reserved for use in documentation as examples * HMS ''Example'' (P165), an Archer-class patrol and training vessel of the Royal Navy Arts * ''The Example'', a 1634 play by James Shirley * ''The Example'' (comics), a 2009 graphic novel by Tom Taylor and Colin Wilson * Example (musician), the British dance musician Elliot John Gleave (born 1982) * ''Example'' (album), a 1995 album by American rock band For Squirrels See also * Exemplar (other), a prototype or model which others can use to understand a topic better * Exemplum, medieval collections of short stories to be told in sermons * Eixample The Eixample (, ) is a district of Barcelona between the old city (Ciutat Vella) a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Manifold Hypothesis
The manifold hypothesis posits that many high-dimensional data sets that occur in the real world actually lie along low-dimensional latent manifolds inside that high-dimensional space. As a consequence of the manifold hypothesis, many data sets that appear to initially require many variables to describe, can actually be described by a comparatively small number of variables, likened to the local coordinate system of the underlying manifold. It is suggested that this principle underpins the effectiveness of machine learning algorithms in describing high-dimensional data sets by considering a few common features. The manifold hypothesis is related to the effectiveness of nonlinear dimensionality reduction techniques in machine learning. Many techniques of dimensional reduction make the assumption that data lies along a low-dimensional submanifold, such as manifold sculpting, manifold alignment, and manifold regularization. The major implications of this hypothesis is that * Mac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Least Squares
The method of least squares is a mathematical optimization technique that aims to determine the best fit function by minimizing the sum of the squares of the differences between the observed values and the predicted values of the model. The method is widely used in areas such as regression analysis, curve fitting and data modeling. The least squares method can be categorized into linear and nonlinear forms, depending on the relationship between the model parameters and the observed data. The method was first proposed by Adrien-Marie Legendre in 1805 and further developed by Carl Friedrich Gauss. History Founding The method of least squares grew out of the fields of astronomy and geodesy, as scientists and mathematicians sought to provide solutions to the challenges of navigating the Earth's oceans during the Age of Discovery. The accurate description of the behavior of celestial bodies was the key to enabling ships to sail in open seas, where sailors could no longer rely on la ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Support Vector Machines
In machine learning, support vector machines (SVMs, also support vector networks) are supervised max-margin models with associated learning algorithms that analyze data for classification and regression analysis. Developed at AT&T Bell Laboratories, SVMs are one of the most studied models, being based on statistical learning frameworks of VC theory proposed by Vapnik (1982, 1995) and Chervonenkis (1974). In addition to performing linear classification, SVMs can efficiently perform non-linear classification using the ''kernel trick'', representing the data only through a set of pairwise similarity comparisons between the original data points using a kernel function, which transforms them into coordinates in a higher-dimensional feature space. Thus, SVMs use the kernel trick to implicitly map their inputs into high-dimensional feature spaces, where linear classification can be performed. Being max-margin models, SVMs are resilient to noisy data (e.g., misclassified examples). ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Finite Difference Method
In numerical analysis, finite-difference methods (FDM) are a class of numerical techniques for solving differential equations by approximating Derivative, derivatives with Finite difference approximation, finite differences. Both the spatial domain and time domain (if applicable) are Discretization, discretized, or broken into a finite number of intervals, and the values of the solution at the end points of the intervals are approximated by solving algebraic equations containing finite differences and values from nearby points. Finite difference methods convert ordinary differential equations (ODE) or partial differential equations (PDE), which may be Nonlinear partial differential equation, nonlinear, into a system of linear equations that can be solved by matrix algebra techniques. Modern computers can perform these linear algebra computations efficiently, and this, along with their relative ease of implementation, has led to the widespread use of FDM in modern numerical analysi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Meshfree Methods
In the field of numerical analysis, meshfree methods are those that do not require connection between nodes of the simulation domain, i.e. a mesh, but are rather based on interaction of each node with all its neighbors. As a consequence, original extensive properties such as mass or kinetic energy are no longer assigned to mesh elements but rather to the single nodes. Meshfree methods enable the simulation of some otherwise difficult types of problems, at the cost of extra computing time and programming effort. The absence of a mesh allows Lagrangian simulations, in which the nodes can move according to the velocity field. Motivation Numerical methods such as the finite difference method, finite-volume method, and finite element method were originally defined on meshes of data points. In such a mesh, each point has a fixed number of predefined neighbors, and this connectivity between neighbors can be used to define mathematical operators like the derivative. These operators ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Curse Of Dimensionality
The curse of dimensionality refers to various phenomena that arise when analyzing and organizing data in high-dimensional spaces that do not occur in low-dimensional settings such as the three-dimensional physical space of everyday experience. The expression was coined by Richard E. Bellman when considering problems in dynamic programming. The curse generally refers to issues that arise when the number of datapoints is small (in a suitably defined sense) relative to the intrinsic dimension of the data. Dimensionally cursed phenomena occur in domains such as numerical analysis, sampling, combinatorics, machine learning, data mining and databases. The common theme of these problems is that when the dimensionality increases, the volume of the space increases so fast that the available data become sparse. In order to obtain a reliable result, the amount of data needed often grows exponentially with the dimensionality. Also, organizing and searching data often relies on detecting a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
K-nearest Neighbors Algorithm
In statistics, the ''k''-nearest neighbors algorithm (''k''-NN) is a Non-parametric statistics, non-parametric supervised learning method. It was first developed by Evelyn Fix and Joseph Lawson Hodges Jr., Joseph Hodges in 1951, and later expanded by Thomas M. Cover, Thomas Cover. Most often, it is used for statistical classification, classification, as a ''k''-NN classifier, the output of which is a class membership. An object is classified by a plurality vote of its neighbors, with the object being assigned to the class most common among its ''k'' nearest neighbors (''k'' is a positive integer, typically small). If ''k'' = 1, then the object is simply assigned to the class of that single nearest neighbor. The ''k''-NN algorithm can also be generalized for regression analysis, regression. In ''-NN regression'', also known as ''nearest neighbor smoothing'', the output is the property value for the object. This value is the average of the values of ''k'' nearest neighbo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Representer Theorem
For computer science, in statistical learning theory, a representer theorem is any of several related results stating that a minimizer f^ of a regularized Empirical risk minimization, empirical risk functional defined over a reproducing kernel Hilbert space can be represented as a finite linear combination of kernel products evaluated on the input points in the training set data. Formal statement The following Representer Theorem and its proof are due to Bernhard Schölkopf, Schölkopf, Herbrich, and Smola: Theorem: Consider a positive-definite real-valued kernel k : \mathcal \times \mathcal \to \R on a non-empty set \mathcal with a corresponding reproducing kernel Hilbert space H_k. Let there be given * a training sample (x_1, y_1), \dotsc, (x_n, y_n) \in \mathcal \times \R, * a strictly increasing real-valued function g \colon [0, \infty) \to \R, and * an arbitrary error function E \colon (\mathcal \times \R^2)^n \to \R \cup \lbrace \infty \rbrace, which together define the f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Kernel Methods
In machine learning, kernel machines are a class of algorithms for pattern analysis, whose best known member is the support-vector machine (SVM). These methods involve using linear classifiers to solve nonlinear problems. The general task of pattern analysis is to find and study general types of relations (for example clusters, rankings, principal components, correlations, classifications) in datasets. For many algorithms that solve these tasks, the data in raw representation have to be explicitly transformed into feature vector representations via a user-specified ''feature map'': in contrast, kernel methods require only a user-specified ''kernel'', i.e., a similarity function over all pairs of data points computed using inner products. The feature map in kernel machines is infinite dimensional but only requires a finite dimensional matrix from user-input according to the representer theorem. Kernel machines are slow to compute for datasets larger than a couple of thousa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Divergence
In vector calculus, divergence is a vector operator that operates on a vector field, producing a scalar field giving the rate that the vector field alters the volume in an infinitesimal neighborhood of each point. (In 2D this "volume" refers to area.) More precisely, the divergence at a point is the rate that the flow of the vector field modifies a volume about the point ''in the limit'', as a small volume shrinks down to the point. As an example, consider air as it is heated or cooled. The velocity of the air at each point defines a vector field. While air is heated in a region, it expands in all directions, and thus the velocity field points outward from that region. The divergence of the velocity field in that region would thus have a positive value. While the air is cooled and thus contracting, the divergence of the velocity has a negative value. Physical interpretation of divergence In physical terms, the divergence of a vector field is the extent to which the vector fi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |