|
Curse Of Dimensionality
The curse of dimensionality refers to various phenomena that arise when analyzing and organizing data in high-dimensional spaces that do not occur in low-dimensional settings such as the three-dimensional physical space of everyday experience. The expression was coined by Richard E. Bellman when considering problems in dynamic programming. The curse generally refers to issues that arise when the number of datapoints is small (in a suitably defined sense) relative to the intrinsic dimension of the data. Dimensionally cursed phenomena occur in domains such as numerical analysis, sampling, combinatorics, machine learning, data mining and databases. The common theme of these problems is that when the dimensionality increases, the volume of the space increases so fast that the available data become sparse. In order to obtain a reliable result, the amount of data needed often grows exponentially with the dimensionality. Also, organizing and searching data often relies on detecting a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
High-dimensional Space
In physics and mathematics, the dimension of a mathematical space (or object) is informally defined as the minimum number of coordinates needed to specify any point within it. Thus, a line has a dimension of one (1D) because only one coordinate is needed to specify a point on itfor example, the point at 5 on a number line. A surface, such as the boundary of a cylinder or sphere, has a dimension of two (2D) because two coordinates are needed to specify a point on itfor example, both a latitude and longitude are required to locate a point on the surface of a sphere. A two-dimensional Euclidean space is a two-dimensional space on the plane. The inside of a cube, a cylinder or a sphere is three-dimensional (3D) because three coordinates are needed to locate a point within these spaces. In classical mechanics, space and time are different categories and refer to absolute space and time. That conception of the world is a four-dimensional space but not the one that was found nec ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Optimization (mathematics)
Mathematical optimization (alternatively spelled ''optimisation'') or mathematical programming is the selection of a best element, with regard to some criteria, from some set of available alternatives. It is generally divided into two subfields: discrete optimization and continuous optimization. Optimization problems arise in all quantitative disciplines from computer science and engineering to operations research and economics, and the development of solution methods has been of interest in mathematics for centuries. In the more general approach, an optimization problem consists of maxima and minima, maximizing or minimizing a Function of a real variable, real function by systematically choosing Argument of a function, input values from within an allowed set and computing the Value (mathematics), value of the function. The generalization of optimization theory and techniques to other formulations constitutes a large area of applied mathematics. Optimization problems Opti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Distance
In mathematics, the Euclidean distance between two points in Euclidean space is the length of the line segment between them. It can be calculated from the Cartesian coordinates of the points using the Pythagorean theorem, and therefore is occasionally called the Pythagorean distance. These names come from the ancient Greek mathematicians Euclid and Pythagoras. In the Greek deductive geometry exemplified by Euclid's ''Elements'', distances were not represented as numbers but line segments of the same length, which were considered "equal". The notion of distance is inherent in the compass tool used to draw a circle, whose points all have the same distance from a common center point. The connection from the Pythagorean theorem to distance calculation was not made until the 18th century. The distance between two objects that are not points is usually defined to be the smallest distance among pairs of points from the two objects. Formulas are known for computing distances b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Interquartile Range
In descriptive statistics, the interquartile range (IQR) is a measure of statistical dispersion, which is the spread of the data. The IQR may also be called the midspread, middle 50%, fourth spread, or H‑spread. It is defined as the difference between the 75th and 25th percentiles of the data. To calculate the IQR, the data set is divided into quartiles, or four rank-ordered even parts via linear interpolation. These quartiles are denoted by ''Q''1 (also called the lower quartile), ''Q''2 (the median), and ''Q''3 (also called the upper quartile). The lower quartile corresponds with the 25th percentile and the upper quartile corresponds with the 75th percentile, so IQR = ''Q''3 − ''Q''1. The IQR is an example of a trimmed estimator, defined as the 25% trimmed range, which enhances the accuracy of dataset statistics by dropping lower contribution, outlying points. It is also used as a robust measure of scale It can be clearly visualized by the box on a box plot. Use ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dimensionality Reduction
Dimensionality reduction, or dimension reduction, is the transformation of data from a high-dimensional space into a low-dimensional space so that the low-dimensional representation retains some meaningful properties of the original data, ideally close to its intrinsic dimension. Working in high-dimensional spaces can be undesirable for many reasons; raw data are often sparse as a consequence of the curse of dimensionality, and analyzing the data is usually computationally intractable. Dimensionality reduction is common in fields that deal with large numbers of observations and/or large numbers of variables, such as signal processing, speech recognition, neuroinformatics, and bioinformatics. Methods are commonly divided into linear and nonlinear approaches. Linear approaches can be further divided into feature selection and feature extraction. Dimensionality reduction can be used for noise reduction, data visualization, cluster analysis, or as an intermediate step to facilitat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Feature Selection
In machine learning, feature selection is the process of selecting a subset of relevant Feature (machine learning), features (variables, predictors) for use in model construction. Feature selection techniques are used for several reasons: * simplification of models to make them easier to interpret, * shorter training times, * to avoid the curse of dimensionality, * improve the compatibility of the data with a certain learning model class, * to encode inherent Symmetric space, symmetries present in the input space. The central premise when using feature selection is that data sometimes contains features that are ''redundant'' or ''irrelevant'', and can thus be removed without incurring much loss of information. Redundancy and irrelevance are two distinct notions, since one relevant feature may be redundant in the presence of another relevant feature with which it is strongly correlated. Feature extraction creates new features from functions of the original features, whereas feat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Outliers
In statistics, an outlier is a data point that differs significantly from other observations. An outlier may be due to a variability in the measurement, an indication of novel data, or it may be the result of experimental error; the latter are sometimes excluded from the data set. An outlier can be an indication of exciting possibility, but can also cause serious problems in statistical analyses. Outliers can occur by chance in any distribution, but they can indicate novel behaviour or structures in the data-set, measurement error, or that the population has a heavy-tailed distribution. In the case of measurement error, one wishes to discard them or use statistics that are robust to outliers, while in the case of heavy-tailed distributions, they indicate that the distribution has high skewness and that one should be very cautious in using tools or intuitions that assume a normal distribution. A frequent cause of outliers is a mixture of two distributions, which may be two d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
False Positives And False Negatives
A false positive is an error in binary classification in which a test result incorrectly indicates the presence of a condition (such as a disease when the disease is not present), while a false negative is the opposite error, where the test result incorrectly indicates the absence of a condition when it is actually present. These are the two kinds of errors in a binary test, in contrast to the two kinds of correct result (a and a ). They are also known in medicine as a false positive (or false negative) diagnosis, and in statistical classification as a false positive (or false negative) error. In statistical hypothesis testing, the analogous concepts are known as type I and type II errors, where a positive result corresponds to rejecting the null hypothesis, and a negative result corresponds to not rejecting the null hypothesis. The terms are often used interchangeably, but there are differences in detail and interpretation due to the differences between medical testing and st ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Association Rules
Association rule learning is a rule-based machine learning method for discovering interesting relations between variables in large databases. It is intended to identify strong rules discovered in databases using some measures of interestingness.Piatetsky-Shapiro, Gregory (1991), ''Discovery, analysis, and presentation of strong rules'', in Piatetsky-Shapiro, Gregory; and Frawley, William J.; eds., ''Knowledge Discovery in Databases'', AAAI/MIT Press, Cambridge, MA. In any given transaction with a variety of items, association rules are meant to discover the rules that determine how or why certain items are connected. Based on the concept of strong rules, Rakesh Agrawal, Tomasz Imieliński and Arun Swami introduced association rules for discovering regularities between products in large-scale transaction data recorded by point-of-sale (POS) systems in supermarkets. For example, the rule \ \Rightarrow \ found in the sales data of a supermarket would indicate that if a customer buy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Decision Tree
A decision tree is a decision support system, decision support recursive partitioning structure that uses a Tree (graph theory), tree-like Causal model, model of decisions and their possible consequences, including probability, chance event outcomes, resource costs, and utility. It is one way to display an algorithm that only contains conditional control statements. Decision trees are commonly used in operations research, specifically in decision analysis, to help identify a strategy most likely to reach a goal, but are also a popular tool in Decision tree learning, machine learning. Overview A decision tree is a flowchart-like structure in which each internal node represents a test on an attribute (e.g. whether a coin flip comes up heads or tails), each branch represents the outcome of the test, and each leaf node represents a class label (decision taken after computing all attributes). The paths from root to leaf represent classification rules. In decision analysis, a de ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Similarity Learning
Similarity learning is an area of supervised machine learning in artificial intelligence. It is closely related to regression and classification, but the goal is to learn a similarity function that measures how similar or related two objects are. It has applications in ranking, in recommendation systems, visual identity tracking, face verification, and speaker verification. Learning setup There are four common setups for similarity and metric distance learning. ; '' Regression similarity learning'' : In this setup, pairs of objects are given (x_i^1, x_i^2) together with a measure of their similarity y_i \in R . The goal is to learn a function that approximates f(x_i^1, x_i^2) \sim y_i for every new labeled triplet example (x_i^1, x_i^2, y_i). This is typically achieved by minimizing a regularized loss \min_W \sum_i loss(w;x_i^1, x_i^2,y_i) + reg(w). ; ''Classification similarity learning'' : Given are pairs of similar objects (x_i, x_i^+) and non similar objects (x_i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
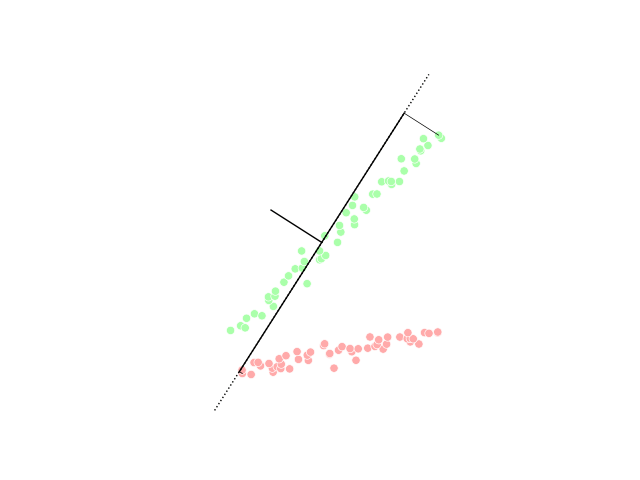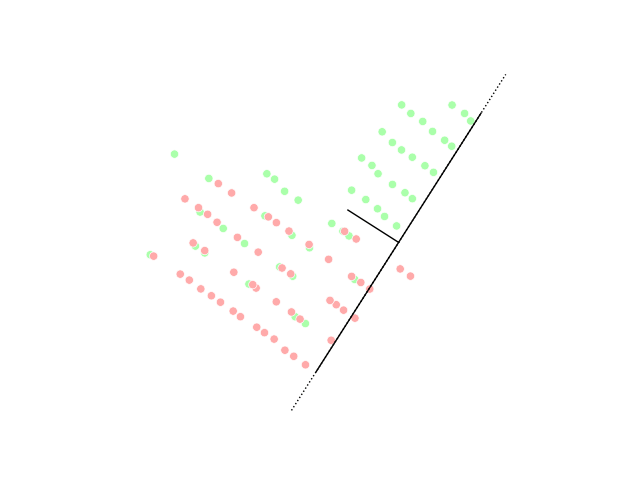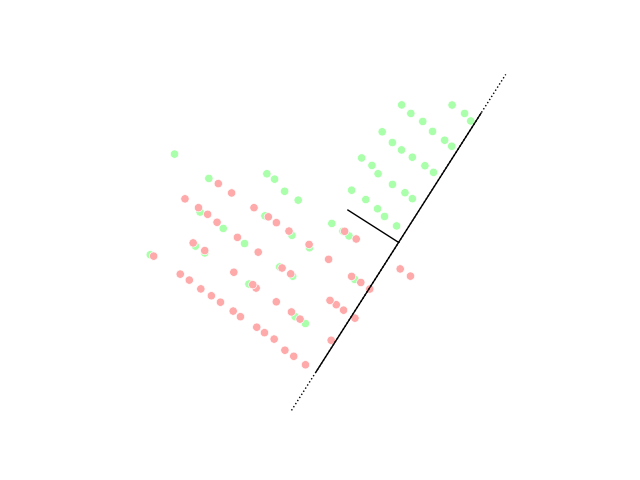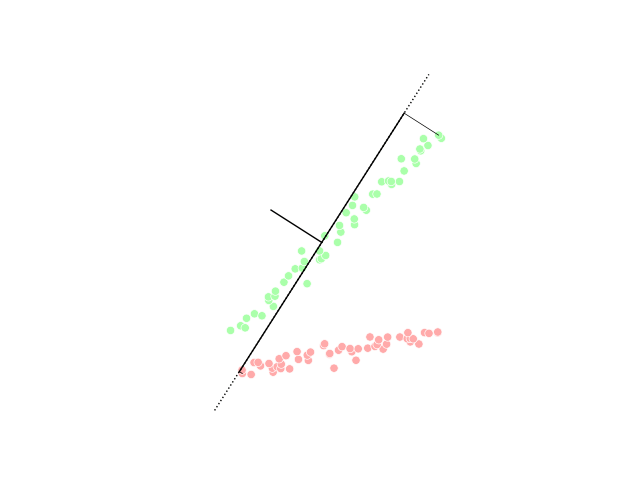
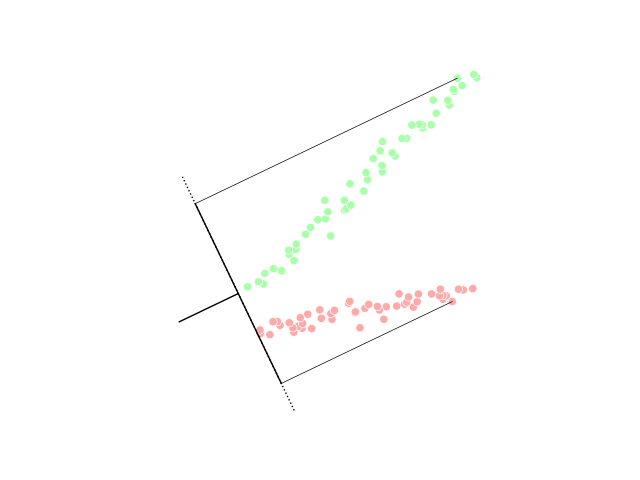
Linear Discriminant Analysis
Linear discriminant analysis (LDA), normal discriminant analysis (NDA), canonical variates analysis (CVA), or discriminant function analysis is a generalization of Fisher's linear discriminant, a method used in statistics and other fields, to find a linear combination of features that characterizes or separates two or more classes of objects or events. The resulting combination may be used as a linear classifier, or, more commonly, for dimensionality reduction before later statistical classification, classification. LDA is closely related to analysis of variance (ANOVA) and regression analysis, which also attempt to express one dependent variable as a linear combination of other features or measurements. However, ANOVA uses categorical variable, categorical independent variables and a continuous variable, continuous dependent variable, whereas discriminant analysis has continuous independent variables and a categorical dependent variable (''i.e.'' the class label). Logistic regr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |