|
List Of Coordinate Charts
This article contains a non-exhaustive list of coordinate charts for Riemannian manifolds and pseudo-Riemannian manifolds. Coordinate charts are mathematical objects of topological manifolds, and they have multiple applications in theoretical and applied mathematics. When a differentiable structure and a metric are defined, greater structure exists, and this allows the definition of constructs such as integration and geodesics. Charts for Riemannian and pseudo-Riemannian surfaces The following charts (with appropriate metric tensors) can be used in the stated classes of Riemannian and pseudo-Riemannian surfaces: See also * Coordinate chart *Coordinate system *Metric tensor * List of mathematics lists, particularly: ** List of multivariable calculus topics **List of Fourier analysis topics {{Short description, none This is a list of Fourier analysis topics. Fourier analysis * Multiplier (Fourier analysis) * Fourier shell correlation * Pinsky phenomenon Fourier series * Gener ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coordinate Charts
In mathematics, particularly topology, an atlas is a concept used to describe a manifold. An atlas consists of individual ''charts'' that, roughly speaking, describe individual regions of the manifold. In general, the notion of atlas underlies the formal definition of a manifold and related structures such as vector bundles and other fiber bundles. Charts The definition of an atlas depends on the notion of a ''chart''. A chart for a topological space ''M'' is a homeomorphism \varphi from an open subset ''U'' of ''M'' to an open subset of a Euclidean space. The chart is traditionally recorded as the ordered pair (U, \varphi). When a coordinate system is chosen in the Euclidean space, this defines coordinates on U: the coordinates of a point P of U are defined as the coordinates of \varphi(P). The pair formed by a chart and such a coordinate system is called a local coordinate system, coordinate chart, coordinate patch, coordinate map, or local frame. Formal definition of at ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
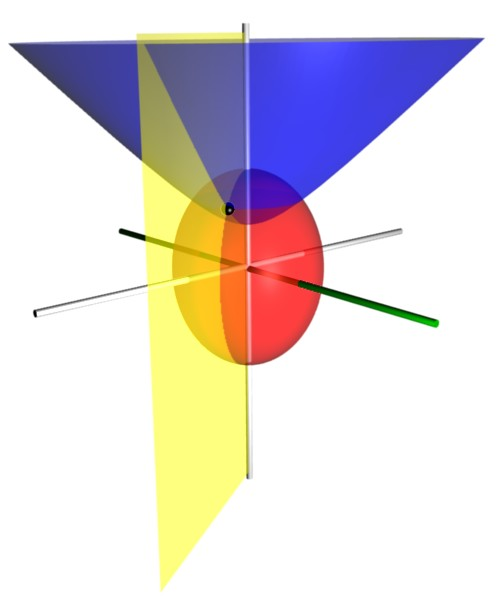
3-sphere
In mathematics, a hypersphere or 3-sphere is a 4-dimensional analogue of a sphere, and is the 3-dimensional n-sphere, ''n''-sphere. In 4-dimensional Euclidean space, it is the set of points equidistant from a fixed central point. The interior of a 3-sphere is a 4-ball. It is called a 3-sphere because topologically, the surface itself is 3-dimensional, even though it is curved into the 4th dimension. For example, when traveling on a 3-sphere, you can go north and south, east and west, or along a 3rd set of cardinal directions. This means that a 3-sphere is an example of a 3-manifold. Definition In coordinates, a 3-sphere with center and radius is the set of all points in real, Four-dimensional space, 4-dimensional space () such that :\sum_^3(x_i - C_i)^2 = ( x_0 - C_0 )^2 + ( x_1 - C_1 )^2 + ( x_2 - C_2 )^2+ ( x_3 - C_3 )^2 = r^2. The 3-sphere centered at the origin with radius 1 is called the unit 3-sphere and is usually denoted : :S^3 = \left\. It is often convenient to r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbolic Space
In mathematics, hyperbolic space of dimension ''n'' is the unique simply connected, ''n''-dimensional Riemannian manifold of constant sectional curvature equal to −1. It is homogeneous, and satisfies the stronger property of being a symmetric space. There are many ways to construct it as an open subset of \mathbb R^n with an explicitly written Riemannian metric; such constructions are referred to as models. Hyperbolic 2-space, H2, which was the first instance studied, is also called the hyperbolic plane. It is also sometimes referred to as Lobachevsky space or Bolyai–Lobachevsky space after the names of the author who first published on the topic of hyperbolic geometry. Sometimes the qualificative "real" is added to distinguish it from complex hyperbolic spaces. Hyperbolic space serves as the prototype of a Gromov hyperbolic space, which is a far-reaching notion including differential-geometric as well as more combinatorial spaces via a synthetic approach to negati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Toroidal Coordinates
Toroidal coordinates are a three-dimensional orthogonal coordinate system that results from rotating the two-dimensional bipolar coordinate system about the axis that separates its two foci. Thus, the two foci F_1 and F_2 in bipolar coordinates become a ring of radius a in the xy plane of the toroidal coordinate system; the z-axis is the axis of rotation. The focal ring is also known as the reference circle. Definition The most common definition of toroidal coordinates (\tau, \sigma, \phi) is : x = a \ \frac \cos \phi : y = a \ \frac \sin \phi : z = a \ \frac together with \mathrm(\sigma)=\mathrm(z). The \sigma coordinate of a point P equals the angle F_ P F_ and the \tau coordinate equals the natural logarithm of the ratio of the distances d_ and d_ to opposite sides of the focal ring : \tau = \ln \frac. The coordinate ranges are -\pi<\sigma\le\pi, and Coordinate surfaces Surfaces of c ...[...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Oblate Spheroidal Coordinates
Oblate spheroidal coordinates are a three-dimensional orthogonal coordinate system that results from rotating the two-dimensional elliptic coordinate system about the non-focal axis of the ellipse, i.e., the symmetry axis that separates the foci. Thus, the two foci are transformed into a ring of radius a in the ''x''-''y'' plane. (Rotation about the other axis produces prolate spheroidal coordinates.) Oblate spheroidal coordinates can also be considered as a limiting case of ellipsoidal coordinates in which the two largest semi-axes are equal in length. Oblate spheroidal coordinates are often useful in solving partial differential equations when the boundary conditions are defined on an oblate spheroid or a hyperboloid of revolution. For example, they played an important role in the calculation of the Perrin friction factors, which contributed to the awarding of the 1926 Nobel Prize in Physics to Jean Baptiste Perrin. These friction factors determine the rotational d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prolate Spheroidal Coordinates
Prolate spheroidal coordinates are a three-dimensional orthogonal coordinate system that results from rotating the two-dimensional elliptic coordinate system about the focal axis of the ellipse, i.e., the symmetry axis on which the foci are located. Rotation about the other axis produces oblate spheroidal coordinates. Prolate spheroidal coordinates can also be considered as a limiting case of ellipsoidal coordinates in which the two smallest principal axes are equal in length. Prolate spheroidal coordinates can be used to solve various partial differential equations in which the boundary conditions match its symmetry and shape, such as solving for a field produced by two centers, which are taken as the foci on the ''z''-axis. One example is solving for the wavefunction of an electron moving in the electromagnetic field of two positively charged nuclei, as in the hydrogen molecular ion, H2+. Another example is solving for the electric field generated by two small electrode ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbolic Coordinates
In mathematics, hyperbolic coordinates are a method of locating points in quadrant I of the Cartesian plane :\ = Q. Hyperbolic coordinates take values in the hyperbolic plane defined as: :HP = \. These coordinates in ''HP'' are useful for studying logarithmic comparisons of direct proportion in ''Q'' and measuring deviations from direct proportion. For (x,y) in Q take :u = \ln \sqrt and :v = \sqrt. The parameter ''u'' is the hyperbolic angle to (''x, y'') and ''v'' is the geometric mean of ''x'' and ''y''. The inverse mapping is :x = v e^u ,\quad y = v e^. The function Q \rarr HP is a continuous mapping, but not an analytic function. Alternative quadrant metric Since ''HP'' carries the metric space structure of the Poincaré half-plane model of hyperbolic geometry, the bijective correspondence Q \leftrightarrow HP brings this structure to ''Q''. It can be grasped using the notion of hyperbolic motions. Since geodesics in ''HP'' are semicircles with centers on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parabolic Coordinates
Parabolic coordinates are a two-dimensional orthogonal coordinate system in which the coordinate lines are confocal parabolas. A three-dimensional version of parabolic coordinates is obtained by rotating the two-dimensional system about the symmetry axis of the parabolas. Parabolic coordinates have found many applications, e.g., the treatment of the Stark effect and the potential theory of the edges. Two-dimensional parabolic coordinates Two-dimensional parabolic coordinates (\sigma, \tau) are defined by the equations, in terms of Cartesian coordinates: : x = \sigma \tau : y = \frac \left( \tau^ - \sigma^ \right) The curves of constant \sigma form confocal parabolae : 2y = \frac - \sigma^ that open upwards (i.e., towards +y), whereas the curves of constant \tau form confocal parabolae : 2y = -\frac + \tau^ that open downwards (i.e., towards -y). The foci of all these parabolae are located at the origin. The Cartesian coordinates x and y can be converted to para ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cylindrical Coordinate System
A cylindrical coordinate system is a three-dimensional coordinate system that specifies point positions around a main axis (a chosen directed line) and an auxiliary axis (a reference ray). The three cylindrical coordinates are: the point perpendicular distance from the main axis; the point signed distance ''z'' along the main axis from a chosen origin; and the plane angle of the point projection on a reference plane (passing through the origin and perpendicular to the main axis) The main axis is variously called the ''cylindrical'' or ''longitudinal'' axis. The auxiliary axis is called the ''polar axis'', which lies in the reference plane, starting at the origin, and pointing in the reference direction. Other directions perpendicular to the longitudinal axis are called ''radial lines''. The distance from the axis may be called the ''radial distance'' or ''radius'', while the angular coordinate is sometimes referred to as the ''angular position'' or as the ''azimuth''. The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Two-center Bipolar Coordinates
In mathematics, two-center bipolar coordinates is a coordinate system based on two coordinates which give distances from two fixed centers c_1 and c_2. This system is very useful in some scientific applications (e.g. calculating the electric field of a dipole on a plane). Transformation to Cartesian coordinates When the centers are at (+a, 0) and (-a, 0), the transformation to Cartesian coordinates (x, y) from two-center bipolar coordinates (r_1, r_2) is :x = \frac :y = \pm \frac\sqrt Transformation to polar coordinates When ''x'' > 0, the transformation to polar coordinates from two-center bipolar coordinates is :r = \sqrt :\theta = \arctan\left( \frac \right) where 2 a is the distance between the poles (coordinate system centers). Applications Polar plotters use two-center bipolar coordinates to describe the drawing paths required to draw a target image. See also * Bipolar coordinates *Biangular coordinates *Lemniscate of Bernoulli *Oval of Cassini *Cartesian oval *Ellipse ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Biangular Coordinates
In mathematics, biangular coordinates are a coordinate system for the plane where C_1 and C_2 are two fixed points, and the position of a point ''P'' not on the line \overline is determined by the angles \angle PC_1C_2 and \angle PC_2C_1. The sine rule can be used to convert from biangular coordinates to two-center bipolar coordinates. Applications Biangular coordinates can be used in geometric modelling and CAD. See also * Two-center bipolar coordinates In mathematics, two-center bipolar coordinates is a coordinate system based on two coordinates which give distances from two fixed centers c_1 and c_2. This system is very useful in some scientific applications (e.g. calculating the electric field ... * Bipolar coordinates * Sectrix of Maclaurin References External links G. B. M. Zerr Biangular Coordinates ''American Mathematical Monthly'' 17 (2), February 1910 J. C. L. Fish, ''Coordinates Of Elementary Surveying''George Shoobridge Carr, ''A synopsis of elementary resu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bipolar Coordinates
Bipolar coordinates are a two-dimensional orthogonal coordinates, orthogonal coordinate system based on the Apollonian circles.Eric W. Weisstein, Concise Encyclopedia of Mathematics CD-ROM, ''Bipolar Coordinates'', CD-ROM edition 1.0, May 20, 1999 There is also a third system, based on two poles (biangular coordinates). The term "bipolar" is further used on occasion to describe other curves having two singular points (foci), such as ellipses, hyperbolas, and Cassini ovals. However, the term ''bipolar coordinates'' is reserved for the coordinates described here, and never used for systems associated with those other curves, such as elliptic coordinates. Definition The system is based on two Focus (geometry), foci ''F''1 and ''F''2. Referring to the figure at right, the ''σ''-coordinate of a point ''P'' equals the angle ''F''1 ''P'' ''F''2, and the ''τ''-coordinate equals the natural logarithm of the ratio of the distances ''d''1 and ''d''2: : \tau = \ln \frac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |